深入浅出Transformer(一)

引言

Transformer的重要性不用多说了吧，NLP现在最火了两个模型——BERT和GPT，一个是基于它的编码器实现的，另一个是基于它的解码器实现的。

凡是我不能创造的，我都不能理解。

为了更好的理解Transformer¹模型，我们需要知道它的实现细节。本文我们就如庖丁解牛一般，剖析它的原理与实现细节——通过Pytorch实现。

为了更好的理解Transformer，英文阅读能力好的建议先看一下它的原始论文¹,以及两篇非常好的解释文章(这里和这里)。本文会结合这些文章的内容，争取阐述清楚每个知识点。由于内容有点多，可能会分成三篇文章。

为了方便，本文把原文的翻译结果也贴出来，翻译放到引用内。

背景

$这是原文翻译$ 循环神经网络，尤其是LSTM和GRU，一直以来都在序列建模和转导问题(比如语言模型和机器翻译)上保持统治地位。此后，人们不断努力提升循环网络语言模型和编码器-解码器结构的瓶颈。

循环模型通常是对输入和输出序列的符号位置进行因子计算。在计算期间对齐位置和时间步，基于前一时间步的隐藏状态$h_{t-1}$和当前时间步$t$的输入，循环生成了一系列隐藏状态$h_t$。这种固有的顺序特性排除了训练的并行化，这在更长的序列中成为重要问题，因为有限的内存限制了长样本的批次化。虽然最近有学者通过因子分解和条件计算技巧重大的提升了计算效率，同时提升了模型的表现。但是序列计算的基本限制仍然存在。

注意力机制已经变成了序列建模和各种任务中的转导模型的必备成分，允许为依赖建模而不必考虑输入和输出序列中的距离远近。除了少数情况外，这种注意力机制都与循环神经网路结合使用。

本文我们提出了Transformer，一个移除循环网络、完全基于注意力机制来为输入和输出的全局依赖建模的模型。Transformer 允许更多的并行化，并且翻译质量可以达到最牛逼水平，只需要在8个P100 GPU上训练12个小时。

模型架构

Transformer模型抛弃了RNN和CNN，是一个完全利用自注意去计算输入和输出的编码器-解码器模型。并且它还可以并行计算，同时计算效率也很高。

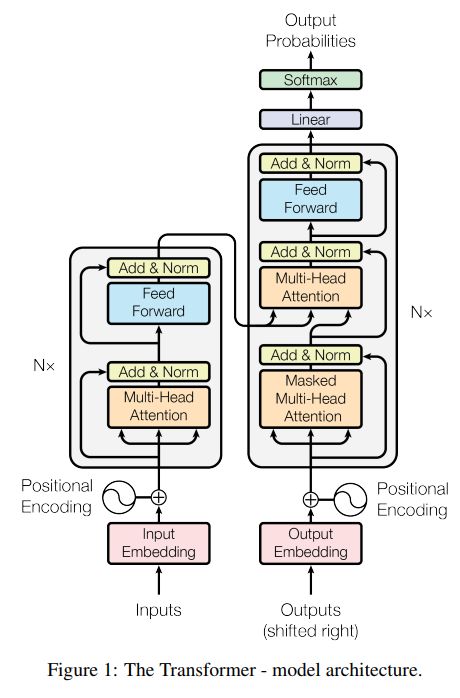
模型整体架构如图1所示。

大部分有竞争力的神经网络序列转导模型都有一个编码器-解码器(Encoder-Decoder)结构。编码器映射一个用符号表示的输入序列$(x_1,\cdots ,x_n)$到一个连续的序列表示$z=(z_1,\cdots ,z_n)$。给定$z$，解码器生成符号的一个输出序列$(y_1,\cdots ,y_m)$，一次生成一个元素。在每个时间步，模型是自回归(auto-regressive)的，在生成下个输出时消耗上一次生成的符号作为附加的输入。

Transformer沿用该结构并在编码器和解码器中都使用叠加的自注意和基于位置的全连接网络，分别对应图1左半部和右半部。

我们先来看左边编码器部分。

编码器

编码器是上图左边红色部分，解码器是上图右边蓝色部分。

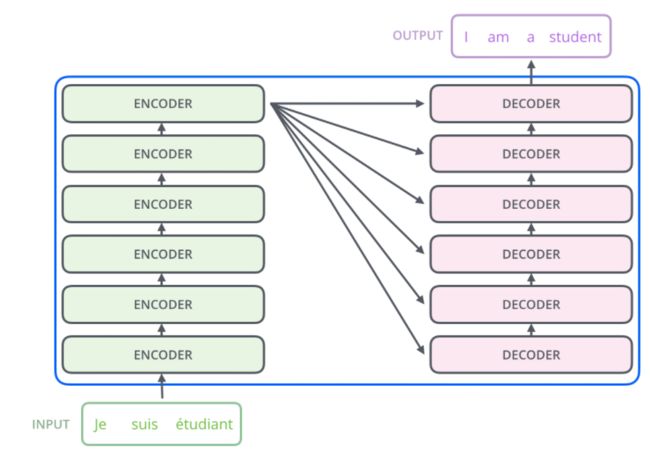
编码器： 编码器是由$N=6$个相同的层(参数独立)堆叠而成的。

上图中的$N\times$是叠加$N$次的意思，原文中编码器是由6个相同的层堆叠而成的。如下图所示：

低层编码器的输出作为上一层编码器的输入。

每层都有两个子层(sub-layer)，第一个子层是多头注意力层(Multi-Head Attention)，第二个是简单的基于位置的全连接前馈神经网络(positionwise fully connected feed-forward network)。

意思是每个编码器层都是由两个子层组成，第一个是论文中提出的多头注意力，这个比较重要，可以说是该篇论文的核心，理解了多头注意力整篇论文就理解的差不多了。后面会详细探讨。 经过多头注意力之后先进行残差连接，再做层归一化。

我们在两个子层周围先进行残差连接，然后进行层归一化(Layer Normalization)。这样，我们每个子层的输出是$LayerNorm(x+Sublayer(x))$，其中$Sublayer(x)$是子层自己实现的函数。为了利用残差连接，该模型中的所有子层和嵌入层，输出的维度都统一为$d_{model}=512$。

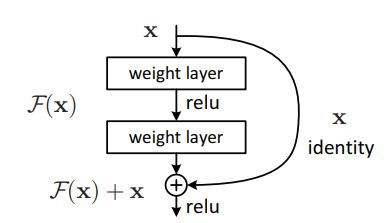
残差连接体现在上图的Add，层归一化就是上图的Norm。残差连接名字很唬人，其实原理非常简单，如下图：

假设网络中某层输入$x$后的输出为$F(x)$，不管激活函数是什么，经过深层网络都可能导致梯度消失的情况。增加残差连接，相当于某层输入$x$后的输出为$F(x)+x$。最坏的情况相当于没有经过$F(x)$这一层，直接输入到高层，这样高层的表现至少能和低层一样好。

而层归一化针对每个输入的每个维度进行归一化操作。假设有$H$个维度，$x=(x_1,x_2,\cdots ,x_H)$，层归一化首先计算这$H$个维度的均值和方差，然后进行归一化得到$N(x)$，接着做一个缩放，类似批归一化。

$$\mu =\frac{1}{H}\sum _{i=1}^H{x}_i,\sigma =\sqrt{\frac{1}{H}\sum _{i=1}^H(x_i-\mu {)}^2},N(x)=\frac{x-\mu }{\sigma },h=g\odot N(x)+b\text{\hspace{1em}(1)}$$
其中$h$就是LN层的输出，$\odot$是点乘操作，$\mu$和$\sigma$是输入各个维度的均值和方差，$g$和$b$是两个可学习的参数，和$h$的维度相同。

Transformer中输入的维度$H=512$。

下面我们通过Pytorch实现上面编码器中介绍的部分，Pytorch版的Transformer依据的是另一个神作²，也是一篇论文，里面完整的实现了Transformer。本文的实现也是根据这篇论文来的，他们的代码写得非常优雅，从可重用性和抽象性来看，体现了非常高的技术，值得仔细研究学习。

import numpy as np
import torch
import torch.nn as nn
import math, copy, time
from torch.autograd import Variable
import matplotlib.pyplot as plt
import seaborn # # seaborn在可视化self-attention的时候用的到
seaborn.set_context(context="talk") 

# 防止jupyter plt.show崩溃
import os    
os.environ['KMP_DUPLICATE_LIB_OK']='True'

首先导入所有需要的包。然后我们定义一个克隆函数，Transformer中多处用到了叠加，叠加就可以通过克隆来实现。

def clones(module, N):
    '''
    生成N个相同的层
    '''
    # 每个进行的都是深克隆
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])

ModuleList可以和Python普通列表一样进行索引，但是里面的模型会被合理的注册到网络中，这样里面模型的参数在梯度下降的时候进行更新。下面来看编码器的代码实现。

class Encoder(nn.Module):
    '''
    Encoder堆叠了N个相同的层，下层的输出当成上层的输入
    '''

    def __init__(self, layer, N):
        super(Encoder, self).__init__()

        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)

    def forward(self, x, mask):
        '''
        依次将输入和mask传递到每层
        :param x: [batch_size, input_len, emb_size]
        '''
        for layer in self.layers:
            # 下层的输出当成上层的输入
            x = layer(x, mask)
        # 最后进行层归一化
        return self.norm(x)

编码器的输入是前文中提到的子层(sub-layer)，因此这里克隆了$N$份子层，由于用的是深克隆，虽然模型是一模一样的，但是每个模型学到的参数肯定是不同的。

注意这里输入mask的作用，编码器输入mask一般是在进行批处理时，由于每个句子的长度可能不等，因此对于过短的句子，需要填充字符，一般用$0$表示，而这里的mask就能标出哪些字符为填充字符，这样可以不需要进行计算，以提高效率。

注意这里用到的的层归一化，是对整个编码器的输出进行层归一化，即在编码器最终结果输出到解码器之前，做的层归一化。

下面看一下层归一化LayerNorm的实现。

class LayerNorm(nn.Module):
    '''
    构建一个层归一化模块
    '''

    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        '''
        :param x: [batch_size, input_len, emb_size]
        '''
        # 计算最后一个维度的均值和方差
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2

我们注意输入$x$的维度，最后一个维度就是嵌入层的大小，我们就是对该维度进行归一化。这里还有一点需要补充的就是，层归一化要学习的参数只有两个，上文公式$(1)$中的$g$和$h$，这里分别对应$a_2$和$b_2$。所以通过nn.Parameter去构造这两个参数，这样这两个参数会出现在该模型的parameters()方法中，并且可以注册到模型中。

由于层数较深，为了防止模型过拟合，故增加了Dropout。

我们应用dropout到每个子层的输出，在它被加到子层的输入(残差连接)和层归一化之前。此外，我们将dropout应用于编码器和解码器栈中的嵌入和位置编码的和。对于基本模型，我们使用dropout比率为$P_{drop}=0.1$。

第一个应用Dropout的位置就是加入位置编码的词嵌入，后文会探讨。然后就是多头注意力层和全连接层的输出位置。

这里将上图中的Dropout、Add和Norm也设计成了一个模型(nn.Module)：

class SublayerConnection(nn.Module):
    '''
    残差连接然后接层归一化
    为了简化代码，先进行层归一化
    '''

    def __init__(self, size, dropout):
        '''
        :param size: 模型的维度，原文中统一为512
        :param dropout: Dropout的比率，原文中为0.1
        '''
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        '''
        应用残差连接到任何同样大小的子层
        '''
        return x + self.dropout(sublayer(self.norm(x)))

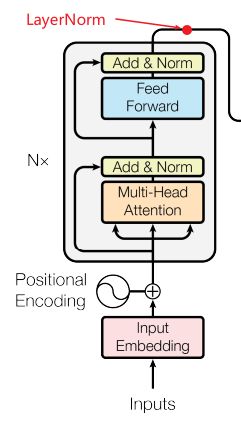
这样，我们个子层的输出是$LayerNorm(x+Sublayer(x))$，其中$Sublayer(x)$是一个子层自己实现的函数。我们对每个子层的输出应用Dropout ，在其添加到(高层)子层输入并进行层归一化之前。

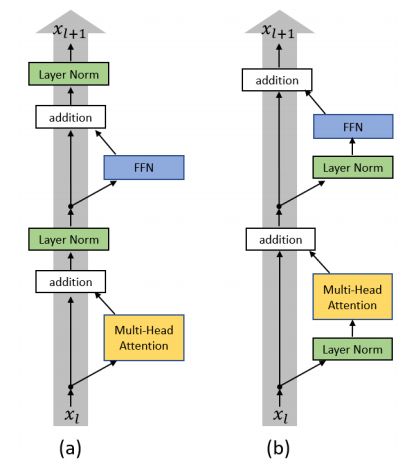
注意这里代码实现和原文中说的有点不同，主要是层归一化的位置，原文如上图$(a)$所示，叫Post-LN；这里的实现其实是上图$(b)$所示，叫做 Pre-LN。有人³ 证明Pre-LN这种方式效果更好。

我们知道编码器叠加了$N$层(EncoderLayer)，每层有两个子层，第一个是多头注意力层，第二个是一个简单的基于位置的全连接神经网络。

每个子层接了一个上面实现的SublayerConnection。

class EncoderLayer(nn.Module):
    '''
    编码器是由self-attention和FFN(全连接层神经网络)组成，其中self-attention和FNN分别用SublayerConnection封装
    '''

    def __init__(self, size, self_attn, feed_forward, dropout):
        '''
        :param: size: 模型的大小
        :param: self_attn: 注意力层
        :param: feed_forward: 全连接层
        '''
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn
        self.feed_forward = feed_forward
        # 编码器层共有两个子层
        self.sublayer = clones(SublayerConnection(size, dropout), 2) 
        self.size = size

    def forward(self, x, mask):
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
        return self.sublayer[1](x, self.feed_forward)

其中sublayer[0]就是第一个子层连接，其中封装了第一个子层，即多头注意力层，我们上面已经知道它会对立面的网络层的输出进行残差连接和Dropout等操作。这里的多头注意层通过lambda表达式调用了self.self_attn，因为注意力层有三个输入和一个mask。

然后输入到第二个子层连接，其中封装的是基于位置的全连接层。

下面我们开始触碰到核心部分——多头注意力层了。

注意力

注意力经NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE提出后就迅速应用到了各种Seq2Seq模型中，关于注意力可以参考这篇论文。这么经典的论文，博主也进行了翻译。

原文中用到的自注意力(self-attention)和经典的注意力机制中的注意力有点不同，具体我们来看一下。

给定自注意力层$n$个输入，就能产生$n$个输出。

自注意机制允许输入序列关注自己，来发现它们应该更关注自己的哪一部分。输出就是针对输入中每个单词的注意力得分。

以机器翻译任务为例，假设想翻译下面这段英文⁴。

”The animal didn't cross the street because it was too tired”(这个动物没有横穿街道，因为它太累了。)

上文中的它it指代什么？街道street还是动物animal，我们人类能很容易回答，因为我们知道只有动物才会累。

但是如何让算法知道这一点呢？答案就是自注意。

当模型处理单词it时，自注意让模型能关联it到animal。随着模型不断的处理每个单词(输入序列中的每个位置)，自注意允许模型查看输入序列中的其他位置来获得信息以更好地计算单词的注意力得分。

原文中通过一个注意力函数来计算注意力。

注意力函数可以说是匹配一个query和一系列key-value对到一个输出的函数。其中的query,key,value和输出都是向量。value的加权和得到输出，每个value的权重是通过一个query和相应key的某个函数计算。

这里query、key和value又是什么意思，翻译过来就是查询、键和值。可以理解为信息检索中的查询操作，如下图。假如我们输入“自然语言处理是什么”(少输入了一个是，不过不影响)。Key可以看成为每篇文章的标题，Value就是每篇文章的相关内容。

不过在自注意力中，Query/Key/Value都是根据同一个输入乘上不同的权重得到的。$这里说的是编码器中的注意力。如果是编码器-解码器之间的注意力，那么Key和Value来自编码器，Query来自解码器。$

计算自注意力的第一步就是，为编码器层的每个输入，都创建三个向量，分别是query向量，key向量和value向量。

正如我们上面所说，每个向量都是乘上一个权重矩阵得到的，这些权重矩阵是随模型一起训练的。

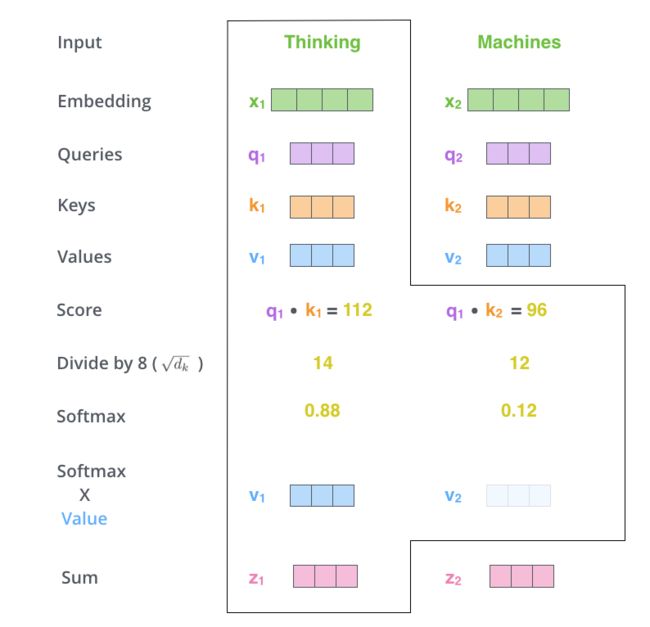
以上图的为例，假设输入“Thinking”、“Machines”两个单词，这个例子来自文章The Illustrated Transformer

我们发现将query、key和value分别用不同的、学到的线性映射$h$倍到$d_k$、$d_k$和$d_v$维效果更好，而不是用$d_{model}$维的query、key和value执行单个attention函数。 基于每个映射版本的query、key和value，我们并行执行attention函数，产生$d_v$维输出值。 将它们连接并再次映射，产生最终值。

这里的三个权重矩阵就是原文中说的三个线性映射，暂时忽略其中的$h$倍等描述。

进行线性映射的目的是转换向量的维度，转换成一个更小的维度。原文中是将$512$维转换为$64$维。

比如输入$x_1$乘以矩阵$W^Q$得到query向量$q_1$，然后乘以$W^k$和$W^V$分别得到key向量$k_1$和value向量$v_1$。

第二步 是计算注意力得分，假设我们想计算单词“Thinking”的注意力得分，我们需要对输入序列中的所有单词(包括自身)都进行某个操作。得到单词“Thinking”对于输入序列中每个单词的注意力得分，如果某个位置的得分越大，那么在生成编码时就越需要考虑这个位置。或者说注意力就是衡量$q$和$k$的相关性，相关性越大，那么在得到最终输出时，$k$对应的$v$在生成输出时贡献也越大。

那么这里所说的操作是什么呢？其实很简单，就是点乘。表示两个向量在多大程度上指向同一方向。类似余弦相似度，除了没有对向量的模进行归一化。

所以如果我们计算单词“Thinking”的注意力得分，需要计算$q_1$对$k_1$和$k_2$的点积。如上图所示。

第三步和第四步 是进行进行缩放，原文中是除以$\sqrt{d_k}=8$，然后经过softmax函数，使得每个得分都是正的，且总和为$1$。

经过Softmax之后的值就可以看成是一个权重了，也称为注意力权重。决定每个单词在生成这个位置的编码时能够共享多大程度。

第五步 用每个单词的value向量乘上对应的注意力权重。这一步用于保存我们想要注意单词的信息(给定一个很大的权重)，而抑制我们不关心的单词信息(给定一个很小的权重)。

第六步 累加第五步的结果，得到一个新的向量，也就是自注意力层在这个位置(这里是对于第一个单词“Thinking”来说)的输出。举一个极端的例子，假设某个单词的权重非常大，比如是$1$，其他单词都是$0$，那么这一步的输出就是该单词对应的value向量。

这就是计算第一个单词的自注意力输出完整过程。自注意力层的魅力在于，计算所有单词的输出可以通过矩阵运算一次完成。

我们把所有的输入编入一个矩阵$X$，上面的例子有两个输入，所以这里的$X$矩阵有两行。分别乘上权重矩阵$W^Q,W^K,W^V$就得到了$Q,K,V$向量矩阵。

然后除以$\sqrt{d_k}$进行缩放，再经过Softmax，得到注意力权重矩阵，接着乘以value向量矩阵$V$，就一次得到了所有单词的输出矩阵$Z$。

注意权重矩阵$W^Q,W^K,W^V$都是可以训练的，因此通过训练，可以为每个输入单词生成不同的注意力得分，从而得到不同的输出。

我们上面描述的就是论文中的下面内容，原文中称为缩放点乘注意力。

我们称我们这种特定的注意力为缩放点乘注意力(下图)。输入query和key的维度是$d_k$，value的维度是$d_v$。我们计算query和所有key的点乘结果，然后除以$\sqrt{d_k}$，最后应用一个softmax函数就得到value的相应权重。

在实践中，我们同时计算一组query的注意力函数，这一组query被压缩到一个矩阵$Q$，key和value也分别被压缩到矩阵$K$和$V$。我们通过下面的公式计算输出矩阵：
$$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V\text{\hspace{1em}(1)}$$
最常用的注意力函数是Bahdanau注意力，和点乘注意力。点乘注意力除了没有通过$\frac{1}{\sqrt{d_k}}$缩放外，和我们算法中的注意力函数相同。Bahdanau注意力通过一个单隐藏层的全连接网络计算。尽管这两个函数的复杂度都是相似的，但是点乘注意力在实际中更快、更节省空间。因为它能通过高度优化的矩阵乘法实现。

尽管在$d_k$值不大的情况下，两者性能差不多，Bahdanau注意力超过没有对大的$d_k$值缩放的点乘注意力，我们认为，对于大的$d_k$值，点乘的结果也变得非常大，导致softmax函数到极其小梯度的区域，为了防止这点，我们缩放点积结果到$\frac{1}{\sqrt{d_k}}$。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-z0rkLskC-1629439221919)(https://arxiv.org/pdf/1706.03762.pdf)]](https://gitee.com/nlp-greyfoss/images/raw/master/data/image-20210808161953963.png)

我们就可以得到注意力函数的实现：

def attention(query, key, value, mask=None, dropout=None):
    '''
    计算缩放点乘注意力
    :param query:  [batch_size, self.h, input_len, self.d_k]
    :param key:    [batch_size, self.h, input_len, self.d_k]
    :param value:  [batch_size, self.h, input_len, self.d_k]
    '''
    d_k = query.size(-1)
    # query: [batch_size, self.h, input_len, self.d_k]
    # key.transpose: [batch_size, self.h, self.d_k, input_len]
    # 此时就是批矩阵相乘 固定batch_size, self.h  -> input_len, self.d_k  x self.d_k, input_len = input_len, input_len
    # -> [batch_size, self.h, input_len, input_len]
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
    # 源序列也需要mask，因为批次内语句长短不一，对于短的语句，就需要填充字符
    if mask is not None:
        # 根据mask句子，把屏蔽的位置填-1e9，然后计算softmax的时候，-1e9的位置就被计算为0
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = torch.softmax(scores, dim=-1)  # 经过softmax得到注意力权重
    if dropout:
        p_attn = dropout(p_attn)
    #  [batch_size, self.h, input_len, input_len]  x  [batch_size, self.h, input_len, self.d_k]
    # -> [batch_size, self.h, input_len, self.d_k]
    return torch.matmul(p_attn, value), p_attn  # 返回最终的输出 和 注意力权重(可用户绘图)

至此，我们理解了注意力的计算。下面就来挑战多头注意力。

多头注意力

先来看下原文的描述。

我们发现将query、key和value分别用不同的、学到的线性映射$h$倍到$d_k$、$d_k$和$d_v$维效果更好，而不是用$d_{model}$维的query、key和value执行单个attention函数。 基于每个映射版本的query、key和value，我们并行执行attention函数，产生$d_v$维输出值。 将它们连接并再次映射，产生最终值，如下图所示。

多头注意力允许模型能对齐不同表示子空间信息到不同的位置。而普通的只有一个头的注意力会因为求平均而抑制了这一点。

$$\text{MultiHead}(Q,K,V)=\text{Concat}({\text{head}}_1,\cdots ,{\text{head}}_h)W^O$$
其中
$${\text{head}}_i=\text{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V),$$

参数矩阵$W_i^Q\in {\mathbb{R}}^{d_{\text{model}}\times d_k}$, $W_i^K\in {\mathbb{R}}^{d_{\text{model}}\times d_k}$, $W_i^V\in {\mathbb{R}}^{d_{\text{model}}\times d_v}$ and $W^O\in {\mathbb{R}}^{h{d}_v\times d_{\text{model}}}$。

在本文中，我们设置$h=8$个并行的注意力层，或注意力头。每个头中的$d_k=d_v=d_{\text{model}}/h=64$，由于每个头维度的减少，总的计算量和正常维度的单头注意力差不多($8\times 64=512$)。

多头的意思就是，同时计算多次自注意力，不过与原本的计算一次自注意力不同，计算多次注意力时的维度缩小为原来的$h$倍。原文中$h=8$，由于维度缩小$h$倍，意味着所需要的计算量也缩小为$h$倍，总共有$h$个头。最终总的计算量和不缩小维度的单头注意力差不多。

原来计算一次注意力，只能学到一种信息，现在我们对于同一位置计算8次注意力，可以理解为学到了8种关注信息。可能有的关注语义信息、有的关注句法信息等等。这样扩展了模型的表达能力。

注意，在Pytorch实现的时候，上图的$Q,K,V$其实都是输入$X$，对应的三个线性层，就是原文说的线性映射，原来是映射到$512$维，原文变成了映射成8个$64$维的$Q,K,V$向量矩阵。

⚡不要错误的认为多头注意力需要计算多次，牛逼的地方在于，仍然可以通过一次矩阵运算同时计算8个自注意力输出。

从上图可以看出，叠加了$h$个自注意力，每个都是独立运算的，最终把$h$个自注意力的输出连接(concat)在一起，变成一个矩阵，再经过一个线性变换，得到最终输出。

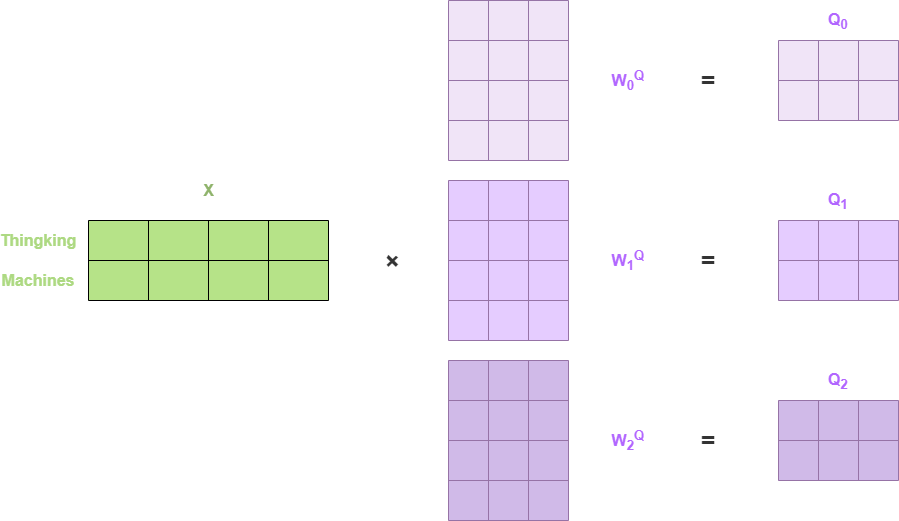
为了理解多头注意力，我们以$h=3$为例，让输入矩阵$X$乘以$W_0^Q,W_1^Q,W_2^Q$，分别得到$Q_0,Q_1,Q_2$，如下图：

来看一下维度，输入$X$的维度是$2\times 4$，表示有两个输入，词嵌入维度为$4$；

权重矩阵$W_0^Q,W_1^Q,W_2^Q$的维度都是$4\times 3$，表示把词嵌入维度由$4$进行线性变换，转换为$3$；

不同的$W^Q$权重矩阵，得到了不同的query向量矩阵$Q_0,Q_1,Q_2$，它们的维度是$2\times 3$。

上面的维度都很小，为了便于演示，实际上原文词嵌入+位置编码后的维度是$\ast \times 512$；

之前介绍的$W^Q,W^K,W^V$在多头注意力下，都变成了8个，即$W_i^Q,W_i^K,W_i^{V}i=1\cdots 8$。

那么多头注意力是如何通过矩阵运算一次计算多个注意力的输出呢？

第一步，把多个权重矩阵拼接起来，让输入$X$乘以权重矩阵，分别得到$Q,K,V$矩阵。

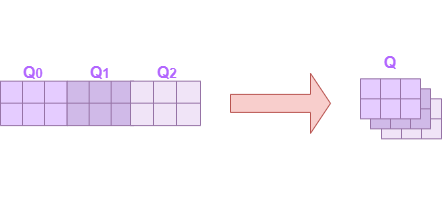
接下来通过矩阵的变形操作(reshape)，增加一个维度，变成叠加的三个query。

对于剩下的$K,V$都进行这样的操作，然后将变形后的$Q,K,V$输入到注意力函数中。

通过矩阵运算，得到叠加的$Z$矩阵，最终通过拼接(concat)操作，去掉增加的那个维度，然后再经过一个线性层，再次映射，得到最终输出。

class MultiHeadedAttention(nn.Module):
    '''
    多头注意力机制实现
    '''

    def __init__(self, h, d_model, dropout=0.1):
        '''
        输入维度和head数量h
        '''
        super(MultiHeadedAttention, self).__init__()

        assert d_model % h == 0
        # d_k是每个head的维度
        self.d_k = d_model // h
        self.h = h
        # 四个线性层，三个在输入端，一个在输出端
        # 在计算注意力之前先将query,key,value进行线性变换效果更好
        self.linears = clones(nn.Linear(d_model, d_model), 4)

        self.attn = None
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, query, key, value, mask=None):
        if mask is not None:
            # 同样的mask应用到所有h个head
            mask = mask.unsqueeze(1)
        n_batches = query.size(0)  # 批次大小

        # 1) 在批次内对query,key,value进行线性运算，分别转换成h个d_k维度的query,key,value：维度 d_model => h x d_k,
        # 对self.linears与(query,key,value)进行zip，相当于分别把query,key,value喂给前三个线性层，得到线性变换后的query,key,value
        # 如 query: [batch_size, input_len, d_model] -> 线性层 ->  [batch_size, input_len, d_model]
        # -> view -> [batch_size, input_len, self.h, self.d_k] -> transpose -> [batch_size, self.h, input_len, self.d_k]
        query, key, value = [l(x).view(n_batches, -1, self.h, self.d_k).transpose(1, 2)
                             for l, x in zip(self.linears, (query, key, value))]

        # 2) 对批次内所有线性变换后的向量调用注意力函数
        x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout)
        # 3) 通过view执行类似连接Z的操作，然后应用到最后一个线性层
        # view方法需要tensor是连续的，因此调用contiguous方法
        # x : [batch_size, self.h, input_len, self.d_k] -> transpose -> [batch_size, input_len, self.h, self.d_k]
        # -> view -> [batch_size, input_len, self.h*self.d_k]
        x = x.transpose(1, 2).contiguous().view(n_batches, -1, self.h * self.d_k)

        return self.linears[-1](x)

多头注意力的实现如上，输入接收query,key,value可以同时适用到解码器中。

我们模型中注意力机制的应用

Transformer以三种方式使用多头注意力：

1. 在编码器-解码器注意力层，query来自前一个解码器层，key和value来编码器输出。这允许解码器中每个位置能注意到输入序列中所有位置。这模仿了seq2seq模型中的典型的编码器-解码器的注意力机制。
2. 编码器中的自注意层。在自注意层中，所有的key,value和query都来自同一个地方，在这里是编码器中前一层的输出，编码器中每个位置都能注意到编码器前一层的所有位置。
3. 类似地，解码器中的自注意层允许解码器中的每个位置注意解码器中直到并包括该位置的所有位置。我们需要防止解码器中的左向信息流以保持自回归(auto-regressive)属性。我们在缩放点乘注意力中实现这点，通过屏蔽(mask)softmax的输入中所有不合法连接的值(设置为$-\infty$)。

基于位置的前馈网络

除了注意力子层，我们编码器和解码器中每个层都包含一个全连接前馈网络，它单独且相同地应用于每个位置。它包含了两个线性变换，其中有一个ReLU激活。
$$\text{FFN}(x)=\max (0,x{W}_1+b_1)W_2+b_2\text{\hspace{1em}(2)}$$
尽管线性变换对于不同位置来说是相同的，但每个子层中的参数都是不同的。还可以说是两个内核大小为1的卷积层。输入和输出的维度是$d_{model}=512$，内部层的维度$d_{ff}=2048$。

它的输入是所有位置的注意力向量，引入$FFN$的目的是转换注意力输出向量的表示空间，增加模型的表现能力，更好的作为下一个注意力层的输入。

class PositionWiseFeedForward(nn.Module):
    '''
    实现FFN网路
    '''

    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionWiseFeedForward, self).__init__()
        # 将输入转换为d_ff维度
        self.w_1 = nn.Linear(d_model, d_ff)
        # 将d_ff转换回d_model
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.w_2(self.dropout(torch.relu(self.w_1(x))))

至此编码器部分基本了解完毕了，除了

嵌入层

与其他序列转导模型类似，我们使用学习的嵌入层去转换输入和输出单词到$d_{model}$维的词向量。在嵌入层中，我们把它的权重乘了$\sqrt{d_{model}}$。

嵌入层比较简单。

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        self.lut = nn.Embedding(vocab, d_model)  # 词典大小 嵌入大小
        self.d_model = d_model

    def forward(self, x):
        '''
        x: [batch_size, input_len]
        '''
        # 把得到的词嵌入向量乘以sqrt(d_model)
        return self.lut(x) * math.sqrt(self.d_model)  # [batch_size, input_len, d_model]

位置编码

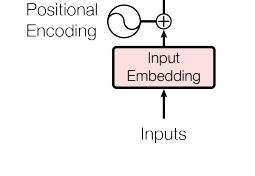
因为我们的模型不包含循环和卷积，为了使用序列顺序信息，我们必须接入一些关于序列中单词相对或绝对位置的信息 。为此，我们将位置编码添加到编码器和解码器栈底部的输入词嵌入中。位置编码和词嵌入有相同的维度$d_{model}$，所以它们可以求和。有多种位置编码可以选择，例如通过学习得到的和固定的位置编码。

我们使用不同频率的正弦和余弦函数来表示位置编码：
$$\begin{gathered} P{E}_{(pos,2i)}=\sin (pos/10000^{2i/d_{model}}) \\ P{E}_{(pos,2i+1)}=\cos (pos/10000^{2i/d_{model}}) \end{gathered}$$
其中$pos$表示位置，$i$表示维度。也就是说，位置编码的每个维度都对应一个正弦曲线。波长形成一个从$2\pi$到$10000\cdot 2\pi$的等比数列。我们之所以选择这个函数，是因为我们假设这个函数可以让模型很容易地学到相对位置的注意力，因为对于任何固定的偏移量$k$，$P{E}_{pos+k}$都能表示为$P{E}_{pos}$的一个线性函数。

我们也实验了学过的位置嵌入，然后发现这两种方式产生了几乎同样的结果。我们选择正弦版本是因为允许模型推断比训练期间遇到的更长的序列。

为了使用序列顺序信息，作者提出了利用不同频率的正弦和余弦函数表示位置编码。序列顺序信息重要性是不言而喻的。比如以下两个句子：

我爱你
你爱我

作者用词嵌入向量➕位置编码得到输入向量，这里简单解释一下为什么作者选用正弦和余弦函数。

假设我们自己设置位置编码，一个简单的办法是增加索引到词嵌入向量⁵。

假设$a$表示词嵌入向量。这种方法有一个很大的问题，即句子越长，后面单词的序号就越大，而且索引值过大，可能会掩盖了嵌入向量的“光辉”。

你说序号太大了，那么我把每个序号都除以句子长度总不大了吧。听起来不错，但是这引入了另一个问题，就是由于句子的长度不同，导致同样的值可能代表不同的意思，这样让我们的模型很困惑。比如$0.8$在句长为$5$的句子中表示第$4$个单词，但是在句长为$20$的句子中表示第$16$个单词。

因为我们上面句子长度为8，$2^3=8$，何不用二进制来表示顺序信息呢？如上图所示。从上往下看，比如4对应“100”，5对应“101”。

这里我们用3位表示就足够了，一般我们可以设置成$d_{model}$。

那这种方法就很好了吗？

1. 我们仍然没有完全归一化。我们想要位置编码也符合某种分布。最好让正负数的分布均匀，这个很好实现，可以通过函数$f(x)=2x-1$，将[0,1] -> [-1,1]
2. 我们的二进制向量来自离散函数，而不是连续函数的离散化。

我们的位置编码应该满足下面的要求⁶：

1. 对于每个时间步(句子中的单词位置)，它都能输出独一无二的编码
2. 任意两个时间步之间的距离都应该是一个常量，而不因句子长度而变
3. 我们的模型应该能轻易地泛化到更长的句子，它的值应该是有界的
4. 位置编码必须是确定的

作者提出的编码方式是一个简单且天才的技术，满足了上面所有的要求。首先，它不是一个标量，而是一个包含特定位置信息的$d$维向量。其次，该编码并没有整合到模型中。相反，这个向量用于为每个单词设置关于它在句子中位置的信息。换言之，通过注入单词的顺序来增强模型的输入。

令$t$为输入序列中某个位置，$\overrightarrow{p_t}$是该位置的位置编码，$d$是向量维度。$f$是通过以下公式产生位置编码向量的函数：
$${p_t}^{(i)}=f(t{)}^{(i)}:=\{\begin{array}{ll}\sin ({\omega }_k\cdot t),& \text{若}i=2k\\ \cos ({\omega }_k\cdot t),& \text{若}i=2k+1\end{array}$$
其中
$${\omega }_k=\frac{1}{10000^{2k/d}}$$
由该式子可以看出，频率是随着向量维度降低的(由$\frac{1}{2\pi }$降低成$\frac{1}{10000\cdot 2\pi }$)。因此波长形成一个从$2\pi$到$10000\cdot 2\pi$的等比数列。

我们也能想象位置编码$p_t$是一个包含各个频率的正弦和余弦向量，其中$d$可以被$2$整除。
$$p_t={\left[\begin{array}{c}\sin ({\omega }_1\cdot t)\\ \cos ({\omega }_1\cdot t)\\ \\ \sin ({\omega }_2\cdot t)\\ \cos ({\omega }_2\cdot t)\\ \\ ⋮\\ \\ \sin ({\omega }_{d/2}\cdot t)\\ \cos ({\omega }_{d/2}\cdot t)\end{array}\right]}_{d\times 1}$$
为什么正弦和余弦的组合可以表示顺序。假设我们用二进制来表示数字。
$$\begin{array}{rlr}0:\text{0}\text{0}\text{0}\text{0}& & 8:\text{1}\text{0}\text{0}\text{0}\\ 1:\text{0}\text{0}\text{0}\text{1}& & 9:\text{1}\text{0}\text{0}\text{1}\\ 2:\text{0}\text{0}\text{1}\text{0}& & 10:\text{1}\text{0}\text{1}\text{0}\\ 3:\text{0}\text{0}\text{1}\text{1}& & 11:\text{1}\text{0}\text{1}\text{1}\\ 4:\text{0}\text{1}\text{0}\text{0}& & 12:\text{1}\text{1}\text{0}\text{0}\\ 5:\text{0}\text{1}\text{0}\text{1}& & 13:\text{1}\text{1}\text{0}\text{1}\\ 6:\text{0}\text{1}\text{1}\text{0}& & 14:\text{1}\text{1}\text{1}\text{0}\\ 7:\text{0}\text{1}\text{1}\text{1}& & 15:\text{1}\text{1}\text{1}\text{1}\end{array}$$

可以看到，随着十进制数的增加，每个位的变化率是不一样的，越低位的变化越快，红色位$0$和$1$，每个数字都会变化一次；

而黄色位，每$8$个数字才会变化一次。

但是二进制值的$0,1$是离散的，浪费了它们之间无限的浮点数。所以我们使用它们的连续浮动版本-正弦函数。

此外，通过降低它们的频率，我们可以从红色位变成黄色位，这样就实现了这种低位到高位的变换。如下图所示：

下面补充一下波长和频率的计算：

对于正弦函数来说，波长(周期)的计算如上图。任意$\sin (Bx)$的波长是$\frac{2\pi }{B}$，频率是$\frac{B}{2\pi }$。

最后，通过设置位置编码的维度和词嵌入向量的维度一致，可以将位置编码加入到词向量。

原文中提到

对于任何固定的偏移量$k$，$P{E}_{pos+k}$都要能表示为$P{E}_{pos}$的一个线性函数。

上图顶部是长度为200、维度为150的序列转置后的位置矩阵$PE$，上图底部是所$p$在的位置向量中的第$i$个分量位置的正弦余弦函数图像，来自 Hands-on Machine Learning with Scikit Learn, Keras, TensorFlow: Concepts, Tools and Techniques to Build Intelligent Systems 2nd Edition

对每个频率${\omega }_k$相应的正-余弦对，存在一个线性转换$M\in {\mathbb{R}}^{2\times 2}$：
$$M.\left[\begin{array}{c}\sin ({\omega }_k\cdot t)\\ \cos ({\omega }_k\cdot t)\end{array}\right]=\left[\begin{array}{c}\sin ({\omega }_k\cdot (t+\varphi ))\\ \cos ({\omega }_k\cdot (t+\varphi ))\end{array}\right]$$

证明⁶：

假设$M$是一个$2\times 2$的矩阵，我们想要找到其中的元素$u_1,v_1,u_2,v_2$满足：
$$\left[\begin{array}{cc}{u}_1& v_1\\ u_2& v_2\end{array}\right]\cdot \left[\begin{array}{c}\sin ({\omega }_k\cdot t)\\ \cos ({\omega }_k\cdot t)\end{array}\right]=\left[\begin{array}{c}\sin ({\omega }_k\cdot (t+\varphi ))\\ \cos ({\omega }_k\cdot (t+\varphi ))\end{array}\right]$$
利用三角函数两角和的正弦公式和余弦公式，得到：

$$\left[\begin{array}{cc}{u}_1& v_1\\ u_2& v_2\end{array}\right]\cdot \left[\begin{array}{c}\sin ({\omega }_k\cdot t)\\ \cos ({\omega }_k\cdot t)\end{array}\right]=\left[\begin{array}{c}\sin ({\omega }_k\cdot t)\cos ({\omega }_k\cdot \varphi )+\cos ({\omega }_k\cdot t)\sin ({\omega }_k\cdot \varphi )\\ \cos ({\omega }_k\cdot t)\cos ({\omega }_k\cdot \varphi )-\sin ({\omega }_k\cdot t)\sin ({\omega }_k\cdot \varphi )\end{array}\right]$$
得到下面两个等式：
$$\begin{array}{rl}{u}_1\sin ({\omega }_k\cdot t)+v_1\cos ({\omega }_k\cdot t)=& \cos ({\omega }_k\cdot \varphi )\sin ({\omega }_k\cdot t)+\sin ({\omega }_k\cdot \varphi )\cos ({\omega }_k\cdot t)\\ u_2\sin ({\omega }_k\cdot t)+v_2\cos ({\omega }_k\cdot t)=& -\sin ({\omega }_k\cdot \varphi )\sin ({\omega }_k\cdot t)+\cos ({\omega }_k\cdot \varphi )\cos ({\omega }_k\cdot t)\end{array}$$
相应的，可得：
$$\begin{array}{rl}{u}_1=\cos ({\omega }_k.\varphi )& v_1=\sin ({\omega }_k.\varphi )\\ u_2=-\sin ({\omega }_k.\varphi )& v_2=\cos ({\omega }_k.\varphi )\end{array}$$
所以，就得到了最终的矩阵$M$为：
$$M_{\varphi ,k}=\left[\begin{array}{cc}\cos ({\omega }_k\cdot \varphi )& \sin ({\omega }_k\cdot \varphi )\\ -\sin ({\omega }_k\cdot \varphi )& \cos ({\omega }_k\cdot \varphi )\end{array}\right]$$
从上可以看出，最终的转换与$t$无关。

类似地，我们可以找到其他正-余弦对的$M$，最终允许我们表示$p_{t+\varphi }$为一个$p_t$对任意固定偏移量$\varphi$的线性函数。这个属性，使模型很容易学得相对位置信息。

这解释了为什么要选择交替的正弦和余弦函数，仅通过正弦或余弦函数达不到这一点。

我们实现位置编码如下：

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)  # 注册为一个缓存，但是不是模型的参数，默认随模型其他参数一起保存

    def forward(self, x):
        x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
        return self.dropout(x)

参考

---

1. Attention Is All You Need ↩︎ ↩︎

2. The Annotated Transformer ↩︎

3. On Layer Normalization in the Transformer Architecture ↩︎

4. The Illustrated Transformer ↩︎

5. Master Positional Encoding ↩︎

6. Transformer Architecture: The Positional Encoding ↩︎ ↩︎