项目一 Part 4.2 基于网格搜索的超参数优化实战
【Kaggle】Telco Customer Churn 电信用户流失预测案例
第四部分导读
在案例的第二、三部分中,我们详细介绍了关于特征工程的各项技术,特征工程技术按照大类来分可以分为数据预处理、特征衍生、特征筛选三部分,其中特征预处理的目的是为了将数据集整理、清洗到可以建模的程度,具体技术包括缺失值处理、异常值处理、数据重编码等,是建模之前必须对数据进行的处理和操作;而特征衍生和特征筛选则更像是一类优化手段,能够帮助模型突破当前数据集建模的效果上界。并且我们在第二部分完整详细的介绍机器学习可解释性模型的训练、优化和解释方法,也就是逻辑回归和决策树模型。并且此前我们也一直以这两种算法为主,来进行各个部分的模型测试。
而第四部分,我们将开始介绍集成学习的训练和优化的实战技巧,尽管从可解释性角度来说,集成学习的可解释性并不如逻辑回归和决策树,但在大多数建模场景下,集成学习都将获得一个更好的预测结果,这也是目前效果优先的建模场景下最常使用的算法。
总的来说,本部分内容只有一个目标,那就是借助各类优化方法,抵达每个主流集成学习的效果上界。换而言之,本部分我们将围绕单模优化策略展开详细的探讨,涉及到的具体集成学习包括随机森林、XGBoost、LightGBM、和CatBoost等目前最主流的集成学习算法,而具体的优化策略则包括超参数优化器的使用、特征衍生和筛选方法的使用、单模型自融合方法的使用,这些优化方法也是截至目前,提升单模效果最前沿、最有效、同时也是最复杂的方法。其中有很多较为艰深的理论,也有很多是经验之谈,但无论如何,我们希望能够围绕当前数据集,让每个集成学习算法优化到极限。值得注意的是,在这个过程中,我们会将此前介绍的特征衍生和特征筛选视作是一种模型优化方法,衍生和筛选的效果,一律以模型的最终结果来进行评定。而围绕集成学习进行海量特征衍生和筛选,也才是特征衍生和筛选技术能发挥巨大价值的主战场。
而在抵达了单模的极限后,我们就会进入到下一阶段,也就是模型融合阶段。需要知道的是,只有单模的效果到达了极限,进一步的多模型融合、甚至多层融合,才是有意义的,才是有效果的。
Part 4.集成算法的训练与优化技巧
# 基础数据科学运算库
import numpy as np
import pandas as pd
# 可视化库
import seaborn as sns
import matplotlib.pyplot as plt
# 时间模块
import time
import warnings
warnings.filterwarnings('ignore')
# sklearn库
# 数据预处理
from sklearn import preprocessing
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OrdinalEncoder
from sklearn.preprocessing import OneHotEncoder
# 实用函数
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score, roc_auc_score
from sklearn.model_selection import train_test_split
# 常用评估器
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
# 网格搜索
from sklearn.model_selection import GridSearchCV
# 自定义评估器支持模块
from sklearn.base import BaseEstimator, TransformerMixin
# 自定义模块
from telcoFunc import *
# 导入特征衍生模块
import features_creation as fc
from features_creation import *
# re模块相关
import inspect, re
# 其他模块
from tqdm import tqdm
import gc
然后执行Part 1中的数据清洗相关工作:
# 读取数据
tcc = pd.read_csv('WA_Fn-UseC_-Telco-Customer-Churn.csv')
# 标注连续/离散字段
# 离散字段
category_cols = ['gender', 'SeniorCitizen', 'Partner', 'Dependents',
'PhoneService', 'MultipleLines', 'InternetService', 'OnlineSecurity', 'OnlineBackup',
'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies', 'Contract', 'PaperlessBilling',
'PaymentMethod']
# 连续字段
numeric_cols = ['tenure', 'MonthlyCharges', 'TotalCharges']
# 标签
target = 'Churn'
# ID列
ID_col = 'customerID'
# 验证是否划分能完全
assert len(category_cols) + len(numeric_cols) + 2 == tcc.shape[1]
# 连续字段转化
tcc['TotalCharges']= tcc['TotalCharges'].apply(lambda x: x if x!= ' ' else np.nan).astype(float)
tcc['MonthlyCharges'] = tcc['MonthlyCharges'].astype(float)
# 缺失值填补
tcc['TotalCharges'] = tcc['TotalCharges'].fillna(0)
# 标签值手动转化
tcc['Churn'].replace(to_replace='Yes', value=1, inplace=True)
tcc['Churn'].replace(to_replace='No', value=0, inplace=True)
features = tcc.drop(columns=[ID_col, target]).copy()
labels = tcc['Churn'].copy()
同时,创建自然编码后的数据集以及经过时序特征衍生的数据集:
# 划分训练集和测试集
train, test = train_test_split(tcc, random_state=22)
X_train = train.drop(columns=[ID_col, target]).copy()
X_test = test.drop(columns=[ID_col, target]).copy()
y_train = train['Churn'].copy()
y_test = test['Churn'].copy()
X_train_seq = pd.DataFrame()
X_test_seq = pd.DataFrame()
# 年份衍生
X_train_seq['tenure_year'] = ((72 - X_train['tenure']) // 12) + 2014
X_test_seq['tenure_year'] = ((72 - X_test['tenure']) // 12) + 2014
# 月份衍生
X_train_seq['tenure_month'] = (72 - X_train['tenure']) % 12 + 1
X_test_seq['tenure_month'] = (72 - X_test['tenure']) % 12 + 1
# 季度衍生
X_train_seq['tenure_quarter'] = ((X_train_seq['tenure_month']-1) // 3) + 1
X_test_seq['tenure_quarter'] = ((X_test_seq['tenure_month']-1) // 3) + 1
# 独热编码
enc = preprocessing.OneHotEncoder()
enc.fit(X_train_seq)
seq_new = list(X_train_seq.columns)
# 创建带有列名称的独热编码之后的df
X_train_seq = pd.DataFrame(enc.transform(X_train_seq).toarray(),
columns = cate_colName(enc, seq_new, drop=None))
X_test_seq = pd.DataFrame(enc.transform(X_test_seq).toarray(),
columns = cate_colName(enc, seq_new, drop=None))
# 调整index
X_train_seq.index = X_train.index
X_test_seq.index = X_test.index
ord_enc = OrdinalEncoder()
ord_enc.fit(X_train[category_cols])
X_train_OE = pd.DataFrame(ord_enc.transform(X_train[category_cols]), columns=category_cols)
X_train_OE.index = X_train.index
X_train_OE = pd.concat([X_train_OE, X_train[numeric_cols]], axis=1)
X_test_OE = pd.DataFrame(ord_enc.transform(X_test[category_cols]), columns=category_cols)
X_test_OE.index = X_test.index
X_test_OE = pd.concat([X_test_OE, X_test[numeric_cols]], axis=1)
Ch.2 基于网格搜索的超参数优化实战
在完成了特征衍生与初步筛选后,接下来就将进入到模型训练与优化的阶段了,正如此前所说,对特征的更精确的筛选其本质也可以看成是一种优化方法。不过需要注意的是,一般在特征初筛结束后,我们都将围绕当前筛选出来的特征尝试进行模型训练,若模型能够有效的挖掘出当前特征池的全部信息,且计算量在可以承受的范围内,则无需进一步进行特征精筛;但如果模型无法有效挖掘当前海量特征的全部信息,甚至是出现了加入新特征的模型效果反而不如只带入原始特征的模型的情况,则需要考虑进一步围绕特征进行更加精确的搜索,以提高模型效果。
而要如何才能测试模型能否“消化”当前海量特征池的全部信息呢?很明显,只靠此前介绍的可解释型模型(逻辑回归和决策树模型)肯定是远远不够的,这里我们将采用可解释型更弱、但更能从海量特征池中提取有效信息的集成学习进行建模。并且也将采用模型融合的策略,以进一步提升模型效果和从海量特征中提取有效信息的能力。集成学习+模型融合,这也是效果优先的机器学习建模必然会采用的策略。
本节我们先聚焦如何训练并优化好一个集成学习算法,再考虑带入衍生特征后模型的优化方法。这里需要注意,少量特征和海量特征在优化策略方面也会有较大的差别,我们将逐步深入进行介绍。
- 随机森林+网格搜索策略
不过不同于逻辑回归和决策树模型,集成学习的超参数设置与优化会更加复杂。一般来说不同优化器会适用于不同集成算法的超参数空间。关于集成学习的基本原理、超参数解释以及各类不同优化器的基本原理,在此前的课程中都有详细介绍,本节作为实战阶段的内容,将更加注重介绍优化器的实战使用技巧。本节我们将首先介绍一个最基础、但同时也是效果非常好的一套集成学习建模+优化策略,即随机森林模型+网格搜索优化器。
随机森林作为Bagging算法中的集大成者,一直以来都是建模效果最好、适用面最广的集成学习之一,哪怕是在XGBoost、LightGBM和CatBoost这些后起之秀面前,RF也毫不逊色,在很多情况下,RF也是值得甚至是必须尝试的模型。同时,在多模型融合、甚至是多层多模型融合当道的今天,学会针对第一梯队的全部集成学习算法进行训练和调优,就成了所有算法工作人员的必修课。因此本节我们将先从RF开始,介绍集成学习超参数搜索与优化技巧。
- 网格搜索优化器
而具体到要使用哪种优化器对随机森林进行超参数调优,一般来说肯定是首选网格搜索。其一是因为随机森林的超参数几乎全部都是离散变量,网格搜索完全能够胜任;其二则是这套策略从建模到调优,都可以借助sklearn来完成,无需额外的数据格式转化,同时模型评估器和超参数评估器接口一致,调用起来也会非常方便。当然,对于网格搜索评估器来说,不仅可以应用于随机森林,同时也可以其他很多集成学习的优化,甚至在当下,不同优化器匹配不同集成学习,都成了模型融合提升效果的一种手段。总而言之,数量使用网格搜索进行超参数优化,也是算法工作人员的必修课。
- sklearn中网格搜索评估器
目前来说sklearn中超参数优化器有四种,分别是GridSearchCV(网格搜索)、RandomizedSearchCV(随机网格搜索)、HalvingSearchCV(对半网格搜索)和HalvingRandomizedSearchCV(对半随机网格搜索)。其中网格搜索是通过枚举搜索出一组最优超参数,枚举的精度最高但效率最低,也就是网格搜索其实是精度最高的搜索算法,但往往伴随着巨大的计算量;而加入了随机网格搜索,则是随机选取了原始参数空间的子空间,然后在这个子空间内进行枚举,尽管还是枚举,但由于参数空间的缩小,计算量也会随之减少,并且伴随着这个参数子空间不断扩大(可人工修改参数),随机网格搜索的计算量和精度都将逼近网格搜索,简而言之随机网格搜索是一种牺牲精度换效率的搜索方式;相比随机网格搜索,对半网格搜索采用了类似锦标赛的筛选机制进行多轮的参数搜索,每一轮输入原始数据一部分数据进行模型训练,并且剔除一半的备选超参数。由于每一轮都只输入了一部分数据,因此不同备选超参数组的评估可能存在一定的误差,但由于每一轮都只剔除一半的超参数组而不是直接选出最优的超参数组,因此也拥有一定的容错性。不难发现,这个过程也像极了RFE过程——每一轮用一个精度不是最高的模型剔除一个最不重要的特征,即保证了执行效率、同时又保证了执行精度。
如果从一个宏观视角来看,随机网格搜索是通过减少备选参数组来减少计算量,而对半网格搜索则是减少带入的数据量,来减少计算量。二者其实都能一定程度提升超参数的搜索效率,但也存在损失精度的风险。当然,如果还想更进一步提高搜索效率,则可以考虑对半搜索和随机搜索的组合——对半随机网格搜索,这种搜索策略实际上就是对半搜索的思路+随机网格搜索的超参数空间,即在一个超参数子空间内进行多轮筛选,每一轮剔除一半的备选超参数组。这种方法的搜索效率是最高的,但同时精度也相对较差。
因此,到底选择哪种优化器,实际上还是一个效率和效果平衡的问题。一般来说,首先方案肯定是采用网格搜索进行超参数优化,但不建议设置太大的超参数搜索空间,而是配合人工经验每次设置一个相对较小的参数空间,然后逐步调整、甚至是分参数分批进行搜索,以提高整个搜索效率;而只有当单独一组超参数的训练都非常耗时时,才会考虑使用其他两种超参数搜索方法。
若要深究随机网格搜索和对半网格搜索哪个误差更大,则要看情况而定。简单来说,如果超参数空间内,最优超参数组附近存在多个且效果和最优超参数组相近的次优超参数组,则随机网格搜索效果会更好,因为在随机抽样时很有可能抽中次优超参数组;但如果最优超参数组的效果比次优超参数组效果好很多,则对半网格搜索效果会更好,因为此时最优超参数组因为效果拔群,所以哪怕是少量样本,也会更容易脱颖而出。
本节我们就将围绕当前数据集来进行网格搜索评估器的实战演练,并通过这个过程快速获取参数设置与超参数搜索的经验,如何用好网格搜索评估器进行参数调优,也是所有模型训练进阶的必修课。
- 原始数据不调参
在进行超参数搜索调参之前,我们先简单测试不进行调优时的模型训练结果:
from sklearn.ensemble import RandomForestClassifier
start = time.time()
RF = RandomForestClassifier(n_jobs=15, random_state=12).fit(X_train_OE, y_train)
print(time.time()-start)
#0.12277936935424805
RF.score(X_train_OE, y_train), RF.score(X_test_OE, y_test)
#(0.9977281332828474, 0.7756956274843839)
RF.n_estimators
#100
能够发现,在不进行超参数优化时,模型存在明显的过拟合倾向,当然这也是很多集成算法在应对简单数据集时会表现出的一般状况。同时单独模型在小量样本下训练速度较快,在构建100棵树的情况下仅用时0.12s。当然,我们也可以进一步查看当前模型对特征的利用率:
RF.feature_importances_
# array([0.02812245, 0.01974651, 0.02421983, 0.01963431, 0.00603235,
# 0.0223819 , 0.02811445, 0.05395741, 0.02698412, 0.02560977,
# 0.04127569, 0.01718816, 0.01773947, 0.07040168, 0.02639826,
# 0.05104428, 0.15185081, 0.17836349, 0.19093506])
(RF.feature_importances_ == 0).sum()
#0
能够看到,此时并不存在特征重要性为0的特征,即模型在训练过程中用到了全部19个特征,模型利用率比单独树模型更高。当然我们也可以从模型的其他参数观察模型的特征利用效率,在不调参的情况下,随机森林的max_features(每棵树分配到的最多特征)为auto,即特征总数开二次方,即4-5个特征,而总共建了100棵树,每棵树又没有剪枝,自然在极大概率情况下每个特征都会被用到:
RF.max_features
#'auto'
np.sqrt(19)
#4.358898943540674
注意这几个参数,后面将围绕这几个参数来估计模型调参时的运行时间及模型对特征的利用效率。
一、网格搜索调参实战技巧
接下来我们尝试进行网格搜索调参,并在这个过程中介绍网格搜索调参的实战技巧。
1.确定调优参数
首先肯定是要先确定调哪些参数,也就是需要确定模型的参数空间的维度。随机森林参数众多,但不是每个参数都对模型结果有影响,并且有些参数彼此之间是存在关联关系的,调整其中一个或者几个即可,带入太多无关参数会使得参数空间过大、极大程度影响搜索效率。这里回顾随机森林参数如下:
| Name | Description |
|---|---|
| n_estimators | 决策树模型个数 |
| criterion | 规则评估指标或损失函数,默认基尼系数,可选信息熵 |
| splitter | 树模型生长方式,默认以损失函数取值减少最快方式生长,可选随机根据某条件进行划分 |
| max_depth | 树的最大生长深度,类似max_iter,即总共迭代几次 |
| min_samples_split | 内部节点再划分所需最小样本数 |
| min_samples_leaf | 叶节点包含最少样本数 |
| min_weight_fraction_leaf | 叶节点所需最小权重和 |
| max_features | 在进行切分时候最多带入多少个特征进行划分规则挑选 |
| random_state | 随机数种子 |
| max_leaf_nodes | 叶节点最大个数 |
| min_impurity_decrease | 数据集再划分至少需要降低的损失值 |
| bootstrap | 是否进行自助抽样 |
| oob_score | 是否输出袋外数据的测试结果 |
| min_impurity_split | 数据集再划分所需最低不纯度,将在0.25版本中移除 |
| class_weight | 各类样本权重 |
| ccp_alpha | 决策树限制剪枝参数,相当于风险项系数 |
| max_samples | 进行自助抽样时每棵树分到的样本量 |
随机森林的参数整体可以分为两个大类,其一是单独一颗树的剪枝参数,包括splitter、max_depth、min_samples_split、min_samples_leaf、min_weight_fraction_leaf、max_leaf_nodes、min_impurity_decrease、ccp_alpha等,从树模型的理论上来看,这些参数统一可以由ccp_alpha一个参数代替,但随机森林是由多棵树构成,我们无法单独针对每棵树设置一个ccp_alpha,并且由于sklearn的决策树计算流程和CART树的原理存在一定差异,因此ccp_alpha参数实际剪枝效果并不明显。在单独决策树的剪枝参数中,核心参数有以下四个,分别是min_samples_leaf、min_samples_split、max_leaf_nodes和max_depth,这四个参数的组合效果基本就能够完全决定单独一个决策树的剪枝结果,若有余力,可考虑围绕剩余参数进行搜索。
决策树的其他参数优化效果并不显著,另一个原因也是因为其他参数都是连续型变量,而网格搜索对连续型变量的最优值搜索效果并不好,而且通过枚举的方法搜索连续变量也将耗费非常大的计算量。
而第二类参数则是随机森林的集成类参数,包括n_estimators、bootstrap、max_features、max_samples、oob_score等,对于随机森林来说,自助抽抽样是提升Bagging效果的重要手段,因此bootstrap需要设置为True,并且max_samples需要参与搜索,而由于网格搜索中并不会用到oob_score,因此该参数可以设置为False。而在其他参数中,n_estimators和max_features两个参数也是影响模型效果的重要参数,需要进行搜索。
此外需要注意的是,如果样本偏态非常明显,并且最终模型是以Recall或者F1-Score作为评估指标,则可以考虑带入class_weight进行搜索。
另外,关于随机数种子random_state,一般来说对于大样本而言,影响并不明显,而如果是小样本,则会有一定程度影响。Telco数据集是相对较小的数据集,但并不建议对random_state进行搜索,其一是random_state其实是一个无限的搜索空间、并且没有任何取值规律可言,最重要的一点,在下一小节我们将介绍关于模型“自融合”的方法,通过该方法输出的模型融合结果,也将极大程度减少random_state对最终预测结果的影响。
总结一下,针对当前数据集,我们需要围绕就min_samples_leaf、min_samples_split、max_leaf_nodes、max_depth、max_samples、n_estimators、max_features七个参数进行搜索调优。
2.设计参数空间时面临的“舍罕王赏麦”问题
“传说国际象棋的发明者是古印度的西萨·班·达依尔。那时的国王是舍罕,世人称为舍罕王。国王想奖励他便问宰相需要得到什么赏赐。宰相开口说道:“请您在棋盘的第一个格子上放1粒麦子,第二个格子上放2粒,第三个格子上放4粒,第四个格子放8粒…即每一个次序在后的格子上放的麦粒必须是前一个格子麦粒数的倍数,直到最后一个格子即第64格放满为止,这样我就十分满足了。”国王哈哈大笑,慷慨地答应了宰相的这个谦卑的请求。这位聪明的宰相到底要求的是多少麦粒呢?” --《舍罕王赏麦》
按照这个指数级增长的结果,宰相的要求实际上是 2 64 − 1 2^{64}-1 264−1粒大米,相当于当时全世界在2000年内所产小麦的总和。
在确定了要调优哪些参数后,接下来就需要确定每个参数的搜索空间了,这一步也是直接关系到参数搜索效率的关键步骤。首先我们需要对参数搜索需要耗费的时间有基本的判断,才好进行进一步搜索策略的制定,否则极容易出现“仿佛永远等不到搜索停止”的情况出现。
首先需要明确的是,参数空间内总备选参数组合的数量为各参数取值之积,且随着参数空间内每个参数取值增加而呈现指数级上升,且随着参数空间内参数维度增加(增加新的超参数)呈指数级上升,且二者呈现叠加效应。例如现有参数空间如下:
# 参数空间有4个备选参数组合
parameter_space0 = {"min_samples_leaf": range(1, 3),
"min_samples_split": range(1, 3)
}
则备选的参数组合有 2 ∗ 2 = 4 2*2=4 2∗2=4个。而此时如果调整"min_samples_leaf": range(1, 4),则备选参数组合就变成了 2 ∗ 3 = 6 2*3=6 2∗3=6个,也就是说,"min_samples_leaf"参数搜索范围增加1,造成的搜索次数增加了两次,而非一次。
# 参数空间有6个备选参数组合
parameter_space1 = {"min_samples_leaf": range(1, 4),
"min_samples_split": range(1, 3)
}
并且,如果我们新增一个超参数维度"max_depth": range(1, 4),则目前总共的备选参数组合就达到了 2 ∗ 3 ∗ 3 = 18 2*3*3=18 2∗3∗3=18个,也就是说,增加"min_samples_split"3个数值,造成的搜索次数增加了18-6=12次,而非3次:
# 参数空间有18个备选参数组合
parameter_space2 = {"min_samples_leaf": range(1, 4),
"min_samples_split": range(1, 3),
"max_depth": range(1, 4)
}
当然,这种指数级的变化在少量数据情况下可能无法看出“真正的威力”,但如果参数稍微多些或计算过程稍微复杂些,例如假设parameter_space1搜索任务耗时5分钟,而在只增加了一个参数及3个不同取值的情况下,parameter_space2就将耗费15分钟。而如果更复杂些,不是5*3=15分钟,而是15*3=45分钟呢,甚至是1小时*3=3小时呢,参数空间的略微扩大就可能造成搜索时间的指数级增加。
此外,在进行网格搜索时,每一次建模背后还存在5折交叉验证,也就是需要训练5次模型,而每一次随机森林的建模,都伴随着几十个甚至是上百个决策树模型训练,背后的计算量可想而知。
介于此,在参数空间设计时就会有这样一个核心问题,那就是参数空间设置小了不确定最优参数是否在这个空间内,参数空间设置大了又不确定何时能算完。这也就是所谓的参数空间设计时面临的“舍罕王赏麦”问题。
舍罕王赏麦后续:国王哪有这么多麦子呢?他的一句慷慨之言,成了他欠宰相西萨·班·达依尔的一笔永远也无法还清的债。正当国王一筹莫展之际,王太子的数学老师知道了这件事,他笑着对国王说:“陛下,这个问题很简单啊,就像1+1=2一样容易,您怎么会被它难倒?”国王大怒:“难道你要我把全世界所有的小麦都给他?”年轻的教师说:“没有必要啊,陛下,其实,您只要让宰相大人到粮仓去,自己数出那些麦子就可以了,假如宰相大人一秒钟数一粒,数完所有的麦子所需要的时间,大约是5800亿年,就算宰相大人日夜不停地数,数到他魂归极乐,也只是数出那些麦粒中极小的一部分,这样的话,就不是陛下无法支付赏赐,而是宰相大人自己没有能力取走赏赐。”国王恍然大悟,当下就召来宰相,将教师的方法告诉了他。西萨·班·达依尔沉思片刻后笑道:“陛下啊,您的智慧超过了我,那些赏赐,我也只好不要了!”
3.超参数搜索的“凸函数”假设
如何解决这个问题,最好的解决方案是“小步迭代、快速调整”。在介绍这种方案之前,要先介绍在超参数调优时大家都会默认的一个假设,那就是超参数的取值和模型效果往往呈现严格“凸函数”的特性,例如假设参数"min_samples_leaf"在取值为5时模型效果最好,那么在参数取值为1、2、3、4时,模型效果是依次递增的,而如果参数取值为6、7、8,则模型效果是依次递减的,因此如果我们设计的该参数的搜索空间是"min_samples_leaf": range(6, 9),参数在6、7、8之间取值,则最优结果将会是min_samples_leaf=6,即预设的参数空间的下届,此时我们就需要进一步的移动参数空间,例如改为"min_samples_leaf": range(5, 8),即让参数在5、6、7之间取值,很明显,最终输出的挑选结果将会是min_samples_leaf=5,但此时仍然是搜索空间的下届,因此我们还需要进一步移动搜索空间,即移动至"min_samples_leaf": range(4, 7),即让参数在4、5、6之间取值,此时输出的最优结果将会是min_samples_leaf=5,此时就无需再移动超参数空间了,因为此时的参数空间已经包括了“凸函数”的最小值点,再往左边移动没有任何意义,这个过程如下图所示:
对于单个参数来说,如果呈现出搜索空间包含了最优值点(或者最优值点不在搜索空间的边界上)时,则判断已经找到了最优超参数。
如果超参数的取值不仅是数值,而是数值和其他类型对象混合的情况,则其他类型对象需要单独作为一个备选项参与搜索。
对于单个变量是如此,对于多个变量来说也是如此,若最终超参数搜索结果呈以下状态,则说明我们已经找到了一组最优超参数组:
当然,这种“凸函数假设”其实并没有充份严谨的理论依据,更多的是人们长期实践总结出来的结论。
4.小步前进,快速调整
接下来我们来看如何通过“小步迭代快速调整”的方法来进行超参数的搜索。在这个策略里,我们每次需要设置一个相对较小的参数搜索空间,然后快速执行一次超参数搜索,并根据超参数搜索结果来调整参数空间,并进行更进一步的超参数搜索,如此往复,直到参数空间内包含了全部参数的最优解为止。就像此前举例的那样,我们不会给"min_samples_leaf"一次设置一个非常大的参数搜索范围(如[1,9]),而是每次设置一个更小的搜索范围,通过不断调整这个范围来定位最优解。
既然要反复执行搜索任务,就必然需要一定程度控制单次搜索任务所需要的时间。当然,单次搜索的时间会和CPU、数据量、参数空间大小有关,但一般来说,对于小样本,单次搜索任务最好控制在5-30min内,而对于海量样本,最好也控制在30min-2H内,特殊情况可以适当放宽单次搜索任务的时间。
不过无论单次搜索任务耗时或长或短,我们都需要首先有个大概的预判,即本次搜索需要多久,方便我们确定“下次回来看结果”的时间。这里我们以Telco原始数据集为例,来简单测试单次搜索任务需要的时间。这里我们先测试最短单次搜索需要耗费的时间,由于我们需要让每个最优参数落在某个区间的中间,因此每个超参数的取值范围区间至少包含三个数值,例如"min_samples_leaf": range(4, 7)、该参数本次搜索至少有三个备选值,此外,如果有些参数包含非数值型参数,则需要在数值参数区间基础上再加上一个非数值型参数,例如"max_samples":[None, 0.6, 0.5, 0.4]。
5.首次搜索时超参数取值范围的经验依据
接下来介绍首次搜索时超参数取值范围的经验依据,也就是在第一次设置超参数搜索空间时,随机森林模型推荐的超参数取值范围。我们知道,从理论上来说,每个超参数都有可能有非常多个备选的取值,例如min_samples_leaf,就可以在1到样本总数之间取任意值,但实际上根据长期模型优化的结果来看,大多数情况下min_samples_leaf的最优取值都是在2到10之间,因此min_samples_leaf的初始三个取值可以设置为range(1, 10, 3),也就是[1, 4, 7]。
list(range(1, 10, 3))
#[1, 4, 7]
并且在这次搜索过程中,如果出现最优取值为4,则说明最优取值在4附近,下一轮就可以设置为[3, 4, 5],进一步确定最优取值。类似的情况还有min_samples_split。而max_depth的取值范围一般在5到20之间,超过20层的树往往都是过拟合的模型,而如果本身数据量较小,max_depth的最优取值一般不会超过15,因此max_depth的初始搜索范围可以设置为range(5, 16, 5),即[5, 10, 15]。
list(range(5, 16, 5))
#[5, 10, 15]
而max_features的参数范围设置会跟样本特征数量有关。我们知道,在默认情况下max_features=‘auto’,假设样本总共有m个特征,每个决策树将分配 m \sqrt{m} m个特征,max_features备选参数为log2,即每个决策树将分配 l o g 2 m log_2{m} log2m个特征。一般来说max_features的最优解会落在[ l o g 2 m log_2{m} log2m*50%, m \sqrt{m} m*150%]范围内,假设现在有100个特征,则max_features的最优值经验范围为:
np.log2(100) * 0.5
#3.321928094887362
np.sqrt(100) * 1.5
#15.0
即[3, 15]之间,但需要注意的是,除了搜索具体的数值外,还需要加上sqrt和log2两个参数,因此,对于一个包含了100个特征的数据集来说,我们可以设置如下max_features初始参数搜索范围:
['sqrt', 'log2'] + list(range(3, 15, 3))
#['sqrt', 'log2', 3, 6, 9, 12]
对于随机森林来说,max_features参数也可以设置为0到1之间的浮点数,此时就是按比例设置带入特征。出于更精准的角度考虑,最好是搜索到带入多少个特征,而不是带入百分之多少特征。另外,百分比实际上也是连续变量,正如此前所说,对连续变量进行网格搜索,也会产生较大误差。
接下来是n_estimators,树模型总数,这是一个变动很大的参数,总的来说会和特征彼此之间的相似程度有关,特征彼此之间相似度越高、n_estimators取值就越小,反之n_estimators取值就越大,当然n_estimators也会一定程度受到样本数量影响。但综合来看,n_estimators基本是在10到200之间取值,如果样本数量较少(例如样本数量不足1万条),则n_estimators会在10到150之间取值。本数据集实际上属于样本数量较少的数据集,因此n_estimators基本会在10到150之间取值,我们可以设置如下初步搜索范围:
list(range(10, 160, 70))
#[10, 80, 150]
对于最优值高度不确定的超参数,我们往往会设置一个较大的初始搜索超参数空间,但代价就是往往可能需要更多轮的搜索才能确定最优超参数。
接下来是max_leaf_nodes,该参数默认情况下为None,也就是不限制叶节点个数,该参数会受到树深度、每棵树接受到的数据量有关,一般来说max_leaf_nodes的数值往往在20到100之间,而对于小样本数据集,max_leaf_nodes初始范围建议设置在20到70之间:
[None] + list(range(20, 70, 20))
#[None, 20, 40, 60]
max_samples的默认参数同样也是None,即每棵决策树都接受和原始样本数量相同的样本量,和max_features一样,max_samples也支持输入整数对象和浮点数对象,输入整数对象时表示具体带入多少条数据,而输入浮点数对象时,则表示每棵树接收样本数量占总样本比例。对于大部分模型来说,将max_samples调到0.5以下(也就是输入50%的样本)才会有模型提升效果,因此初始情况下建议设置如下参数组:
[None, 0.4, 0.5, 0.6]
#[None, 0.4, 0.5, 0.6]
先确定一个大概的最优比例,然后再搜索具体带入多少条样本的样本数。例如假设总共是100条样本,第一轮搜索结果是max_samples=0.4,则接下来可以继续搜索[35, 40, 45],进一步缩小范围,并最终搜索到一个更加精准的数值。
总结一下,随机森林需要搜索的7个参数及其第一轮搜索时建议的参数空间如下:
| params | 经验最优范围 |
|---|---|
| min_samples_leaf | [1, 4, 7]; range(1, 10, 3) |
| min_samples_split | [1, 4, 7]; range(1, 10, 3) |
| max_depth | [5, 10, 15]; range(5, 16, 5) |
| max_leaf_nodes | [None, 20, 40, 60]; [None] + list(range(20, 70, 20)) |
| n_estimators | [10, 80, 150]; range(10, 160, 70) |
| max_features | [‘sqrt’, ‘log2’] +[ l o g 2 ( m ) log_2{(m)} log2(m)*50%, m \sqrt{m} m*150%] 其中m为特征数量 |
| max_samples | [None, 0.4, 0.5, 0.6] |
在设置了初始参数后,接下来就是一轮轮搜索与调整了,我们需要大致掌握每一次搜索任务所需要耗费的时间,然后在每次搜索任务结束时及时回到电脑前,准备设置调整参数空间并进行下一次搜索。
6.超参数之间的交叉影响
并且需要注意的是,在进行超参数搜索时,超参数彼此之间是存在交叉影响的,因此如果某次搜索只带入了部分参数进行搜索,那么如果后续增加了其他参数,则再次搜索时这些超参数的最优值也会发生变化。例如某次搜索超参数A在[1,2,3]中取值,找到了最优值A=2,现在如果继续加入超参数B,同时搜索A在[1,2,3]和B在[2,3,4]中最优取值组合,则极有可能出现A的最优取值变成了A=3,此时就要移动A的取值范围了(最优值落在了边界上),接下来如果继续加入超参数C、超参数D、超参数E等,每次加入一个都需要重新搜索一次,这个过程就会变得非常麻烦。当然,需要注意的是,如果只有A和B两个超参数,那么确实可以先搜索A、再搜索B,因为在两个超参数的情况下,二者相互影响有限,单独围绕A搜索出来的最优值2,在加入超参数B之后,A的最优值极有可能仍然在2附近变动,此时我们可以以2为中心设置搜索范围,之前搜索出来的A=2的最优值结果,在同时搜索A和B时仍然具有参考价值。但如果后续加入了C、D、E等更多的超参数,由于超参数彼此之间相互影响也会呈现指数级变动,因此极有可能后续A的取值会偏离2较远,有可能会变成10、20甚至是30,此时反观最开始搜索出来的A=2的最优值,对后续A的搜索过程就变得毫无价值了。
因此,受此启发,一般来说如果超参数个数较多,则可以分两批、甚至是分三批进行搜索,例如有A、B、C、D、E五个超参数时,可以先搜索A、B、C,在搜索出一组最优值后,再以此为中心创建搜索空间并加入新的D、E两个参数,设置各自对应的搜索空间,并进行第二批搜索。基本过程如下:
总之,最终一定要得到一个全部超参数每个最优点都在给定区间范围内的结果。
此外,正如此前所说,如果算力有限或者经过尝试发现以此搜索任务耗费时间过长,则可以将所有的参数分两批进行搜索,对于上述这七个参数来说,我们可以先围绕彼此关联度较为紧密的min_samples_leaf、min_samples_split、max_depth、max_leaf_nodes和n_estimators五个参数进行搜索,然后再加入max_features和max_samples进行搜索。
二、随机森林网格搜索调参实战
在有了网格搜索优化技巧的基础知识储备后,接下来我们围绕Telco原生数据集来进行随机森林网格搜索实战。一方面测试在原始数据集情况下随机森林模型超参数优化的最好结果,同时我们也将用过一个实例来具体观察我们制定的“小步迭代、快速调整”的调优策略是否能真的帮助我们高效快速的确定最优超参数。
1.设置初始参数空间与第一轮搜索
- 首轮搜索
首先,根据此前介绍,设置初始参数空间并进行搜索,同时计算本次运行的时间。原始数据集总共有19条特征,开方运算与log2计算结果如下:
np.sqrt(19)
#4.358898943540674
np.sqrt(19) * 1.5
#6.538348415311011
np.log2(19) * 0.5
#2.1239637567217926
此时max_features可以设置参数如下:
['sqrt', 'log2'] + list(range(2, 7, 2))
#['sqrt', 'log2', 2, 4, 6]
据此可执行第一轮搜索如下:
start = time.time()
# 设置超参数空间
parameter_space = {
"min_samples_leaf": range(1, 10, 3),
"min_samples_split": range(1, 10, 3),
"max_depth": range(5, 16, 5),
"max_leaf_nodes": [None] + list(range(20, 70, 20)),
"n_estimators": range(10, 160, 70),
"max_features":['sqrt', 'log2'] + list(range(2, 7, 2)),
"max_samples":[None, 0.4, 0.5, 0.6]}
# 实例化模型与评估器
RF_0 = RandomForestClassifier(random_state=12)
grid_RF_0 = GridSearchCV(RF_0, parameter_space, n_jobs=15)
# 模型训练
grid_RF_0.fit(X_train_OE, y_train)
print(time.time()-start)
#226.55377650260925
- 计算运行时间与参数空间
第一轮搜索在五折交叉验证的条件下,总共搜索了6480组参数:
3 * 3 * 3 * 4 * 3 * 5 * 4
#6480
且在n_jobs=15的情况下,本次搜索任务总耗时226.5s,约4分钟:
226.55377650260925 / 60
#3.7758962750434875
约0.035s完成一组超参数的计算。
226.55377650260925 / 6480
#0.034962002546698956
需要注意的是,这里的运行时间只能作为参考,并不是一个绝对的运行时间。在很多情况下,小段代码的运行时间会受到很多因素影响,包括硬件条件(对于机器学习来说主要是CPU和内存)、是否是首次运行代码等,都会对代码运行时间有较大影响。
- 查看运行结果
然后查看当前情况下模型预测结果:
grid_RF_0.best_score_
#0.8084053639517215
grid_RF_0.score(X_train_OE, y_train), grid_RF_0.score(X_test_OE, y_test)
#(0.8517606967057932, 0.7847813742191937)
能够看出,在进行第一轮超参数搜索时,模型结果的过拟合倾向已经得到了有效抑制,并且对比此前逻辑回归最终的优化结果,目前模型已经得到了一个较好的结果了:
| Models | CV.best_score_ | train_score | test_score |
|---|---|---|---|
| Logistic+grid | 0.8045 | 0.8055 | 0.7932 |
| RF+grid_R1 | 0.8084 | 0.8517 | 0.7848 |
最后,重点关注本轮搜索得出的超参数最优取值:
grid_RF_0.best_params_
# {'max_depth': 10,
# 'max_features': 'sqrt',
# 'max_leaf_nodes': None,
# 'max_samples': 0.4,
# 'min_samples_leaf': 1,
# 'min_samples_split': 7,
# 'n_estimators': 80}
并据此设置下一轮搜索策略:
- max_depth本轮最优取值为10,而原定搜索空间为[5, 10, 15],因此第二轮搜索时就可以以10为中心,缩小步长,进行更精准的搜索;
- max_features本轮最优取值为sqrt,说明最优解极有可能在4附近,因此第二轮搜索时可以设置一组更加精准的在4附近的数值,搭配sqrt参数一起进行搜索;
- max_leaf_nodes本轮最优取值为None,则有可能说明上一轮给出的其他备选数值不够激进,下一轮搜索时可以在一个更大的区间范围内设置备选数值;
- max_samples本轮最优取值为0.4,下一轮可以以0.4为中心,设置一组跨度更小、精度更高的取值进行搜索;
- min_samples_leaf本轮最优取值为1,下一轮可以设置range(1, 4)进行搜索(参数不能取得比1更小的值);
- min_samples_split本轮最优取值为7,下一轮可以以7为中心,设置更小的范围进行搜索;
- n_estimators本轮最优取值为80,下一轮可以以80为中心,设置更小的范围进行搜索,但需要注意的是,上一轮n_estimators取值搜索的跨度为70,下轮搜索时可以缩减到10。
2.第二轮搜索
根据调整策略,重新设置超参数空间,开始第二轮搜索:
start = time.time()
# 设置超参数空间
parameter_space = {
"min_samples_leaf": range(1, 4),
"min_samples_split": range(6, 9),
"max_depth": range(9, 12),
"max_leaf_nodes": [None] + list(range(10, 100, 30)),
"n_estimators": range(70, 100, 10),
"max_features":['sqrt'] + list(range(2, 5)),
"max_samples":[None, 0.35, 0.4, 0.45]}
# 实例化模型与评估器
RF_0 = RandomForestClassifier(random_state=12)
grid_RF_0 = GridSearchCV(RF_0, parameter_space, n_jobs=15)
# 模型训练
grid_RF_0.fit(X_train_OE, y_train)
print(time.time()-start)
#235.17643809318542
2.1 计算运行时间与参数空间
第二轮搜索时对参数空间范围控制的仍然很好,整体来看每个参数的数值设置都在一个比较范围内,最终计算了5184组参数:
3 * 3 * 3 * 4 * 3 * 4 * 4
#5184
实际运行时间仍然为4分钟:
235.17643809318542/60
#3.9196073015530906
235.17643809318542 / 5184
#0.045365825249457065
约0.05s完成一组超参数搜索。
2.2 查看运行结果
接下来查看模型运行结果:
grid_RF_0.best_score_
#0.808785226914366
grid_RF_0.score(X_train_OE, y_train), grid_RF_0.score(X_test_OE, y_test)
#(0.8458917076864824, 0.7921635434412265)
| Models | CV.best_score_ | train_score | test_score |
|---|---|---|---|
| Logistic+grid | 0.8045 | 0.8055 | 0.7932 |
| RF+grid_R1 | 0.8084 | 0.8517 | 0.7848 |
| RF+grid_R2 | 0.8088 | 0.8459 | 0.7922 |
经过第二轮搜索,模型评分(CV_score)进一步提高,并且训练集评分略有下降、但测试集评分有所提升,也说明模型泛化能力也得到了提高。
接下来进一步查看本轮搜索的到的最有超参数组:
grid_RF_0.best_params_
# {'max_depth': 11,
# 'max_features': 2,
# 'max_leaf_nodes': None,
# 'max_samples': 0.4,
# 'min_samples_leaf': 2,
# 'min_samples_split': 7,
# 'n_estimators': 90}
据此可以设置下一轮搜索策略:
- max_depth本轮最优取值为11,在原定搜索空间上界,下次搜索可以进一步向上拓展搜索空间;
- max_features本轮最优取值为2,是原定搜索空间的下界,下次搜索可向下拓展搜索空间,也就是将1带入进行搜索。但需要注意的是,sqrt作为非数值型结果,仍然需要带入进行搜索,这轮被淘汰并不代表重新调整搜索空间后仍然被淘汰;
- max_leaf_nodes本轮最优取值仍然为None,说明在一个更大的范围内进行更激进的搜索并没有达到预想的效果,下一轮可以反其道而行之,设置一个上一轮没有搜索到的数值较小的空间(1-20),来进行更加精准的搜索;
- max_samples本轮最优取值仍然为0.4,基本可以确定最优取值就在0.4附近,下一轮可以进一步设置一个步长更小的区间进行搜索;
- min_samples_leaf本轮最优取值为2,恰好落在本轮搜索空间的中间,下一轮搜索时不用调整取值;
- min_samples_split本轮最优取值仍然为7,恰好落在本轮搜索空间的中间,下一轮搜索时不用调整取值;
- n_estimators本轮最优取值为90,下一轮可以以90为中心,设置更小的范围进行搜索,但需要注意的是,上一轮n_estimators取值搜索的跨度为10,下轮搜索时可以缩减到4。
3.第三轮搜索
根据调整策略,开始第三轮搜索:
start = time.time()
# 设置超参数空间
parameter_space = {
"min_samples_leaf": range(1, 4),
"min_samples_split": range(6, 9),
"max_depth": range(10, 15),
"max_leaf_nodes": [None] + list(range(1, 20, 2)),
"n_estimators": range(85, 100, 4),
"max_features":['sqrt'] + list(range(1, 4)),
"max_samples":[None, 0.38, 0.4, 0.42]}
# 实例化模型与评估器
RF_0 = RandomForestClassifier(random_state=12)
grid_RF_0 = GridSearchCV(RF_0, parameter_space, n_jobs=15)
# 模型训练
grid_RF_0.fit(X_train_OE, y_train)
print(time.time()-start)
#1268.0402607917786
3.1 计算运行时间与参数空间
由于经过了两轮搜索,执行第三轮时预判即将能够搜网得到最优取值(实际并没有),因此设置了一个相比之前更大的超参数搜索空间:
3 * 3 * 4 * 11 * 4 * 4 * 4
#25344
在参数设置时,只在max_leaf_nodes参数部分增加设置了4个备选搜索取值,但参数空间就扩大成了第二轮搜索的参数空间的5倍,而本轮搜索耗时也差不多是第二轮计算用时的5倍:
1268.0402607917786/60
#21.134004346529643
1268.0402607917786 / 25344
#0.05003315422947359
约0.05s完成一组超参数搜索。
3.2 查看运行结果
接下来查看模型运行结果:
grid_RF_0.best_score_
#0.8087841518305094
grid_RF_0.score(X_train_OE, y_train), grid_RF_0.score(X_test_OE, y_test)
#(0.8415372964786065, 0.7927314026121521)
| Models | CV.best_score_ | train_score | test_score |
|---|---|---|---|
| Logistic+grid | 0.8045 | 0.8055 | 0.7932 |
| RF+grid_R1 | 0.8084 | 0.8517 | 0.7848 |
| RF+grid_R2 | 0.808785 | 0.8459 | 0.7922 |
| RF+grid_R3 | 0.808784 | 0.8415 | 0.7927 |
能够发现,第三轮搜索的结果相比第二轮,模型整体效果其实是略微下降的(根据CV.best_score_),这其实也是在超参数搜索过程是中经常会遇到的问题,也就是多轮搜索过程中模型评分可能出现波动的问题。不过不要气馁,继续观察本轮输出的最优超参数组,继续调参。
grid_RF_0.best_params_
# {'max_depth': 10,
# 'max_features': 'sqrt',
# 'max_leaf_nodes': None,
# 'max_samples': 0.38,
# 'min_samples_leaf': 3,
# 'min_samples_split': 7,
# 'n_estimators': 97}
- max_depth本轮最优取值为10,在原定搜索空间下界,下次搜索可以进一步向下拓展搜索空间,当然,根据第二轮第三轮max_depth在9和10反复变动的现象,估计max_depth最终的最优取值也就是9、10左右;
- max_features本轮最优取值又回到了sqrt,也就是4附近,结合第一轮sqrt的最优结果,预计max_features最终最优取值也就在4附近,接下来的搜索将是收尾阶段,我们可以设计一个sqrt+log2+4附近的搜索组合;
- max_leaf_nodes本轮最优取值仍然为None,三轮搜索都没有改变max_leaf_nodes的最优取值,并且本轮还设置了非常多的备选取值,说明max_leaf_nodes的最优取值极有可能就是None,接下来我们只需保留None+大范围搜索的组合即可,以防其他参数变动时max_leaf_nodes的最优取值发生变化;
- max_samples本轮最优取值变成了0.38,而训练集总样本数为5282,5282*0.38约为2007,下轮开始我们将把比例转化为具体的样本数,进行更加精准的搜索,及围绕2007附近的数值空间进行搜索;
- min_samples_leaf本轮最优取值为3,恰好落在本轮搜索空间的上届,下一轮搜索时略微拓展搜索空间的上界;
- min_samples_split本轮最优取值仍然为7,恰好落在本轮搜索空间的中间,下一轮搜索时不用调整取值;
- n_estimators本轮最优取值为97,下一轮可以以97为中心,设置更小的范围进行搜索;
X_train_OE.shape[0]
#5282
X_train_OE.shape[0] * 0.38
#2007.16
4.第四轮搜索
继续进行第四轮搜索:
start = time.time()
# 设置超参数空间
parameter_space = {
"min_samples_leaf": range(2, 5),
"min_samples_split": range(6, 9),
"max_depth": range(8, 12),
"max_leaf_nodes": [None] + list(range(10, 70, 20)),
"n_estimators": range(95, 105, 2),
"max_features":['sqrt', 'log2'] + list(range(1, 6, 2)),
"max_samples":[None] + list(range(2002, 2011, 2))}
# 实例化模型与评估器
RF_0 = RandomForestClassifier(random_state=12)
grid_RF_0 = GridSearchCV(RF_0, parameter_space, n_jobs=15)
# 模型训练
grid_RF_0.fit(X_train_OE, y_train)
print(time.time()-start)
#1218.2634932994843
4.1 计算运行时间与参数空间
由于很多参数都基本能确定最优值的范围,因此本轮搜索时很多参数都略微放大的参数取值范围,这也导致备选超参数组的数量急剧增加:
3 * 3 * 4 * 5 * 4 * 5 * 6
#21600
最终计算时长和第三轮搜索时的计算时长接近。
1218.2634932994843 / 60
#20.304391554991405
1218.2634932994843 / 21600
#0.0564010876527539
约0.06s执行完一组超参数搜索。
4.2 查看运行结果
接下来查看模型运行结果:
第相比第三轮搜索,第四轮的搜索结果有显著提高:
grid_RF_0.best_score_
#0.8095422651300135
grid_RF_0.score(X_train_OE, y_train), grid_RF_0.score(X_test_OE, y_test)
#(0.8405906853464596, 0.7881885292447472)
| Models | CV.best_score_ | train_score | test_score |
|---|---|---|---|
| Logistic+grid | 0.8045 | 0.8055 | 0.7932 |
| RF+grid_R1 | 0.8084 | 0.8517 | 0.7848 |
| RF+grid_R2 | 0.808785 | 0.8459 | 0.7922 |
| RF+grid_R3 | 0.808784 | 0.8415 | 0.7927 |
| RF+grid_R4 | 0.809542 | 0.8406 | 0.7882 |
接下来我们查看本轮输出的最优参数组,并制定后续搜索策略:
grid_RF_0.best_params_
#{'max_depth': 9,
# 'max_features': 5,
# 'max_leaf_nodes': None,
# 'max_samples': 2002,
# 'min_samples_leaf': 3,
# 'min_samples_split': 8,
# 'n_estimators': 99}
- max_depth本轮最优取值为9,能够进一步肯定max_depth最终的最优取值也就是9、10左右;
- max_features本轮最优取值变成了5,仍然在4附近变化,后续继续保留sqrt+log2+4附近的搜索组合;
- max_leaf_nodes本轮最优取值仍然为None,并没有发生任何变化,后续仍然保留原定搜索范围;
- max_samples本轮最优取值为2002,这是第一次围绕max_samples进行整数搜索,接下来可以以2002为中心,设置一个更小搜索空间;
- min_samples_leaf本轮最优取值为3,恰好落在本轮搜索空间的上届,下一轮搜索时略微拓展搜索空间的上界;
- min_samples_split本轮最优取值变成了8,根据之前的搜索结果,该参数最优取值基本都在7和8之间变动,因此可以设置一个6-9的搜索空间,确保下次如果再出现参数在7、8之间变动时,仍然在搜索范围内;
- n_estimators本轮最优取值为99,结合之前搜索出来的97的结果,预计该参数最终的最优取值应该就是97-99之间,可以据此设置下一轮搜索空间;
5.第五轮搜索
接下来,继续进行第五轮搜索。经过了前几轮搜索,大多数参数都已经能确定最优解的大概取值范围,因此第五轮搜索时可以将我们判断的可能的最优解全部包括在内,进行大规模搜索,当然,为了不至于搜索时间过长,我们可以适当删除部分我们判断不会出现最优解的取值范围:
start = time.time()
# "min_samples_leaf":以3为中心
# "min_samples_split":重点搜索7、8两个值
# "max_depth":重点搜索9、10两个值
# "max_leaf_nodes":大概率为None
# "n_estimators": 重点搜索97、98、99三个值
# "max_features":5附近的值+['sqrt', 'log2']
# "max_samples":2002向下搜索,重点搜索2002、2001和2000三个值
# 设置超参数空间
parameter_space = {
"min_samples_leaf": range(2, 5),
"min_samples_split": range(6, 10),
"max_depth": range(8, 12),
"max_leaf_nodes": [None],
"n_estimators": range(96, 101),
"max_features":['sqrt', 'log2'] + list(range(3, 7)),
"max_samples":[None] + list(range(2000, 2005))}
# 实例化模型与评估器
RF_0 = RandomForestClassifier(random_state=12)
grid_RF_0 = GridSearchCV(RF_0, parameter_space, n_jobs=15)
# 模型训练
grid_RF_0.fit(X_train_OE, y_train)
print(time.time()-start)
#604.7498576641083
5.1 计算运行时间与参数空间
这一轮中我们删除了max_leaf_nodes参数的数值取值,极大程度缩减了参数空间:
3 * 4 * 4 * 1 * 5 * 6 * 6
#8640
604.7498576641083 / 8640
#0.06999419648890141
因此最终计算用时控制在10分钟左右,平均0.07s执行一组超参数的计算。
5.2 查看运行结果
接下来查看模型运行结果,相比第四轮搜索,第五轮的搜索结果继续提升:
grid_RF_0.best_score_
#0.8104878013818411
grid_RF_0.score(X_train_OE, y_train), grid_RF_0.score(X_test_OE, y_test)
#(0.8483528966300644, 0.7955706984667802)
| Models | CV.best_score_ | train_score | test_score |
|---|---|---|---|
| Logistic+grid | 0.8045 | 0.8055 | 0.7932 |
| RF+grid_R1 | 0.8084 | 0.8517 | 0.7848 |
| RF+grid_R2 | 0.808785 | 0.8459 | 0.7922 |
| RF+grid_R3 | 0.808784 | 0.8415 | 0.7927 |
| RF+grid_R4 | 0.809542 | 0.8406 | 0.7882 |
| RF+grid_R5 | 0.810488 | 0.8483 | 0.7955 |
该结果也是目前的最好结果。
接下来继续查看超参数搜索结果:
grid_RF_0.best_params_
# {'max_depth': 10,
# 'max_features': 'sqrt',
# 'max_leaf_nodes': None,
# 'max_samples': 2000,
# 'min_samples_leaf': 2,
# 'min_samples_split': 7,
# 'n_estimators': 97}
能够看出,除了min_samples_leaf和max_samples各自取到了搜索范围下界外,其他参数的最优取值都在设置的取值范围中间。据此我们可以判断搜索任务即将结束,下一轮搜索极有可能是最后一轮搜索,为此我们可以制定下一轮搜索策略:除了刚才的两个参数需要调整取值范围外,其他参数可以以本次搜索结果为中心设置更大的取值范围,最好能包括最近三轮各参数的最优值点,同时max_leaf_nodes恢复之前的大范围数值搜索范围,这么做必然会导致参数空间变得非常大,但为了确保最终结果具有较高的可信度,最后一轮搜索建议放大范围,具体原因稍后解释。这里我们可以简单回顾最近三轮搜索时各参数的最优值点:
| leaf | split | depth | nodes | estimators | features | samples |
|---|---|---|---|---|---|---|
| 3 | 7 | 10 | None | 97 | sqrt | 0.38 |
| 3 | 8 | 9 | None | 99 | 5 | 2002 |
| 2 | 7 | 10 | None | 97 | sqrt | 2000 |
据此,我们可以设置最后一轮搜索超参数空间如下:
parameter_space = {
"min_samples_leaf": range(1, 5),
"min_samples_split": range(6, 10),
"max_depth": range(8, 12),
"max_leaf_nodes": [None] + list(range(10, 70, 20)),
"n_estimators": range(96, 101),
"max_features":['sqrt', 'log2'] + list(range(1, 7)),
"max_samples":[None] + list(range(1999, 2004))}
如此一来,最后一轮搜索的参数空间备选参数组数量如下:
4 * 4 * 4 * 4 * 5 * 8 * 6
#61440
而根据此前测算的平均计算时间,约0.06s完成一组超参数的计算,因此在总共有61440组超参数的情况下,最终估计计算时间为:
61440 * 0.06
#3686.3999999999996
61440 * 0.06 / 60
#61.43999999999999
约一小时。
6.第六轮搜索
接下来执行第六轮搜索:
start = time.time()
# 设置超参数空间
parameter_space = {
"min_samples_leaf": range(1, 5),
"min_samples_split": range(6, 10),
"max_depth": range(8, 12),
"max_leaf_nodes": [None] + list(range(10, 70, 20)),
"n_estimators": range(96, 101),
"max_features":['sqrt', 'log2'] + list(range(1, 7)),
"max_samples":[None] + list(range(1999, 2004))}
# 实例化模型与评估器
RF_0 = RandomForestClassifier(random_state=12)
grid_RF_0 = GridSearchCV(RF_0, parameter_space, n_jobs=15)
# 模型训练
grid_RF_0.fit(X_train_OE, y_train)
print(time.time()-start)
#3601.6263830661774
最终计算时间和此前预估相差不大,差不多1小时完成计算。
- 查看运行结果
接下来查看模型运行结果,能够发现,在修改了超参数搜索空间后,最终仍然输出了第五次搜索最终输出的结果。尽管没有模型效果上的提升,但两次重复的结果也让我们更加肯定当前输出的超参数组就是最优超参数组。
grid_RF_0.best_score_
#0.8104878013818411
grid_RF_0.score(X_train_OE, y_train), grid_RF_0.score(X_test_OE, y_test)
#(0.8483528966300644, 0.7955706984667802)
grid_RF_0.best_params_
# {'max_depth': 10,
# 'max_features': 'sqrt',
# 'max_leaf_nodes': None,
# 'max_samples': 2000,
# 'min_samples_leaf': 2,
# 'min_samples_split': 7,
# 'n_estimators': 97}
| Models | CV.best_score_ | train_score | test_score |
|---|---|---|---|
| Logistic+grid | 0.8045 | 0.8055 | 0.7932 |
| RF+grid_R1 | 0.8084 | 0.8517 | 0.7848 |
| RF+grid_R2 | 0.808785 | 0.8459 | 0.7922 |
| RF+grid_R3 | 0.808784 | 0.8415 | 0.7927 |
| RF+grid_R4 | 0.809542 | 0.8406 | 0.7882 |
| RF+grid_R5 | 0.810488 | 0.8483 | 0.7955 |
| RF+grid_final | 0.810488 | 0.8483 | 0.7955 |
最终,在当前建模流程和当前数据集情况下,随机森林能够达到的最好表现就是0.810488。
7.最优超参数组的可信度
通过结果我们不难发现,第六轮搜索的结果和第五轮搜索的结果并没有任何区别,那为何还要进行第六轮搜索?或者说,考虑到第五轮搜索时确实存在部分超参数取到了搜索区间的边界值,那简单拓展搜索边界即可,为何需要加入那么多备选参数、导致计算量激增?
这里就要介绍关于最优超参数组的可信度的问题了。其实从原理上来说,超参数和模型效果之间并没有真正意义上的凸函数关系,如果有这种关系,超参数就不是超参数、而是一般参数了,就可以采用其他更加自动化的优化算法来确定最优值了。因此,哪怕在第五轮的时候我们几乎可以确定超参数的最优取值,但在第六轮搜索时仍然需要扩大参数范围进行验证,就是担心万一超参数取值边界扩大、最优取值发生变化了呢?毕竟我们不能完全相信所谓凸函数的特征。
事实证明,这种担心也是必要的,我们可以查看如下一组结果:
grid_RF_0.best_score_
#0.8101093718643387
start = time.time()
# 设置超参数空间
parameter_space = {
"min_samples_leaf": range(1, 4),
"min_samples_split": range(6, 8),
"max_depth": range(9, 12),
"max_leaf_nodes": [None] + list(range(10, 70, 20)),
"n_estimators": range(98, 101),
"max_features":['sqrt', 'log2'] + list(range(1, 7)),
"max_samples":[None] + list(range(1999, 2002))}
# 实例化模型与评估器
RF_0 = RandomForestClassifier(random_state=12)
grid_RF_0 = GridSearchCV(RF_0, parameter_space, n_jobs=15)
# 模型训练
grid_RF_0.fit(X_train_OE, y_train)
print(time.time()-start)
#409.4373540878296
grid_RF_0.best_params_
#{'max_depth': 10,
# 'max_features': 'sqrt',
# 'max_leaf_nodes': None,
# 'max_samples': 2000,
# 'min_samples_leaf': 2,
# 'min_samples_split': 7,
# 'n_estimators': 99}
grid_RF_0.score(X_train_OE, y_train), grid_RF_0.score(X_test_OE, y_test)
#(0.8492995077622113, 0.7938671209540034)
能够看到,在这次搜索中,确实每个超参数最终取值都落在搜索区间的中间,也似乎满足了我们之前介绍的搜索停止的条件。但是最终输出结果并不如我们上面第六轮搜索得到的结果。对比最终输出的超参数也能看出,其实差距就在n_estimators的取值,n_estimators在[98,99,100]中搜索时,最优取值是99,但如果稍微放宽搜索区间时,如设置为[96, 97, 98, 99, 100],也就是第六轮搜索时的参数设置,此时网格搜索会判断n_estimators的最优取值为97。这也说明至少n_estimators的取值和模型效果并不是“凸函数”的关系(因为如果是,则模型效果会在n_estimators=97左右两边单调变化,在搜索[98,99,100]时将判断98是最优取值)。但同时,97这个取值也并不陌生,在相对精准的第三轮搜索时就被选为最优超参数取值,因此,为了一定抵消超参数和模型效果之间这种不确定性关系所带来的风险,最后一轮搜索时必须扩大搜索范围,最好是将前几轮精确搜索(不是大步长搜索)得出的结果一起带入进行搜索,以期得到一个相对更加准确的结论。
不过尽管如此,我们也不能百分之百确定目前第六轮搜索出来的结果就一定是绝对意义的最优解、就不存在比这组超参数更优的解,但我们仍然建议采用上述流程进行搜索,也是因为这是长期实践经验总结的产物,根据长期实践证明,这样的一套搜索策略能够以非常高的效率得到一个相对来说非常好的结果(大概率是全域最优解),尽管不是100%的最优解,但这其实是我们借助有限的算力去解决无限的未知的一种手段,毕竟超参数空间取值理论上是无限的,枚举不可能穷尽,目前也没有理论可以通过某种公式确定最优解(贝叶斯也只是估计)。
- 借助有限的资源去解决无限的未知,这就是“人”的价值
当然,既然讨论到关于“借助有限的算力去解决无限的未知”的问题,我们也可以从这个角度出发,简单探讨关于AutoML的发展方向与当前算法工程师的可能存在的职业发展焦虑的问题。从根本上来说,机器学习模型的超参数看起来是模型的“缺陷”,因为如果没有超参数的话,模型就可以完全自动化训练了,模型确定参数就像 y = x 2 y=x^2 y=x2找最小值一样简单,但实际上,机器学习模型的超参数确是解决模型“缺陷”的手段。简单理解,世界上并不存在绝对意义上完美的机器学习模型,影响模型的所有变量并不能够通过一套理论完美求解,因此机器学习模型选择将将所有的不确定性都交给了超参数,才使得参数能够顺利的被求解,这样也才使得其基本原理得以成立。而正式因为这些超参数的优化需要人去解决,算法工程师的工作才变得有价值和有意义——能够帮助模型达到更好的效果(“《自私的模型》”),当然,特征工程也是类似。但是,如果某一天人们创造了某个算法没有超参数、或者超参数求解的问题能够被一套理论或者一套计算流程完美解决,这个过程不需要人工干预,那么算法工程师的工作价值可能就会大打折扣。不过值得庆幸的是,截止目前,并没有这种算法或者相关理论出现,甚至这都不是一个热门的研究方向,因为大多数学者判断,以当前基础科学发展情况来看(主要是基础数学和物理),这些理论突破暂时不可能做到。
而新兴的AutoML,听名字好像是全自动化机器学习,但其实并不是完全自动化解决超参数优化的问题,而是将超参数优化问题转化为了另一种更高层次的建模问题,但这个问题仍然需要人来解决,也就是需要算法工程人员去解决,只不过不再是一个个参数进行调节,而是使用一个更加复杂的工具来进行模型整体层面的优化,你可以将AutoML看成是一个更加高级的网格搜索工具,效果更好、理论更加复杂、操作难度更高。不过截至目前,尽管AutoML得到了一定程度的应用,但其基础理论和实践工具仍然有待进一步的突破,才能够成为新的算法工程师们趁手的工具。
所以说替代算法工程师工作的不是某个工具,而是一个没有“超参数”的世界,或者说,当模型不再需要“人”去优化时。
8.其他搜索方案
当然,除了网格搜索外,此处也可以考虑先进行大规模随机网格搜索或者对半搜索,锁定的最优参数后再划定范围进行更加精准的网格搜索,也就是所谓的组合搜索策略,不过由于初始搜索出来的最优参数精度不够,外加随机搜索时抽样过程不确定,也会对最终结果造成影响。其实从另一个角度来看,网格搜索前几轮设置的大步长搜索策略,其实也就相当于是随机网格搜索,只不过随机抽样的取值是人工固定的。
三、网格搜索流程总结
最后,让我们简单总结上述介绍的网格搜索实战流程,帮助大家从一个更加整体的角度看待网格搜索参数优化的全过程。
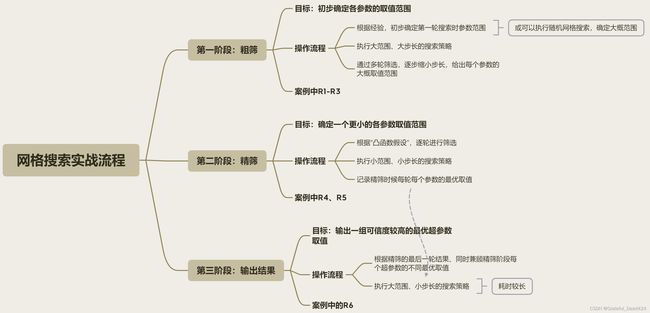 至此,我们就完成了随机森林+网格搜索在当前数据集上的全部训练与优化工作,并借此完整详细的介绍了网格搜索这一优化器的具体实战操作技巧。当然,要做到活学活用,还需要在日后更多的实践中不断积累经验,需要注意的是,后续课程中在进行网格搜索调优时,只会展示最后一轮的搜索结果,但实际搜索流程和本节介绍的一致,也希望同学课后多加练习,甚至提炼和总结自己的调优流程。
至此,我们就完成了随机森林+网格搜索在当前数据集上的全部训练与优化工作,并借此完整详细的介绍了网格搜索这一优化器的具体实战操作技巧。当然,要做到活学活用,还需要在日后更多的实践中不断积累经验,需要注意的是,后续课程中在进行网格搜索调优时,只会展示最后一轮的搜索结果,但实际搜索流程和本节介绍的一致,也希望同学课后多加练习,甚至提炼和总结自己的调优流程。