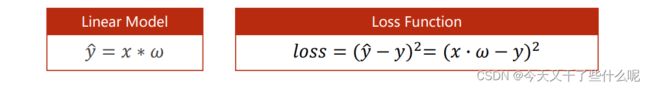【PyTorch深度学习实践】深度学习之反向传播，用PyTorch实现线性回归和Logistic回归

---

前言

继上一节讲的线性模型和梯度下降法后，本节将在此基础上讲解反向传播，用PyTorch实现线性回归和Logistics回归

---

一、反向传播

误差反向传播法（Back-propagation,BP）会计算神经网络中损失函数对各参数的梯度，配合优化方法更新参数，降低损失函数。
BP本来只指损失函数对参数的梯度通过网络反向流动的过程，但现在也常被理解成神经网络整个的训练方法，由误差传播、参数更新两个环节循环迭代组成。

依旧是选择上一篇文章讲的线性模型来讲解反向传播法，如上图所示，从左向右看，在构建线性模型y=wx并且求损失函数的过程中，我们可以得到中间这些变量对x和w的导数。而经过反向传播后，也就是从右向左看，反向传播法是能够自动求出损失函数对各参数的梯度的。那么对于上一节讲的线性模型，我们的目的是为了找到一个合适的权重w，所用的方法是损失函数对权重w求梯度，这不正好与咱们这一节所要讲的反向传播相对应了吗

反向传播的过程比较简单，以这个线性模型为例，先定义好线性模型和损失函数，在计算完损失值后进行反向传播(backward)，并更新权重w即可，代码如下：

import torch

x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]

w=torch.Tensor([1.0])
w.requires_grad=True

def forward(x):
    return w*x

def loss(x,y):
    y_pred=forward(x)
    return (y_pred-y)**2

print("predict(before training)",4,forward(4).item())

for epoch in range(100):
    for x,y in zip(x_data,y_data):
        l=loss(x,y)              #计算损失值
        l.backward()             #反向传播
        print('\tgrad',x,y,w.grad.item())
        w.data=w.data-0.01*w.grad.data      #更新权重w

        w.grad.data.zero_()              #将第一轮反向传播后的权重w清零，不能影响下一轮反向传播的权重w

    print("progress:",epoch,l.item())

print("predict(after training)",4,forward(4).item())

大概训练20次左右，损失值便很小了

二、用PyTorch实现线性回归

用PyTorch实现线性回归，就是用PyTorch里面的模块来实现我们之前讲述的线性模型。PyTorch的模式比较一致，大致有四步构成：
1.准备数据集
2.设计模型
3.构建损失函数和优化器
4.训练（前馈，反向传播，更新参数）
如下图所示：

代码如下：

import torch

#准备数据集
x_data=torch.Tensor([[1.0],[2.0],[3.0]])   #3行1列的矩阵
y_data=torch.Tensor([[2.0],[4.0],[6.0]])

#设计模型
class LinearModel(torch.nn.Module):       #定义线性模型，继承自Module
    def __init__(self):
        super(LinearModel,self).__init__()   #初始化，调用父类的构造
        self.linear=torch.nn.Linear(1,1)     #线性函数Linear,包含两个参数，权重w和偏置b

    def forward(self,x):
        y_pred=self.linear(x)         #设计线性模型
        return y_pred

model=LinearModel()

#构造损失函数和优化器
criterion=torch.nn.MSELoss(size_average=False)    #损失函数MSE
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)    #优化器，随机梯度下降SGD

#训练
for epoch in range(1000):           #训练1000次,100次效果不太好
    y_pred=model(x_data)
    loss=criterion(y_pred,y_data)
    print(epoch,loss.item())

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

print('w=',model.linear.weight.item())
print('b=',model.linear.bias.item())

x_test=torch.Tensor([[4.0]])
y_test=model(x_test)
print('y_pred=',y_test.data)

三、Logistic回归

Logistic回归与线性回归不同，它解决的是一个分类问题，它的输出结果是离散的，输出的是各个分类对象的概率

例如：识别手写数字集，这是一个分类问题，共分成0~9十个分类，用逻辑回归做输出结果是离散的，通过概率来识别数字

下面的动物识别也是一个分类问题，同上面的类似

在二分类问题中，只有0和1两类，输出结果是0或者1出现的概率

既然要表示概率，概率的取值是0~1的，那我们应该选择一个取值在0到1的函数来处理输出值，sigmoid函数就非常适合完成这项工作
—————————————————————————————————

sigmoid函数：

由函数图像可知，sigmoid函数有几个很好的性质：

• 当z趋近于正无穷大时，σ(z) = 1
• 当z趋近于负无穷大时，σ(z) = 0
• 当z = 0时，σ(z) = 0.5

将经过线性变化的值放入sigmoid函数中处理，这样结果就在0~1之间了

与线性回归的MSE损失函数不同的是，二分类问题的损失函数如下图所示，y代表分类是0还是1的概率。

总的来说，逻辑回归与线性回归主要有两处不同：
一：逻辑回归的中间值经过了sigmoid函数的处理
二：两种模型的损失函数不同
逻辑回归的代码如下：

import torch
import torch.nn.functional as F

#准备数据集
x_data=torch.Tensor([[1.0],[2.0],[3.0]])
y_data=torch.Tensor([[0],[0],[1]])

#设计模型
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel,self).__init__()
        self.liner=torch.nn.Linear(1,1)

    def forward(self,x):
        y_pred=F.sigmoid(self.liner(x))    #线性函数经过sigmoid函数处理
        return y_pred

model=LogisticRegressionModel()

#构造损失函数和优化器
criterion=torch.nn.BCELoss(size_average=False)      #逻辑回归的损失函数BCE
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)

#训练
for epoch in range(1000):
    y_pred=model(x_data)
    loss=criterion(y_pred,y_data)      #计算损失值
    print(epoch,loss.item())

    optimizer.zero_grad()           #优化器清零
    loss.backward()                 #反向传播
    optimizer.step()                #更新

import numpy as np
import matplotlib.pyplot as plt

x=np.linspace(0,10,200)
x_t=torch.Tensor(x).view((200,1))
y_t=model(x_t)
y=y_t.data.numpy()
plt.plot(x,y)
plt.plot([0,10],[0.5,0.5],c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()

总结

本文主要讲述了反向传播的作用，以及用PyTorch实现线性回归和逻辑回归的过程，比较了这两种模型的不同之处。最后大家需要重点牢记的就是那四个步骤，准备数据集，设计模型，构建损失函数和优化器，训练（前馈，反向传播，更新参数）。