【吴恩达深度学习】：第二周编程作业（笔记型）——01

参考资料来源

本文主要内容是参照该博主编写的，以下是原文链接：https://blog.csdn.net/u013733326/article/details/79639509

一、简介

吴恩达深度学习第二周作业，第二周主要讲述的是逻辑回归学习算法，我们主要做的是搭建一个能够"识别猫"的简单神经网络。

二、编程前的准备工作

2.1 知识点

2.1.1 向量维度和数据维度

向量维度：x ： 一维向量
（x1，x2）： 二维向量
（x1,x2,x3） : 三维向量
（x1,x2…,xn） : n维向量

数据维度：

2.1.2 符号定义

x : 表示一个nx维数据，为输入数据，维度为（nx，1）
y : 表示输出结果，取值为（0，1）
(((),()) : 表示第i组数据，可能是训练数据，也可能是测试数据，此处默认为训练数据
=[(1),(2),…,()]：表示所有的训练数据集的输入值，放在一个 ×的矩阵中，
其中 表示样本数目 ;
=[(1),(2),…,()]：对应表示所有训练数据集的输出值，维度为 1×。
X ：为了能把训练集表示的更紧凑，定义一个矩阵用大写的X表示，矩阵X会由训练样本按照行堆叠起来而不是列
注：上述小括号（）都表示上标；

2.2 函数

2.2.1 逻辑回归的Hypothesis Function（假设函数）

sigmoid函数：（在这里z是一个实数，如果z非常大那么e^(-z)将会接近于0）

2.2.2 逻辑回归的Loss Function（损失函数）

（用来衡量算法的运行情况）

损失函数用来衡量输出值和实际值有多接近，一般情况下我们用预测值和实际值的平方差或者他们平方差的一半，但是通常在逻辑回归中我们不这么做。

2.2.3 逻辑回归的Logistic Regression Cost Function（代价函数）

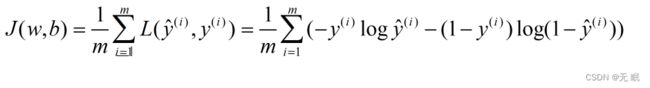
损失函数只是用于单个训练样本，而代价函数是参数的总代价，所以在训练逻辑回归模型的时候，我们需要找到合适的w和b，来让代价函数J的总代价降到最低。

2.3 梯度下降法

梯度下降法能用来做什么？
在你的测试集上，通过最小化代价函数（成本函数）J（w,b）来训练参数w和b

：= 表示更新参数
α 表示学习率，用来控制步长
dJ(w)/dw 表示向下走一步的长度，就是J(w)对w求导
dJ(w)/dw > 0 : 斜率为负，向左走一步
dJ(w)/dw < 0 : 斜率为正，向右走一步

两个参数：

2.4 向量化

（向量化是非常基础的去除代码中for循环的艺术）

举个简单的例子：如果你使用for循环
z=0
for i in range(n_x)
z+=w[i]*x[i]
z+=b
而向量化的代码是：
z=np.dot(w,x)+b

向量化节约时间，可以快速的得到结果，在深度学习中记住要避免使用显示for循环

向量化方式就是 u = np.dot(A,v):
np.dot()函数主要有两个功能，向量点积和矩阵乘法,这里需要注意的是一维矩阵和一维向量的区别，一维向量的shape是(5, ), 而一维矩阵的shape是(5, 1), 若两个参数a和b都是一维向量则是计算的点积，但是当其中有一个是矩阵时（包括一维矩阵），dot便进行矩阵乘法运算。所以如果是一个向量和一个矩阵相乘，这个向量会自动转换为一维矩阵进行计算。

2.5 python广播

x = np.random.rand(3,3) #返回一个或一组服从”0~1“均匀分布的随机样本函数值。取值范围[0,1）
y = x.sum(axis=0) #表示求和顺序按列执行
z = x.sum(axis=1) #表示求和顺序按行执行
print("随即创建的3x3矩阵为：")
print(x)
print("按列求和后的结果为：")
print(y)
# print(z)
percentage = 100*x/y.reshape(1,3)
print("每一列中单个元素占比：")
print(percentage)

看上述函数，运行结果如下：

随即创建的3x3矩阵为：
[[0.52780426 0.23421259 0.78153587]
 [0.3425774  0.04111998 0.84307445]
 [0.8982751  0.67628568 0.71993669]]
按列求和后的结果为：
[1.76865677 0.95161825 2.34454701]
每一列中单个元素占比：
[[29.84209661 24.61203253 33.33419489]
 [19.36935481  4.32105797 35.95894842]
 [50.78854859 71.0669095  30.70685668]]

Process finished with exit code 0

axis用来指明将要进行的运算是沿着哪个轴执行，在 numpy中， 0轴是垂直的，也就是列，而 1轴是水平的，也就是行。

上述代码中的x.reshape(1,3)指令就是调用了numpy中的广播机制，当我们写代码的时不确定矩阵的维度，通常会对矩阵进行重塑操作，重塑操作reshape是一个常量的时间的操作，时间复杂度是O(1),调用代价极低。（广播机制与执行的运算种类无关）

如果两个数组的后缘维度的轴长度相符或其中一方的轴长度为1，则认为它们是广播兼容的。广播会在缺失维度和轴长度为 1的维度上进行。

后缘维度的轴长度：A.shape[ 1] 即矩阵维度元组中的最后一个位置的值

注：如果我们不完全确定一个向量的维度(dimension)，我们会经常扔进一个断言语句（assertion statement）

三、编程

见下篇