《图机器学习》-Traditional Methods for Machine Learning in Graphs
Traditional Methods for Machine Learning in Graphs
- 前言
- 一、Node-Level Tasks and Features
- 二、Link-Level Tasks and Features
- 三、Graph-Level Tasks and Features
前言
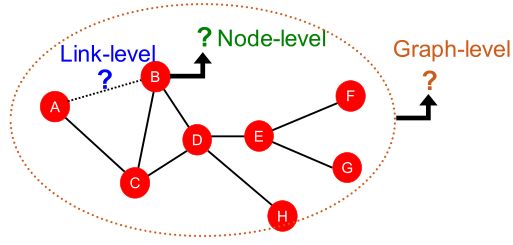
图机器学习任务可以分为三种:
- Node-level prediction:节点级的预测
- 如对节点进行类别预测
- Link-level prediction:边级的预测
- 如预测两节点之间以多大的概率存在一条边
- Graph-level prediction:图级的预测
- 如预测某个分子是否含有某种属性
传统的机器学习会去设计节点、边、图的特征向量,然后获取一组有标签的训练集数据,在这组训练集上去训练机器学习模型(如 R a n d o m f o r e s t Random\ forest Random forest、 S V M SVM SVM、 N e u r a l n e t w o r k Neural\ network Neural network)。
对于新的节点、边、图,将其特征向量作为机器学习模型的输入与并得到预测。
【即主要做的是学习一个函数 f f f, f f f能够有效的将输入的特征向量 x x x映射到输出 y y y】
所以,使用传统算法,在图上使用有效的特征是获得良好模型性能的关键。
本章节主要探讨在节点、边、图上如何设计合适的特征向量。为了方便,仅关注无向图。
一、Node-Level Tasks and Features
先举一个半监督学习的例子:
绿色、红色分别代表不同类型的节点,灰色节点代表待分类的节点。如下图;
现想将灰色的节点进行分类,我们将度数大于等于2的节点归类为绿色节点,度数为1的节点归类为红色节点。

所以我们需要找到一个来能表示节点属性的feature来进行分类;上述例子中的feature是节点的度。
所以我们的目标是:
找到能够描述节点在网络中结构与位置的特征
可行的特征有:
- N o d e d e g r e e Node\ degree Node degree
- N o d e c e n t r a l i t y Node\ centrality Node centrality
- C l u s t e r i n g c o e f f i c i e n t Clustering\ \ coefficient Clustering coefficient
- G r a p h l e t s Graphlets Graphlets
N o d e d e g r e e Node\ degree Node degree:
节点度 k v k_v kv表示的是节点 v v v相邻节点的个数。如下图;
如 C C C节点和 E E E节点的度数 k k k都为3,所以通过 N o d e d e g r e e Node\ degree Node degree会判定这两个节点具有相同的属性特征。
然而两个节点在空间上的位置不同,邻居节点也不同,可能会具有不同的重要性或者属性特征。但是通过 N o d e d e g r e e Node\ degree Node degree并不能表示出这一不同。
N o d e c e n t r a l i t y Node\ centrality Node centrality:
N o d e c e n t r a l i t y Node\ centrality Node centrality特征考虑了图中节点的重要性,我们用 c v c_v cv来表示 v v v节点的 N o d e c e n t r a l i t y Node\ centrality Node centrality特征值。
下面主要介绍三种不同可以衡量节点的重要性的 N o d e c e n t r a l i t y Node\ centrality Node centrality:
- E n g i e n v e c t o r c e n t r a l i t y Engienvector\ centrality Engienvector centrality
- B e t w e e n n e s s c e n t r a l i t y Betweenness\ centrality Betweenness centrality
- C l o s e n e s s c e n t r a l i t y Closeness\ centrality Closeness centrality
E n g i e n v e c t o r c e n t r a l i t y Engienvector\ centrality Engienvector centrality:
思想:
如果节点 v v v被重要的相邻节点包围,则节点 v v v是重要的。
因此节点 v v v的 c v c_v cv为其相邻节点 c e n t r a l i t y centrality centrality的和,计算公式如下:
c v = 1 λ ∑ u ∈ N ( v ) c u c_v=\frac{1}{λ}\sum \limits _{u∈N(v)}c_u cv=λ1u∈N(v)∑cu
- λ λ λ是一个用于标准化的常数,其值一般为邻接矩阵的最大特征值
将上诉式子向量化:
c v = 1 λ ∑ u ∈ N ( v ) c u ⟺ λ c = A c c_v=\frac{1}{λ}\sum \limits _{u∈N(v)}c_u \iff λc=Ac cv=λ1u∈N(v)∑cu⟺λc=Ac
- A A A:邻接矩阵; A u v = 1 i f u ∈ N ( v ) A_{uv}=1\ if\ u∈N(v) Auv=1 if u∈N(v)
- c c c: C e n t r a l i t y v e c t o r Centrality\ vector Centrality vector
- λ λ λ: A A A的特征值,通常将 A A A的最大特征值 λ m a x λ_{max} λmax对应的特征向量 c m a x c_{max} cmax当作 c e n t r a l i t y centrality centrality
B e t w e e n n e s s c e n t r a l i t y Betweenness\ centrality Betweenness centrality:
思想:
如果一个节点位于其他节点之间的许多最短路径上,那么它就很重要。
其公式如下:
c v = ∑ s ≠ v ≠ t 从节点 s 到节点 t 中途经过节点 v 的最短路径数量 从节点 s 到节点 t 最短路径数量 c_v=\sum \limits _{s≠v≠t}\frac{从节点s到节点t中途经过节点v的最短路径数量}{从节点s到节点t最短路径数量} cv=s=v=t∑从节点s到节点t最短路径数量从节点s到节点t中途经过节点v的最短路径数量
实例:
C l o s e n e s s c e n t r a l i t y Closeness\ centrality Closeness centrality:
思想:
如果一个节点到所有其他节点的最短路径长度很小,那么这个节点就很重要。
其公式如下:
c v = 1 ∑ v ≠ u 从 u 到 v 最短路径长度 c_v=\frac{1}{\sum _{v≠u}从u到v最短路径长度} cv=∑v=u从u到v最短路径长度1
即 c v c_v cv值为从 v v v到其他节点最短路径之和的倒数。
C l u s t e r i n g c o e f f i c i e n t Clustering\ coefficient Clustering coefficient:
C l u s t e r i n g c o e f f i c i e n t Clustering\ coefficient Clustering coefficient通过测量邻居节点的连接情况来描述节点的特征,公式如下:
e v = 节点 v 邻居节点之间的边数 C k v 2 ∈ [ 0 , 1 ] e_v=\frac{节点v邻居节点之间的边数}{C^2_{k_v}}∈[0,1] ev=Ckv2节点v邻居节点之间的边数∈[0,1]
- e k e_k ek:节点 v v v的 C l u s t e r i n g c o e f f i c i e n t Clustering\ coefficient Clustering coefficient
- k v k_v kv:节点 v v v的度
- C n m C^m_{n} Cnm:组合数
C k v 2 C^2_{k_v} Ckv2表示邻居节点之间有可能构成多少条边,上式的分子表示实际上邻居节点之间存在多少条边,所以 e v e_v ev可以看作是衡量节点邻居的连接有多紧密的度量。
例子:
第一幅图: e v = 6 C 4 2 = 6 6 = 1 e_v=\frac{6}{C_4^2}=\frac{6}{6}=1 ev=C426=66=1
第二幅图: e v = 3 C 4 2 = 3 6 = 0.5 e_v=\frac{3}{C_4^2}=\frac{3}{6}=0.5 ev=C423=63=0.5
第三幅图: e v = 0 C 4 2 = 0 6 = 0 e_v=\frac{0}{C_4^2}=\frac{0}{6}=0 ev=C420=60=0
一个观察:
我们可以以顶点 v v v为根,通过计算图片中三角形的数量来评估其重要性。如下图:
在社交网络中,会存在很多这种三角形,因为你的两个朋友可能会以你为媒介相互认识,从而构成一个三元组,形成一个三角形。
将上述观察进行扩展,将寻找三角形替换成:寻找某些预定义的子图 p r e − s p e c i f i e d s u b g r a p h pre-specified\ subgraph pre−specified subgraph,这就是下面将要介绍的 g r a p h l e t s graphlets graphlets。
G r a p h l e t s Graphlets Graphlets:
G r a p h l e t s Graphlets Graphlets中文翻译为:根连通诱导非同构子图。

如上图:给出了至多5个节点的73个不同的 g r a p h l e t s graphlets graphlets。
什么是 g r a p h l e t s graphlets graphlets?
给定节点个数 k k k, k k k个节点构成的异构(化学上的异构)图为可称为 g r a p h l e t s graphlets graphlets
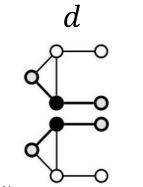
以3个节点为例,规定了3个节点,3个节点可以构造出两个异构图 G 1 、 G 2 G_1、G_2 G1、G2, G 1 、 G 2 G_1、G_2 G1、G2就是两个 g r a p h l e t s graphlets graphlets。
图中标数字的节点表示为可以当做根的节点,如 G 1 G_1 G1,该图以中间节点对称,所以头结点和尾结点是等价的,所以可以作为根的只有其中一个端结点和中间结点。再如 G 2 G_2 G2,三个顶点都是等价的,所以只能选择其中一个作为根。
G r a p h l e t D e g r e e V e c t o r ( G D V ) : Graphlet Degree Vector (GDV): GraphletDegreeVector(GDV):
基于给定根节点的 g r a p h l e t s graphlets graphlets的计数向量
我们要计算图 G G G关于 u u u的 G D V GDV GDV,即给定了根节点 u u u。
这里 g r a p h l e t s graphlets graphlets是结点至多为3的异构图集合:

首先考虑第一个 g r a p h l e t graphlet graphlet,然后在图 G G G寻找:将 a a a放到 u u u的位置,寻找可以以 g r a p h l e t graphlet graphlet结构构成诱导子图的个数;这里可构成的个数是2;如下图:

再考虑第二个 g r a p h l e t graphlet graphlet,如下图:

再考虑第三个 g r a p h l e t graphlet graphlet,
-
首先考虑以 c c c为根的 g r a p h l e t graphlet graphlet
数量是 0 0 0, G G G中存在第三个 g r a p h l e t graphlet graphlet的结构,但是构不成 g r a p h l e t graphlet graphlet的诱导子图。因为 G G G中的相比 g r a p h l e t graphlet graphlet多了一条边(下图的红色)边。
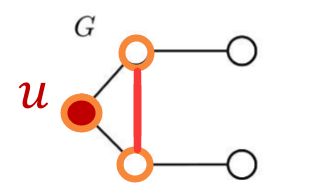
所以结点 u u u的 G D V = [ 2 , 1 , 0 , 2 ] GDV=[2,1,0,2] GDV=[2,1,0,2]
二、Link-Level Tasks and Features
l i n k l e v e l P r e d i c t i o n link\ level\ Prediction link level Prediction的任务是根据现有链路预测新的链路。在测试模型的时候,对图中不存在的链接预测其存在的概率后对其进行排序,将排在前 K K K个最可能存在的链接作为预测结果返回。
该任务的关键是为一对顶点设计合适的特征。
因为预测的链路都是不存在的,所以只能够通过顶点的来抽象的描述这条不存在链路的特征。
l i n k p r e d i c t i o n link\ prediction link prediction任务解决的两种方案:
- L i n k s m i s s i n g a t r a n d o m Links\ missing\ at\ random Links missing at random(随机丢失链接):
该方法主要用于静态图中,随机的去除图中的一些边,然后训练一个模型以最大化的概率去预测这些去掉的边。 - L i n k s o v e r t i m e Links\ over\ time Links over time(随时间变化的链接):
该方法主要用于动态图中,给定一个 t 0 t_0 t0到 t 0 ′ t^{'}_0 t0′时刻的图 G [ t 0 , t 0 ′ ] G[t_0,t^{'}_0] G[t0,t0′],然后训练一个模型能够输出一个按照链接出现概率为排名的列表 L L L,该列表 L L L中的链接是在 G [ t 0 , t 0 ′ ] G[t_0,t^{'}_0] G[t0,t0′]不存在的链接,但在下一时刻的图 G [ t 1 , t 1 ′ ] G[t_1,t^{'}_1] G[t1,t1′]中出现的链接。
链接预测步骤:
- 描述链接存在可能性,需要对每对顶点 ( x , y ) (x,y) (x,y),计算出一个分数 c ( x , y ) c(x,y) c(x,y),当作其存在的概率的评估。
- 按照分数 c ( x , y ) c(x,y) c(x,y)对每对顶点 ( x , y ) (x,y) (x,y)进行排序
- 取前 n n n个顶点对作为链接预测的返回结果
- 评判预测结果
关于顶点对的分数,可以以下三种方式给出:
- D i s t a n c e − b a s e d f e a t u r e Distance-based\ feature Distance−based feature
- L o c a l n e i g h b o r h o o d o v e r l a p Local\ neighborhood\ overlap Local neighborhood overlap
- G l o b a l n e i g h b o r h o o d o v e r l a p Global\ neighborhood\ overlap Global neighborhood overlap
该分数可以当作链路的 f e a t u r e feature feature用于链路预测。
D i s t a n c e − b a s e d f e a t u r e Distance-based\ feature Distance−based feature:
思想:
两个节点之间的最短路径距离作为该顶点对的得分/feature。
该方法的缺点在于没有考虑顶点对邻居的重合度。
如顶点对 ( B , H ) (B,H) (B,H)之间有共同的两个邻居,顶点对 ( B , E ) (B,E) (B,E)之间只有一个共同的邻居,然而这两个顶点对的得分都是 2 2 2;即 d i s t a n c e − b a s e d f e a t u r e distance-based\ feature distance−based feature并不能够表示出该信息。
L o c a l n e i g h b o r h o o d o v e r l a p Local\ neighborhood\ overlap Local neighborhood overlap:
为了能够表示出顶点对邻居的重合度,提出了 l o c a l n e i g h b o r h o o d o v e r l a p local\ neighborhood\ overlap local neighborhood overlap。
方式一: C o m m o n n e i g h b o r s Common\ neighbors Common neighbors
将共同的邻居作为其得分,公式为:
∣ N ( v 1 ) ∩ N ( v 2 ) ∣ |N(v_1)∩N(v_2)| ∣N(v1)∩N(v2)∣
实例:
对于下图,顶点对 ( A , B ) (A,B) (A,B)的得分为1,因为 A A A和 B B B只存在一个共同的邻居 C C C,即 ∣ N ( A ) ∩ N ( B ) ∣ = ∣ { C } ∣ = 1 |N(A)∩N(B)|=|\{C\}|=1 ∣N(A)∩N(B)∣=∣{C}∣=1

该方式的问题在于:度高的顶点对就会有更高的结果。所以提出了一种类似于归一化的方式 J a c c a r d ’ s c o e f f i c i e n t Jaccard’s\ coefficient Jaccard’s coefficient。
方式二: J a c c a r d ’ s c o e f f i c i e n t Jaccard’s\ coefficient Jaccard’s coefficient
其顶点对得分公式为:
∣ N ( v 1 ) ∩ N ( v 2 ) ∣ ∣ N ( v 1 ) ∪ N ( v 2 ) ∣ \frac{|N(v_1)∩N(v_2)|}{|N(v_1)∪N(v_2)|} ∣N(v1)∪N(v2)∣∣N(v1)∩N(v2)∣
实例:
对于下图,顶点对 ( A , B ) (A,B) (A,B)的得分为2,因为 A A A和 B B B只存在一个共同的邻居 C C C,即 ∣ N ( A ) ∩ N ( B ) ∣ ∣ N ( A ) ∪ N ( B ) ∣ = ∣ { C } ∣ { ∣ C , D ∣ } = 2 \frac{|N(A)∩N(B)|}{|N(A)∪N(B)|}=\frac{|\{C\}|}{\{|C,D|\}}=2 ∣N(A)∪N(B)∣∣N(A)∩N(B)∣={∣C,D∣}∣{C}∣=2

方式三: A d a m i c − A d a r i n d e x Adamic-Adar\ index Adamic−Adar index
其顶点对得分公式为:
∑ u ∈ N ( v 1 ) ∩ N ( v 2 ) 1 l o g ( k u ) \sum _{u∈N(v_1)∩N(v_2)} \frac{1}{log(k_u)} u∈N(v1)∩N(v2)∑log(ku)1
即对顶点对的共同邻居的度取对数;
该方法当共同的邻居结点的度较少时,会获得更高的得分。 A d a m i c − A d a r i n d e x Adamic-Adar\ index Adamic−Adar index在实践中表现得比较好,尤其在社交网络上,因为我们希望有一堆度数低的共同好友比有一堆名人共同好友的得分更高。
G l o b a l n e i g h b o r h o o d o v e r l a p Global\ neighborhood\ overlap Global neighborhood overlap:
l o c a l n e i g h b o r h o o d f e a t u r e s local\ neighborhood\ features local neighborhood features存在得缺点:
当两个结点之间没有共同邻居,则该顶点对的得分很可能为0。但这两个顶点还是有可能被链接起来的。
如下图:
所以进一步提出了 g l o b a l n e i g h b o r h o o d o v e r l a p global\ neighborhood\ overlap global neighborhood overlap,该方法通过通过考虑整个图来解决这个限制。
K a t z i n d e x Katz\ index Katz index:
思想:
计算给定节点对之间所有长度的路径的总和,将其当作得分。
得分可表示为:
s u , v = ∑ l = 1 ∞ ( u 到 v 长度为 l 的路径的条数 ) s_{u,v}=\sum_{l=1}^{∞}(u到v长度为l的路径的条数) su,v=l=1∑∞(u到v长度为l的路径的条数)
那么如何计算长度为 l l l的路径有多少条呢?
还记得邻接矩阵的定义: A u , v = 1 i f u ∈ N ( v ) A_{u,v}=1\ if\ u∈N(v) Au,v=1 if u∈N(v)
将 P ( K ) u v P^(K)_{uv} P(K)uv定义为从 u u u到 v v v长度为 K K K的路径条数。
可以观察到: P ( 1 ) = A P^{(1)}=A P(1)=A,因为 A A A表示的就是结点之间能否一跳到达。
如何计算 P u v ( 2 ) P^{(2)}_{uv} Puv(2)呢?
- 步骤一:首先计算从 u u u到 v v v之间长度为 1 1 1的路径的条数,这个可以直接根据邻接矩阵得出,我们表示为 P u v ( 1 ) P^{(1)}_{uv} Puv(1)。
- 步骤二:对于长度为 2 2 2的路径,可以看作:
- 已知 P u v ( 1 ) P^{(1)}_{uv} Puv(1)
- 考虑 u u u通过第 i i i个结点再到 v v v,以这样的方式将路径长度加一
- 然后判断是否存在这一条路径,在将其结果相加即可,如下定义:
P u v ( 2 ) = ∑ i A u i ∗ P i v ( 1 ) = ∑ i A u i ∗ A i v = A u v 2 P^{(2)}_{uv}= \sum _iA_{ui}*P^{(1)}_{iv}=\sum _iA_{ui}*A_{iv}=A^2_{uv} Puv(2)=i∑Aui∗Piv(1)=i∑Aui∗Aiv=Auv2
∑ i A u i ∗ P i v ( 1 ) \sum _iA_{ui}*P^{(1)}_{iv} ∑iAui∗Piv(1):
- P i v ( 1 ) = x P^{(1)}_{iv}=x Piv(1)=x则表示 i i i到 v v v有 x x x条长度为 1 1 1的路径
- A u i = 1 A_{ui}=1 Aui=1表示存在 u u u到 i i i的路径;反之不存在。
- A u i ∗ P i v ( 1 ) A_{ui}*P^{(1)}_{iv} Aui∗Piv(1)表示:我 u u u先通过 i i i,再经过 i i i到 v v v这条长度为 1 1 1的路径存不存在。若不存在则数值为0,存在其值就是路径的个数。
可以通过数学归纳法去证明,当执行到第 i i i步:
- 已知 P u v ( i − 1 ) P^{(i-1)}_{uv} Puv(i−1),求 P u v ( i ) P^{(i)}_{uv} Puv(i)
- P u v ( i ) P^{(i)}_{uv} Puv(i)定义如下:
P u v ( i ) = ∑ i A u i ∗ P i v ( i − 1 ) = ∑ i A u i ∗ A i v i − 1 = A u v i P^{(i)}_{uv}= \sum _iA_{ui}*P^{(i-1)}_{iv}=\sum _iA_{ui}*A^{i-1}_{iv}=A^i_{uv} Puv(i)=i∑Aui∗Piv(i−1)=i∑Aui∗Aivi−1=Auvi
所以最后得到结论:
P ( k ) = A K \color{red}{P^{(k)}=A^{K}} P(k)=AK
所以 K a t z i n d e x Katz\ index Katz index的定义更新如下:
S u , v = ∑ l = 1 ∞ β l A u , v l S_{u,v}=\sum\limits^{∞}_{l=1}\ β^l\ A^l_{u,v} Su,v=l=1∑∞ βl Au,vl
- β β β: d i s c o u n t f a c t o r discount\ factor discount factor( 0 < β < 1 0 <β< 1 0<β<1),其作用时希望路径长度越长的路径权重越小,即对得分的贡献越小。
上面的定义可以进一步推导成:
S u , v = ∑ l = 1 ∞ β l A u , v l = ( I − β A ) − 1 − I S_{u,v}=\sum\limits^{∞}_{l=1}\ β^l\ A^l_{u,v}=(I-βA)^{-1}-I Su,v=l=1∑∞ βl Au,vl=(I−βA)−1−I
推导过程:
S = β A + β 2 A 2 + ⋯ + β ∞ A ∞ S=βA+β^2A^2+\cdots+β^∞A^∞ S=βA+β2A2+⋯+β∞A∞
.
( I − β A ) ( I + S ) (I-βA)(I+S) (I−βA)(I+S)
= ( I − β A ) ( I + β A + β 2 A 2 + ⋯ ) =(I-βA)(I+βA+β^2A^2+\cdots) =(I−βA)(I+βA+β2A2+⋯)
= ( I + β A + β 2 A 2 + ⋯ ) − ( β A + β 2 A 2 + β 3 A 3 + ⋯ ) =(I+βA+β^2A^2+\cdots)-(βA+β^2A^2+β^3A^3+\cdots) =(I+βA+β2A2+⋯)−(βA+β2A2+β3A3+⋯)
= I =I =I
.
因此, S u , v = ( I − β A ) − 1 − I S_{u,v}=(I-βA)^{-1}-I Su,v=(I−βA)−1−I
三、Graph-Level Tasks and Features
Graph-Level Features的目标是:
想要得到一个描述整个图结构的features。
K e r n e l M e t h o d s Kernel\ Methods Kernel Methods:
在传统的ML中, k e r n e l m e t h o d s kernel\ methods kernel methods被广泛用于图级预测。
该方法的中心思想是:
设计一个核函数来用于图级任务的完成,而不是设计特征向量。
K e r n e l s Kernels Kernels的简单介绍:
- k e r n e l kernel kernel K ( G , G ′ ) ∈ R K(G,G^{'})∈R K(G,G′)∈R,其值表示图 G G G和 G ′ G^{'} G′的相似度
- 存在图级的特征表示 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅)使得: K ( G , G ′ ) = ϕ ( G ) T ϕ ( G ′ ) K(G,G^{'})=\phi(G)^T\phi(G^{'}) K(G,G′)=ϕ(G)Tϕ(G′)
- ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅)可以不被显示的给出,所以定义了核函数就可以用于机器学习模型(如 k e r n e l S V M kernel\ SVM kernel SVM)
G r a p h K e r n e l s Graph\ Kernels Graph Kernels:用于衡量两张图之间的相似程度。具体的核函数方法有以下两种:
- G r a p h l e t K e r n e l Graphlet\ Kernel Graphlet Kernel
- W e i s f e i l e r − L e h m a n K e r n e l Weisfeiler-Lehman\ Kernel Weisfeiler−Lehman Kernel
当然还有其他核函数,本文不做介绍:
- Random-walk kernel
- Shortest-path graph kernel
- And many more…
G r a p h K e r n e l Graph\ Kernel Graph Kernel的思路:
- 先设计图级的特征向量 ϕ ( G ) \phi(G) ϕ(G)。
- 在通过 ϕ ( G ) T ϕ ( G ′ ) \phi(G)^T\phi(G^{'}) ϕ(G)Tϕ(G′)得到核函数值
关键思想: Bag-of-Words (BoW) for a graph
首先了解什么是Bag-of-Words:
在文本任务中,会简单的使用单词的数量作为该文本的特征向量。
如下面的句子:
S = “ I a m S a m , I a m b a t m a n " S=“I\ am\ Sam,I\ am\ batman" S=“I am Sam,I am batman"
我们可以用下面的向量标识该文本:
ϕ ( S ) = I a m S a m b a t m a n [ 2 2 1 1 ] \phi(S)=\begin{matrix} \ \ \ \ \ \ \ I \ \ \ \ \ am \ \ \ \ Sam \ \ batman \\ \begin{bmatrix} 2 && 2& &1&&1 \\ \end{bmatrix} \\ \end{matrix} ϕ(S)= I am Sam batman[2211]
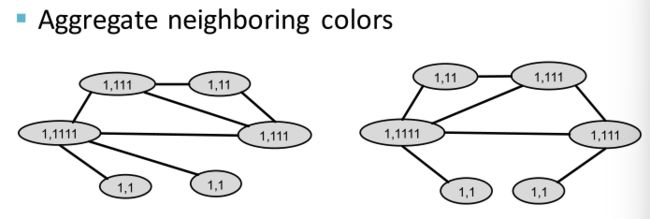
可以将图的结点当作单词,然后使用 B O W BOW BOW;如下图,由于两个图都有4个节点,所以得到了两个不同图的相同特征向量。

我们也可以将图结点的度作为单词,使用 B O W BOW BOW;如下图:

Graphlet Kernel和Weisfeiler−Lehman Kernel都运用了 B a g − o f − ∗ \color{red}{Bag-of-*} Bag−of−∗的思想表示一张图, ∗ * ∗是一个比结点度、结点数量更复杂的度量。
G r a p h l e t K e r n e l Graphlet\ Kernel Graphlet Kernel:
思路:
计算图中不同的 g r a p h l e t s graph lets graphlets的数量。
注意:
图级的 g r a p h l e t s graphlets graphlets和结点级的 g r a p h l e t s graph lets graphlets在定义上有些不同:
- 图级的graphlet中的 g r a p h l e t graphlet graphlet可以是不连通的,而结点级的 g r a p h l e t graphlet graphlet必须是连通的。
- 图级的 g r a p h l e t graphlet graphlet不需要指定根节点。
例子:
当图的节点个数为3时,有4个 g r a p h l e t graphlet graphlet;如下图:

当图的节点个数为4时,有11个 g r a p h l e t graphlet graphlet;如下图:

给定图 G G G,使用 g k = ( g 1 , g 2 , ⋯ , g n k ) g_k=(g_1,g_2,\cdots,g_{nk}) gk=(g1,g2,⋯,gnk)表示节点至多为 k k k的 g r a p h l e t graphlet graphlet列表。
并定义 G G G的 g r a p h l e t c o u n t v e c t o r graphlet\ count\ vector graphlet count vector为 f G ∈ R n k f_G∈R^{n_k} fG∈Rnk,定义如下:
( f G ) i = G 中存在 g i 的诱导子图的个数 (f_G)_i=G中存在g_i的诱导子图的个数 (fG)i=G中存在gi的诱导子图的个数
以 k = 3 k=3 k=3为例,如下图:

给定两个图 G 、 G ′ G、G^{'} G、G′, g r a p h l e t k e r n e l graphlet\ kernel graphlet kernel的计算公式如下:
K ( G , G ′ ) = f G T f G ′ K(G,G^{'})=f_G^Tf_{G^{'}} K(G,G′)=fGTfG′
当 G G G和 G ′ G^{'} G′的节点数量相差很大时, f G f_G fG和 f G ′ f_{G^{'}} fG′里面的值的数量级也会相差很大,所以在 g r a p h l e t k e r n e l graphlet\ kernel graphlet kernel的计算前先对其使用归一化:
h G = f G S u m ( f G ) , K ( G , G ′ ) = h G T h G ′ h_G=\frac{f_G}{Sum(f_G)},K(G,G^{'})=h_G^Th_{G^{'}} hG=Sum(fG)fG,K(G,G′)=hGThG′
g r a p h l e t k e r n e l graphlet\ kernel graphlet kernel的缺点:
g r a p h l e t graphlet graphlet的计数是很昂贵的:
- 对于一个大小为n的图,通过枚举计算大小为k的graphlets需要nk
- 子图同构检验是一个 N P − h a r d NP-hard NP−hard问题
下面介绍一个更加高效的 g r a p h k e r n e l graph\ kernel graph kernel:Weisfeiler−Lehman Kernel
W e i s f e i l e r − L e h m a n K e r n e l Weisfeiler−Lehman\ Kernel Weisfeiler−Lehman Kernel:
该方法的目标是:
设计一个更加高效的图特征描述向量 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅)
思想:
使用邻域结构迭代丰富节点信息。
实现算法: C o l o r r e f i n e m e n t Color\ refinement Color refinement
- 给定一个图 G G G和一个顶点集 V V V
- 为每个节点 v v v都设置为一个随机的颜色 c ( 0 ) ( v ) c^(0)(v) c(0)(v)
- 通过下式迭代的更新节点的颜色:
c ( v ) ( k + 1 ) = H A S H ( { c ( k ) ( v ) , c ( k ) ( u ) u ∈ N ( v ) } ) c^{(k+1)}_{(v)}=HASH(\{c^{(k)}(v),c^{(k)}(u)_{u∈N(v)}\}) c(v)(k+1)=HASH({c(k)(v),c(k)(u)u∈N(v)})- H A S H ( ) HASH() HASH()表示为一个哈希函数
- 通过上一轮迭代的顶点颜色和其邻居的颜色作为hash函数的输入,通过hash函数将不同的输入映射为不同的颜色
- 经过 K K K步色彩迭代, c ( v ) ( K ) c^{(K)}_{(v)} c(v)(K)可以获取 K − h o p K-hop K−hop(K跳)邻域的节点结构信息
例子:
W L k e r n e l WL\ kernel WL kernel在计算更有效率:
- 每一步颜色汇聚更新的时间复杂度是线性的,因为它只涉及到聚集相邻的颜色。
- 在计算内核值时,只需要跟踪两个图中出现的颜色。因此,向量中最大的元素值只能是节点的个数。
- 计数颜色仅需要线性时间 O ( n k ) O(n_k) O(nk)。
- 总的来说,时间复杂度是线性的