NLP经典论文:ELMo 笔记
NLP经典论文:ELMo 笔记
- 论文
- 介绍
- 模型结构
- 文章部分翻译
-
- Abstract
- ELMo: Embeddings from Language Models
-
- 3.1 Bidirectional language models
- 3.2 ELMo
- 3.3 Using biLMs for supervised NLP tasks
- 3.4 Pre-trained bidirectional language model architecture
- 相关视频
- 相关的笔记
- 相关代码
-
- pytorch
- tensorflow
-
- keras
- pytorch API:
- tensorflow API
论文
NLP论文笔记合集(持续更新)
原论文:《Deep contextualized word representations》
介绍
2018/01/01发表的文章,传统的word embedding无法解决一词多义,也不含有上下文信息,是没有语境的词语表示。该文章提出了深层语境化的词语表示法,即词语的表示能够含有上下文信息,是处于一定语境下的词语表示,以此作为下游任务(如情感分析等)的输入,来代替传统的word embedding。ELMo 使用多个 BiLSTM 层,将输入在不同层中进行表示,然后将这些表示进行 weighted sum,可用于下游任务作为额外的输入表示。
同时它的名字也和美国育儿卡通节目《芝麻街》里面的一个角色一样。

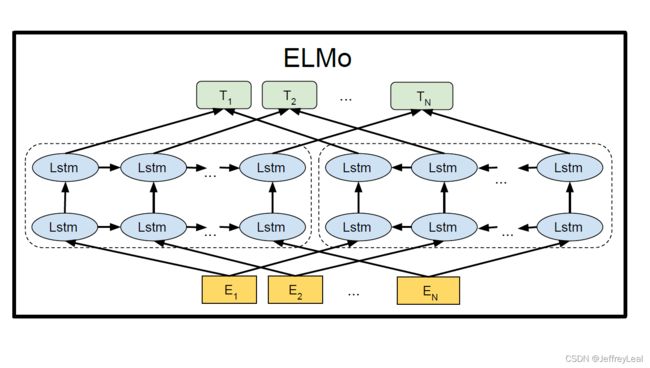
模型结构
给定 n n n 个 token 序列 ( w 1 , w 2 , … , w n ) (w_1,w_2,…,w_n) (w1,w2,…,wn)
前向LSTM网络给定输入: ( ′ B O S ′ , w 1 , … , w n − 1 , w n ) ('BOS',w_1,…,w_{n-1},w_n) (′BOS′,w1,…,wn−1,wn),期望输出是: ( w 1 , w 2 , … , w n , ′ E O S ′ ) (w_1,w_2,…,w_n,'EOS') (w1,w2,…,wn,′EOS′)
后向LSTM网络给定输入: ( ′ E O S ′ , w n , … , w 2 , w 1 ) ('EOS',w_n,…,w_2,w_1) (′EOS′,wn,…,w2,w1),期望输出是: ( w n , w n − 1 , … , w 1 , ′ B O S ′ ) (w_n,w_{n-1},…,w_1,'BOS') (wn,wn−1,…,w1,′BOS′)
以下第一个结构为 L L L 层前向LSTM网络,第二个结构为 L L L 层后向LSTM网络。
[ 前 向 L S T M 预 测 词 w 1 w 2 ⋯ w k + 1 ⋯ w n ′ E O S ′ s o f t m a x 层 ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ 输 出 e m b e d d i n g 层 W o h → 0 , L W o h → 1 , L ⋯ W o h → k , L ⋯ W o h → n − 1 , L W o h → n , L 第 L 层 h → 0 , L h → 1 , L ⋯ h → k , L ⋯ h → n − 1 , L h → n , L ⋮ ⋮ ⋮ ⋱ ⋮ ⋱ ⋮ ⋮ 第 1 层 h → 0 , 1 h → 1 , 1 ⋯ h → k , 1 ⋯ h → n − 1 , 1 h → n , 1 输 入 e m b e d d i n g 层 h 0 , 0 h 1 , 0 ⋯ h k , 0 ⋯ h n − 1 , 0 h n , 0 前 向 L S T M 输 入 层 ′ B O S ′ w 1 ⋯ w k ⋯ w n − 1 w n 输 入 时 刻 0 1 ⋯ k ⋯ n − 1 n ] \begin{bmatrix} 前向LSTM预测词&w_1&w_2&\cdots&w_{k+1}&\cdots&w_n&'EOS'\\ softmax层&{\cdots}&{\cdots}&{\cdots}&{\cdots}&{\cdots}&{\cdots}&{\cdots}\\ 输出embedding层&W_o\overrightarrow{h}_{0,L}&W_o\overrightarrow{h}_{1,L}&{\cdots}&W_o\overrightarrow{h}_{k,L}&{\cdots}&W_o\overrightarrow{h}_{n-1,L}&W_o\overrightarrow{h}_{n,L}\\ 第L层&\overrightarrow{h}_{0,L}&\overrightarrow{h}_{1,L}&{\cdots}&\overrightarrow{h}_{k,L}&{\cdots}&\overrightarrow{h}_{n-1,L}&\overrightarrow{h}_{n,L}\\ {\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}&{\ddots}&{\vdots}&{\vdots}\\ 第1层&\overrightarrow{h}_{0,1}&\overrightarrow{h}_{1,1}&{\cdots}&\overrightarrow{h}_{k,1}&{\cdots}&\overrightarrow{h}_{n-1,1}&\overrightarrow{h}_{n,1}\\ 输入embedding层&h_{0,0}&h_{1,0}&{\cdots}&h_{k,0}&{\cdots}&h_{n-1,0}&h_{n,0}\\ 前向LSTM输入层&'BOS'&w_1&{\cdots}&w_{k}&{\cdots}&w_{n-1}&w_{n}\\ 输入时刻&0&1&{\cdots}&k&{\cdots}&n-1&n\\ \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡前向LSTM预测词softmax层输出embedding层第L层⋮第1层输入embedding层前向LSTM输入层输入时刻w1⋯Woh0,Lh0,L⋮h0,1h0,0′BOS′0w2⋯Woh1,Lh1,L⋮h1,1h1,0w11⋯⋯⋯⋯⋱⋯⋯⋯⋯wk+1⋯Wohk,Lhk,L⋮hk,1hk,0wkk⋯⋯⋯⋯⋱⋯⋯⋯⋯wn⋯Wohn−1,Lhn−1,L⋮hn−1,1hn−1,0wn−1n−1′EOS′⋯Wohn,Lhn,L⋮hn,1hn,0wnn⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤ [ 后 向 L S T M 预 测 词 w n w n − 1 ⋯ w k − 1 ⋯ w 1 ′ B O S ′ s o f t m a x 层 ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ 输 出 e m b e d d i n g 层 W o h ← n + 1 , L W o h ← n , L ⋯ W o h ← k , L ⋯ W o h ← 2 , L W o h ← 1 , L 第 L 层 h ← n + 1 , L h ← n , L ⋯ h ← k , L ⋯ h ← 2 , L h ← 1 , L ⋮ ⋮ ⋮ ⋱ ⋮ ⋱ ⋮ ⋮ 第 1 层 h ← n + 1 , 1 h ← n , 1 ⋯ h ← k , 1 ⋯ h ← 2 , 1 h ← 1 , 1 输 入 e m b e d d i n g 层 h n + 1 , 0 h n , 0 ⋯ h k , 0 ⋯ h 2 , 0 h 1 , 0 后 向 L S T M 输 入 层 ′ E O S ′ w n ⋯ w k ⋯ w 2 w 1 输 入 时 刻 0 1 ⋯ k ⋯ n − 1 n ] \begin{bmatrix} 后向LSTM预测词&w_{n}&w_{n-1}&\cdots&w_{k-1}&\cdots&w_1&'BOS'\\ softmax层&{\cdots}&{\cdots}&{\cdots}&{\cdots}&{\cdots}&{\cdots}&{\cdots}\\ 输出embedding层&W_o\overleftarrow{h}_{n+1,L}&W_o\overleftarrow{h}_{n,L}&{\cdots}&W_o\overleftarrow{h}_{k,L}&{\cdots}&W_o\overleftarrow{h}_{2,L}&W_o\overleftarrow{h}_{1,L}\\ 第L层&\overleftarrow{h}_{n+1,L}&\overleftarrow{h}_{n,L}&{\cdots}&\overleftarrow{h}_{k,L}&{\cdots}&\overleftarrow{h}_{2,L}&\overleftarrow{h}_{1,L}\\ {\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}&{\ddots}&{\vdots}&{\vdots}\\ 第1层&\overleftarrow{h}_{n+1,1}&\overleftarrow{h}_{n,1}&{\cdots}&\overleftarrow{h}_{k,1}&{\cdots}&\overleftarrow{h}_{2,1}&\overleftarrow{h}_{1,1}\\ 输入embedding层&h_{n+1,0}&h_{n,0}&{\cdots}&h_{k,0}&{\cdots}&h_{2,0}&h_{1,0}\\ 后向LSTM输入层&'EOS'&w_n&{\cdots}&w_{k}&{\cdots}&w_{2}&w_{1}\\ 输入时刻&0&1&{\cdots}&k&{\cdots}&n-1&n\\ \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡后向LSTM预测词softmax层输出embedding层第L层⋮第1层输入embedding层后向LSTM输入层输入时刻wn⋯Wohn+1,Lhn+1,L⋮hn+1,1hn+1,0′EOS′0wn−1⋯Wohn,Lhn,L⋮hn,1hn,0wn1⋯⋯⋯⋯⋱⋯⋯⋯⋯wk−1⋯Wohk,Lhk,L⋮hk,1hk,0wkk⋯⋯⋯⋯⋱⋯⋯⋯⋯w1⋯Woh2,Lh2,L⋮h2,1h2,0w2n−1′BOS′⋯Woh1,Lh1,L⋮h1,1h1,0w1n⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤其中 h k , 0 h_{k,0} hk,0 是 输入embedding层中 t k t_k tk 的embedding, h k , 0 ∈ R d e m b × 1 h_{k,0}\in R^{d_{emb}\times 1} hk,0∈Rdemb×1。
h → k , j , h ← k , j \overrightarrow{h}_{k,j},\overleftarrow{h}_{k,j} hk,j,hk,j 分别代表前向和后向LSTM网络第 j j j 层第 k k k 个状态, j = 1 , . . . L j=1,...L j=1,...L, h → k , j , h ← k , j ∈ R d e m b / 2 × 1 \overrightarrow{h}_{k,j},\overleftarrow{h}_{k,j}\in R^{d_{emb}/2\times 1} hk,j,hk,j∈Rdemb/2×1。
令 h k , j = [ h → k , j ; h ← k , j ] h_{k,j}=[\overrightarrow{h}_{k,j};\overleftarrow{h}_{k,j}] hk,j=[hk,j;hk,j] ,用于特定下游任务的第 k k k 个输入的ELMO向量表示为: ELMo k t a s k = γ t a s k ∑ j = 0 L s j t a s k h k , j , k = 1 , . . . , n . \text{ELMo}_k^{task}=\gamma ^{task}\sum\limits _{j=0}^L s_j^{task} h_{k,j},\quad k=1,...,n. ELMoktask=γtaskj=0∑Lsjtaskhk,j,k=1,...,n.其中 s t a s k s^{task} stask 是待学习的softmax归一化权重,标量参数 γ t a s k \gamma ^{task} γtask 允许任务模型缩放整个ELMo向量以适应下游任务。
前向和后向LSTM的输入embedding空间 W i W_i Wi 是共享的, W i ∈ R d e m b × C W_i\in R^{d_{emb}\times C} Wi∈Rdemb×C, C C C为词汇表的大小;
前向和后向LSTM的输出embedding空间 W o W_o Wo,即softmax前的那个线性层,也是共享的, W o ∈ R C × d e m b W_o\in R^{C\times d_{emb}} Wo∈RC×demb。
假设下游任务的输入 token 为 x x x,将其输入到pre-trained的ELMo中得到ELMo x _x x,拼接后得到 [ x , ELMo x ] [x,\text{ELMo}_x] [x,ELMox]作为下游任务的新输入。
文章部分翻译
Abstract
我们介绍了一种新型的深层语境化的词语表示法,它对(1)词语使用的复杂特征(如语法和语义)和(2)如何使用这些在不同的语言语境中变化的特征(即,对多义词进行建模)进行建模。我们的词向量是深度双向语言模型(biLM)内部状态经学习后的功能表现形式,该模型是在大型文本语料库上预先训练的。我们表明,这些表示可以很容易地添加到现有的模型中,并在六个具有挑战性的NLP问题(包括问题回答、文本蕴涵和情感分析)中显著提高了目前的技术水平。我们的分析表明,显露预训练网络的深层内部是重要的,它允许下游模型混合不同类型的半监督信号。
ELMo: Embeddings from Language Models
与最广泛使用的word embedding不同(Pen nington et al.,2014),ELMo单词表示是整个输入句子的作用表现形式,如本节所述。它们通过字(character)卷积(第3.1节)在两层BiLM上计算,作为内部网络状态的线性函数(第3.2节)。这种设置允许我们进行半监督学习,其中biLM是大规模预训练的(第3.4节),并且很容易融入广泛的现有神经NLP架构(第3.3节)。
3.1 Bidirectional language models
给定 N N N 个 token 序列 ( t 1 , t 2 , … , t N ) (t_1,t_2,…,t_N) (t1,t2,…,tN),前向语言模型计算此序列的概率,通过建模给定的前文序列 ( t 1 , . . . , t k − 1 ) (t_1,...,t_{k-1}) (t1,...,tk−1) 来计算 token t k t_k tk 的概率: p ( t 1 , t 2 , . . . , t N ) = ∏ k = 1 N p ( t k ∣ t 1 , t 2 , . . . , t k − 1 ) . p(t_1, t_2, . . . , t_N )=\prod\limits_{k=1}^N p(t_k | t_1, t_2, . . . , t_{k−1}). p(t1,t2,...,tN)=k=1∏Np(tk∣t1,t2,...,tk−1).
最新最先进的神经语言模型(J o ˊ \acute{o} oˊzefowicz等人,2016年;Melis等人,2017年;Merity等人,2017年)计算上下文无关的 token 表示 x k L M x_k^{LM} xkLM(通过token embedding或字(character)级别上的CNN),然后将其传递给前向LSTM的层。在每一个位置 k k k,每一个LSTM层输出一个上下文无关的表示 h → k , j L M \overrightarrow{h}_{k,j}^{LM} hk,jLM,其中 j = 1 , . . . , L j=1,...,L j=1,...,L。最上层的LSTM输出 h → k , L L M \overrightarrow{h}_{k,L}^{LM} hk,LLM,通过一个sofomax层来预测下一个 token t k + 1 t_{k+1} tk+1。
除了后向LM是基于序列的逆序以外,它与前向LM是类似的,基于后文来预测前文的token: p ( t 1 , t 2 , . . . , t N ) = ∏ k = 1 N p ( t k ∣ t k + 1 , t k + 2 , . . . , t N ) . p(t_1, t_2, . . . , t_N )=\prod\limits_{k=1}^N p(t_k | t_{k+1}, t_{k+2}, . . . , t_N). p(t1,t2,...,tN)=k=1∏Np(tk∣tk+1,tk+2,...,tN).
它可以以类似于前向LM的方式实现,每个后向LSTM层 j j j 在 L L L 层深度模型中产生基于 ( t k + 1 , . . . , t N ) (t_{k+1}, . . . , t_N) (tk+1,...,tN) 的 t k t_k tk 表示 h → k , j L M \overrightarrow{h}_{k,j}^{LM} hk,jLM。
biLM结合了前向和后向LM。我们的公式联合最大化了向前和向后方向的对数似然: ∑ k = 1 N ( log p ( t k ∣ t 1 , . . . , t k − 1 ; Θ x , Θ → L S T M , Θ s ) + log p ( t k ∣ t k + 1 , . . . , t N ; Θ x , Θ ← L S T M , Θ s ) ) . \sum\limits_{k=1}^N(\log p(t_k | t_1, . . . , t_{k−1};\Theta_x,\overrightarrow{\Theta}_{LSTM},\Theta_s)+\log p(t_k | t_{k+1}, . . . , t_N;\Theta_x,\overleftarrow{\Theta}_{LSTM},\Theta_s)). k=1∑N(logp(tk∣t1,...,tk−1;Θx,ΘLSTM,Θs)+logp(tk∣tk+1,...,tN;Θx,ΘLSTM,Θs)).
我们将 token 表示( Θ x \Theta_x Θx)和Softmax层( Θ s \Theta_s Θs)的参数分别都在向前和向后网络之间共享,同时在每个方向上为LSTM保留单独的参数。总体而言,该公式与Peters等人(2017)的方法相似,但我们在方向之间共享一些权重,而不是使用完全独立的参数。在下一节中,我们将从以前的工作出发,介绍一种新的学习单词表示的方法,该方法是biLM层的线性组合。
(注:原文中的tie,是指前向和后向LSTM的输入embedding之间共享权重,前向和后向LSTM的输出embedding之间也共享权重)
3.2 ELMo
ELMo是biLM中应用于特定任务的中间层表示的组合。对于每个 token t k t_k tk,L层biLM计算一组2L+1表示 R k = { x k L M , h → k , j L M , h ← k , j L M ∣ j = 1 , . . . , L } = { h k , j L M ∣ j = 1 , . . . , L } R_k=\{x_k^{LM},\overrightarrow{h}_{k,j}^{LM},\overleftarrow{h}_{k,j}^{LM}|j=1,...,L\}=\{h_{k,j}^{LM}|j=1,...,L\} Rk={xkLM,hk,jLM,hk,jLM∣j=1,...,L}={hk,jLM∣j=1,...,L}其中 h k , 0 L M h_{k,0}^{LM} hk,0LM 是 token 层, h k , j L M = [ h → k , j M L ; h ← k , j L M ] h_{k,j}^{LM}=[\overrightarrow{h}_{k,j}^{ML};\overleftarrow{h}_{k,j}^{LM}] hk,jLM=[hk,jML;hk,jLM] 属于每一个biLSTM层。
为了能囊括在下游模型中,ELMo将 R R R 中的所有层折叠为一个向量, ELMo k = E ( R k ; Θ e ) \text{ELMo}_k=E(R_k;\Theta _e) ELMok=E(Rk;Θe)。在最简单的情况下,ELMo只选择顶层, E ( R k ) = h k , L L M E(R_k)=h_{k,L}^{LM} E(Rk)=hk,LLM,正如TagLM(Peters等人,2017年)和CoVe(Mc Cann等人,2017年)所述。更一般地说,我们计算所有biLM层的任务特定权重: ELMo k t a s k = E ( R k ; Θ t a s k ) = γ t a s k ∑ j = 0 L s j t a s k h k , j L M . ( 1 ) \text{ELMo}_k^{task}=E(R_k;\Theta ^{task})=\gamma ^{task}\sum\limits _{j=0}^L s_j^{task} h_{k,j}^{LM}.\quad (1) ELMoktask=E(Rk;Θtask)=γtaskj=0∑Lsjtaskhk,jLM.(1)
(注:感觉这里 h k , 0 L M h_{k,0}^{LM} hk,0LM 和 h k , j L M h_{k,j}^{LM} hk,jLM 能相加,意味着embedding维度是隐藏层维度的2倍。)
在(1)中, s t a s k s^{task} stask 是softmax归一化权重,标量参数 γ t a s k \gamma ^{task} γtask 允许任务模型缩放整个ELMo向量。 γ \gamma γ 对于辅助优化过程具有重要的实际意义(详见辅助材料)。考虑到每个biLM层的激活具有不同的分布,在某些情况下,它也有助于在 s t a s k s^{task} stask 加权前对每个biLM层应用layer normalization(Ba等人,2016)。
3.3 Using biLMs for supervised NLP tasks
给定一个预训练的biLM和有监督的应用于目标NLP任务的结构,使用biLM改进任务模型是一个简单的过程。我们只需运行biLM并记录每个单词在所有图层的表示。然后,我们让终端的任务模型学习这些表示的线性组合,如下所述。
首先考虑没有BiLM的监督模型的最低层。大多数受监督的NLP模型在最底层共享一个公共架构,使得我们可以以一致、统一的方式添加ELMo。给定一个 token 序列 ( t 1 , t 2 , … , t N ) (t_1,t_2,…,t_N) (t1,t2,…,tN),使用预先训练的 word embedding 和可选的基于字(character)的表示为每个 token 位置形成上下文无关的 token 表示 x k x_k xk 是标准的步骤。然后,该模型形成上下文相关的表示 h k h_k hk,通常使用双向RNN、CNN或前馈网络。
为了将ELMo添加到监督模型中,我们首先固定biLM的权重,然后将ELMo向量 ELMo t a s k _{task} task 与 x k x_k xk 拼接起来,并将ELMo增强表示 [ x k ; ELMo t a s k ] [x_k;\text{ELMo}_{task}] [xk;ELMotask] 传递到任务RNN中。对于某些任务(如SNLI、SQuAD),我们通过引入另一组专门用于输出的线性权重并将 h k h_k hk 替换为 [ h k ; ELMo t a s k ] [h_k;\text{ELMo}_{task}] [hk;ELMotask],从而在任务RNN的输出中加入ELMo,可观察到进一步的改进。由于监督模型的其余部分保持不变,这些添加可以在更复杂的神经模型中发生。例如,请参阅第4节中的SNLI实验,其中的BiLSTM层后面接着双向attention层,或参阅指代消解实验,其中的聚类模型位于BiLSTM之上。
(注:感觉这里任务RNN的第一层输入维度增长了,参数也应该增加,第二层开始参数就不用变化直到输出层,如果输出层有专门用于输出的线性权重,则参数也增加。)
最后,我们发现适当增加ELMo的 dropout 率是有益的(Srivastava等人,2014年),在某些情况下,通过增加损失 λ ∥ w ∥ 2 2 \lambda \|w\|_2^2 λ∥w∥22 来调整ELMo的权重。这对ELMo的权重施加了归纳偏置 λ \lambda λ,以保持接近所有biLM层的平均值。
(注:这里的增加ELMo的 dropout 率,不知道是为了防止BiLSTM的参数过拟合还是 s t a s k s^{task} stask 参数过拟合。以保持接近所有biLM层的平均值不知道是保持谁接近所有biLM层的平均值。)
3.4 Pre-trained bidirectional language model architecture
本文中预训练的BiLM与J o ˊ \acute{o} oˊzefowicz等人(2016)和Kim等人(2015)中的架构类似,但经过修改以支持双向联合训练,并在LSTM层之间添加residual connection(残差连接)。在这项工作中,我们将重点放在大规模BiLM上,Peters等人(2017)强调了使用BiLM而非仅向前LM,和大规模训练的重要性。
为了平衡整体语言模型的复杂性与下游任务的模型大小和计算要求,同时保持纯粹的基于字(character)的输入表示,我们将J o ˊ \acute{o} oˊzefowicz等人(2016年)的一个最佳模型CNN-BIG-LSTM的所有embedding维度和隐藏层维度减半。最终的模型使用 L = 2 L=2 L=2 个biLSTM层,具有4096个单元和512维度的投影,以及从第一层到第二层的residual connection(残差连接)。上下文不敏感类型的表示使用2048 个n-字(character n-gram) 卷积滤波器,后跟两个highway层(Srivastava et al.,2015)和降至512维表示的线性投影。因此,biLM为每个输入 token 提供了三层表示,包括那些由于保持纯粹的基于字(character)的输入,而在训练集之外的表示。相比之下,传统的word embedding方法只为固定词汇表中的 token 提供一层表示。
(注:这里三层表示应该指:上下文敏感类型表示和上下文不敏感类型表示,而上下文不敏感类型表示又分为:在训练集(2048 个n-字(character n-gram))之内和之外的纯粹的基于字(character)的表示。)
在1B Word Benchmark上进行了10个epoch的训练(Chelba等人,2014年),前向和后向困惑的平均值为39.7,而前向CNN-BIG-LSTM的平均值为30.0。一般来说,我们发现向前和向后的困惑大致相等,向后的值稍低。
一旦预训练,biLM可以计算任何任务的表示。在某些情况下,对特定领域数据的biLM进行微调会显著降低复杂性,并提高下游任务性能。这可以看作是biLM的一种表示域的转移。因此,在大多数情况下,我们在下游任务中使用了经过微调的biLM。详见补充资料。
相关视频
李宏毅-ELMO, BERT, GPT讲解:0:11:24 开始
相关的笔记
相关代码
pytorch
MorvanZhou /NLP-Tutorials:v_dim表示字典大小,units表示隐藏层的维度,2个LSTM层的softmax应该共享输出embedding,不应该使用2个输出embedding,即红色框应该只留一个。