【论文阅读笔记】darts代码和论文结合阅读

参考：https://zhuanlan.zhihu.com/p/73037439
注意：本篇都是分析的CNN部分，没有对RNN部分解读。
本篇文章主要通过代码对论文进行解读，darts就是对构成网络的cell的结构进行自动搜索，然后再将搜索到的cell 连接成一个网络。

introduction

differentiable architecture search

2.1 search space

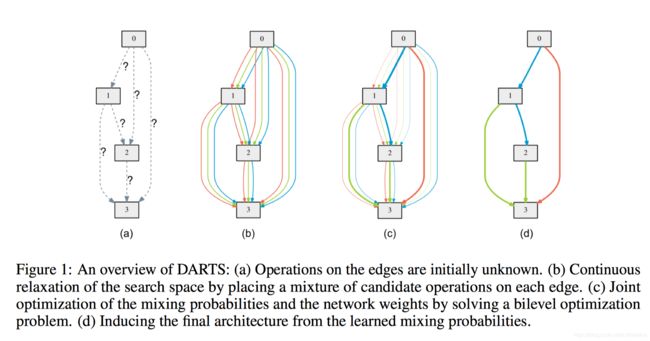
darts如何对一个cell进行搜索的呢，我们通过下图figure 1了解darts的基本思想：
(a)这些灰色的小方块都是一个cell内的nodes，我们需要通过一些操作（如池化、卷积）把这些nodes连起来
(b)原本一个个操作都是离散的，我们为了实现可微分的搜索，也就是为了使搜索空间连续，我们将特定操作的确定的选择放宽到所有可能操作上的softmax，也就是我们给两个block之间的全部操作都赋予权重。假设我们有三个操作，我们把每个节点都通过上述方法和它所有的前驱节点相连，就得到了下图(b)
©然后我们就通过梯度下降对权重进行优化，最后对每个节点取argmax也就是哪个操作的α值最大，就选这个操作。
(d)选了最大的α后的操作后，我们就得到了(d)的路径

具体的在CIFAR-10定义网络结构我们可以看下图：

一个Network是由8个cell组成的，cell分为reduction cell 和normal cell两种，在网络的三分之一处和三分之二处是reduction cell，其它是normal cell。reduction cell共享权重${\alpha }_{redution}$，normal cell共享权重${\alpha }_{normal}$。
一个cell由7个nodes组成，分别是2个input nodes，4个intermediate nodes和1个output nodes。

• input nodes：是前两层cell的输出，input node 0是cell k-2的输出，input node 1 是cell k-1的输出
• intermediate nodes：和它所有的前驱节点相连，具体看下面的公式
  对于节点$x^{(j)}$，通过操作o和它所有的前驱节点i相连，那么如何对操作o进行continuous relaxation，具体看2.2节
  
• output nodes：四个中间节点intermediate nodes concat，这个concat是对通道concat的，也就是原来输入的通道是C，输出以后变成了4C

model_search.py Class Cell

具体Cell是怎么定义的我们通过代码来看

class Cell(nn.Module):

  def __init__(self, steps, multiplier, C_prev_prev, C_prev, C, reduction, reduction_prev):
    super(Cell, self).__init__()
    self.reduction = reduction
    #input nodes的结构固定不变，不参与搜索
    #决定第一个input nodes的结构，取决于前一个cell是否是reduction
    if reduction_prev:
      self.preprocess0 = FactorizedReduce(C_prev_prev, C, affine=False)
    else:
      self.preprocess0 = ReLUConvBN(C_prev_prev, C, 1, 1, 0, affine=False)#第一个input_nodes是cell k-2的输出，cell k-2的输出通道数为C_prev_prev，所以这里操作的输入通道数为C_prev_prev
    #第二个input nodes的结构
    self.preprocess1 = ReLUConvBN(C_prev, C, 1, 1, 0, affine=False)#第二个input_nodes是cell k-1的输出
    self._steps = steps # 每个cell中有4个节点的连接状态待确定
    self._multiplier = multiplier

    self._ops = nn.ModuleList() # 构建operation的modulelist
    self._bns = nn.ModuleList()
    #遍历4个intermediate nodes构建混合操作
    for i in range(self._steps):
      #遍历当前结点i的所有前驱节点
      for j in range(2+i): #对第i个节点来说，他有j个前驱节点（每个节点的input都由前两个cell的输出和当前cell的前面的节点组成）
        stride = 2 if reduction and j < 2 else 1
        op = MixedOp(C, stride) #op是构建两个节点之间的混合
        self._ops.append(op)#所有边的混合操作添加到ops，list的len为2+3+4+5=14[[],[],...,[]]


  #cell中的计算过程，前向传播时自动调用
  def forward(self, s0, s1, weights):
    s0 = self.preprocess0(s0)
    s1 = self.preprocess1(s1)

    states = [s0, s1] #当前节点的前驱节点
    offset = 0
    #遍历每个intermediate nodes，得到每个节点的output
    for i in range(self._steps):
      s = sum(self._ops[offset+j](h, weights[offset+j]) for j, h in enumerate(states))  #s为当前节点i的output，在ops找到i对应的操作，然后对i的所有前驱节点做相应的操作（调用了MixedOp的forward），然后把结果相加
      offset += len(states)
      states.append(s)#把当前节点i的output作为下一个节点的输入
      #states中为[s0,s1,b1,b2,b3,b4] b1,b2,b3,b4分别是四个intermediate output的输出
    return torch.cat(states[-self._multiplier:], dim=1)#对intermediate的output进行concat作为当前cell的输出
                                                       #dim=1是指对通道这个维度concat，所以输出的通道数变成原来的4倍

2.2 continuous relaxation and optimization

为了使搜索空间连续，我们为每个操作都赋予一个权重$\alpha$，然后做softmax。这样搜索任务就简化为学习权重$\alpha$

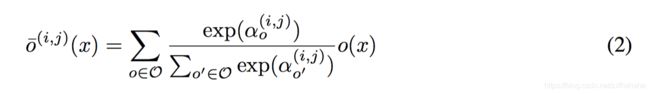
搜索完成后，我们通过argmax选权重最大的操作，这样就又得到了离散的结构，具体如下：
$o^{(i,j)=argma{x}_{o\in O}{\alpha }_0^{(i,j)}}$
argmax(f(x))是使得 f(x)取得最大值所对应的变量点x(或x的集合)，
也就是哪个操作对应的alpha取值最大，就取哪个操作.

model_search.py Class MixedOp

具体操作是如何混合的我们通过代码来看

class MixedOp(nn.Module):

  def __init__(self, C, stride):
    super(MixedOp, self).__init__()
    self._ops = nn.ModuleList()
    for primitive in PRIMITIVES:  #PRIMITIVES中就是8个操作
      op = OPS[primitive](C, stride, False)#OPS中存储了各种操作的函数
      if 'pool' in primitive:
        op = nn.Sequential(op, nn.BatchNorm2d(C, affine=False)) #给池化操作后面加一个batchnormalization
      self._ops.append(op)#把这些op都放在预先定义好的modulelist里

  def forward(self, x, weights):
    return sum(w * op(x) for w, op in zip(weights, self._ops))  #op(x)就是对输入x做一个相应的操作 w1*op1(x)+w2*op2(x)+...+w8*op8(x)
                                                                #也就是对输入x做8个操作并乘以相应的权重，把结果加起来

After relaxation, our goal is to jointly learn the architecture α and the weights w within all the mixed operations (e.g. weights of the convolution filters). Analogous to architecture search using RL or evolution where the validation set performance is treated as the reward or fitness, DARTS aims to optimize the validation loss, but using gradient descent.

在对操作relaxation之后，我们就要对$\alpha$和w进行学习，Darts是通过梯度下降优化validation loss来学习权重的。

Denote by $L_{train}$ and $L_{val}$ the training and the validation loss, respectively. Both losses are determined not only by the architecture α, but also the weights w in the network.
The goal for architecture search is to find ${\alpha }^{\ast }$ that minimizes the validation loss $L_{val}(w^{\ast },{\alpha }^{\ast })$, where the weights $w^{\ast }$ associated with the architecture are obtained by minimizing the training loss $w^{\ast }$ = $argmi{n}_w{L}_{train}(w,{\alpha }^{\ast })$.
This implies a bilevel optimization problem with α as the upper-level variable and w as the lower-level variable:

architecture search的目标就是通过最小化验证集的loss$L_{val}(w^{\ast },{\alpha }^{\ast })$得到α，而$w^{\ast }$又是通过最小化训练集loss得到的$w^{\ast }$ = $argmi{n}_w{L}_{train}(w,{\alpha }^{\ast })$。因此我们得到了如下的bilevel 公式：

2.3 approximate architecture gradient

本小节主要是在公式(3)和公式(4)的基础上做一个改进，首先作者提出了一个approximation scheme如下：

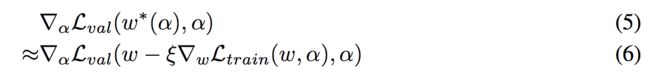
where w denotes the current weights maintained by the algorithm, and ξ is the learning rate for a step of inner optimization.
The idea is to approximate $w^{\ast }(\alpha )$ by adapting w using only a single training step, without solving the inner optimization (equation 4) completely by training until convergence.

我们用$w-\xi {▽}_w{L}_{train}(w,\alpha )$来近似$w^{\ast }(\alpha )$，这样只对w用了一次single training step，也就是达到了一步优化的效果，就不需要先对公式4进行优化，等收敛了再求α。

具体的伪代码如下：
也就是我们通过公式六对α值进行更新(对应代码中的architect.py)，然后再对网络的w进行更新。
伪代码中的两步详情见train_search.py中的train函数，

• 第一步对应architect.step(input, target, input_search, target_search, lr, optimizer, unrolled=args.unrolled)
  我们可以看到input_search和target search都是从valid_queue中拿出来的一个batch，也就对应了论文中说的用验证集对α进行更新
• 第二步对应logits = model(input)、loss = criterion(logits, target)、loss.backward()
  这里的input是训练集，因为w都是网络中定义的，loss.backward()就已经设计好了对网络的w进行更新

train_search.py def train

def train(train_queue, valid_queue, model, architect, criterion, optimizer, lr):
  objs = utils.AvgrageMeter() # 用于保存loss的值
  top1 = utils.AvgrageMeter() # 前1预测正确的概率
  top5 = utils.AvgrageMeter() # 前5预测正确的概率

  for step, (input, target) in enumerate(train_queue): #每个step取出一个batch，batchsize是64（256个数据对）
    model.train()
    n = input.size(0)

    input = Variable(input, requires_grad=False).cuda()
    target = Variable(target, requires_grad=False).cuda(async=True)

    # get a random minibatch from the search queue with replacement
    input_search, target_search = next(iter(valid_queue)) #用于架构参数更新的一个batch 。使用iter(dataloader)返回的是一个迭代器，然后可以使用next访问；
    input_search = Variable(input_search, requires_grad=False).cuda()
    target_search = Variable(target_search, requires_grad=False).cuda(async=True)
	
	#对α进行更新，对应伪代码的第一步，也就是用公式6
    architect.step(input, target, input_search, target_search, lr, optimizer, unrolled=args.unrolled)
	#对w进行更新，对应伪代码的第二步
    optimizer.zero_grad()#清除之前学到的梯度的参数
    logits = model(input)
    loss = criterion(logits, target) #预测值logits和真实值target的loss

    loss.backward()#反向传播，计算梯度
    nn.utils.clip_grad_norm(model.parameters(), args.grad_clip)#梯度裁剪
    optimizer.step() #应用梯度

    prec1, prec5 = utils.accuracy(logits, target, topk=(1, 5))
    objs.update(loss.data[0], n)
    top1.update(prec1.data[0], n)
    top5.update(prec5.data[0], n)

    if step % args.report_freq == 0:
      logging.info('train %03d %e %f %f', step, objs.avg, top1.avg, top5.avg)

  return top1.avg, objs.avg

We also note that when momentum is enabled for weight optimisation, the one-step unrolled learning objective in equation 6 is modified accordingly and all of our analysis still applies.
Applying chain rule to the approximate architecture gradient (equation 6) yields.

当应用Momentum时，作者通过链式法则对公式6进行修改，得到公式(7):

其中，$w^{\prime }=w-\xi {▽}_w{L}_{train}(w,\alpha )$。

公式6到公式7的推导

具体怎么通过链式法则把公式六变成公式7的呢，解释如下：

第一行的式子，实际上相当于是一个关于 [公式] 的复合函数求导，我们可以将其形式化记为：

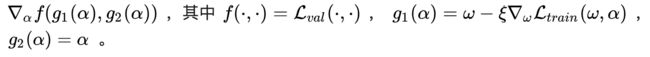
The expression above contains an expensive matrix-vector product in its second term. Fortunately, the complexity can be substantially reduced using the finite difference approximation.

又因为公式7的第二项包含一个复杂的matrix-vector product，所以我们通过对公式7进行有限差分近似得到公式8：

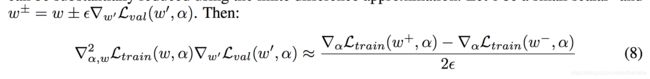
公式7到公式8的推导

从公式7到公式8主要是用下式，基本的泰勒展开：

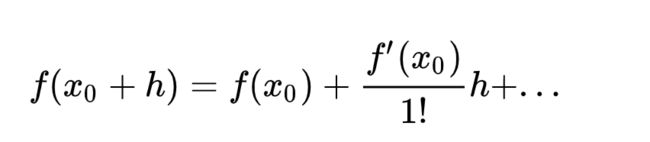
我们用hA替换上式的h，得到下式：

再将上面的两个式子相减，得到下式：

然后我们把h换成$ϵ$，把A换成$\xi {▽}_{w^{\prime }}{L}_{train}(w^{\prime },\alpha )$，把$x_0$换成w，再把f换成$\xi {▽}_{\alpha }{L}_{train}(\cdot ,\cdot )$，就得到公式8了。

architect.py

通过上面的部分我们知道更新$\alpha$是通过architect.step()来调用的，那么这个函数具体是怎么实现的，也就是上面讲的一大堆公式是怎么用的，我们一起来看一下architect.py的内容。

architect.step(input, target, input_search, target_search, lr, optimizer, unrolled=args.unrolled)

train_search.py的architect.step()调用architect.py中的step函数，下面是architect.py的解析：

import torch
import numpy as np
import torch.nn as nn
from torch.autograd import Variable


def _concat(xs):
  return torch.cat([x.view(-1) for x in xs]) #把x先拉成一行，然后把所有的x摞起来，变成n行


class Architect(object):

  def __init__(self, model, args):
    self.network_momentum = args.momentum
    self.network_weight_decay = args.weight_decay
    self.model = model
    self.optimizer = torch.optim.Adam(self.model.arch_parameters(),
        lr=args.arch_learning_rate, betas=(0.5, 0.999), weight_decay=args.arch_weight_decay) #用来更新α的optimizer

      """
    我们更新梯度就是theta = theta + v + weight_decay * theta 
      1.theta就是我们要更新的参数
      2.weight_decay*theta为正则化项用来防止过拟合
      3.v的值我们分带momentum和不带momentum：
        普通的梯度下降：v = -dtheta * lr 其中lr是学习率，dx是目标函数对x的一阶导数
        带momentum的梯度下降：v = lr*(-dtheta + v * momentum)
    """
    #【完全复制外面的Network更新w的过程】，对应公式6第一项的w − ξ*dwLtrain(w, α)
    #不直接用外面的optimizer来进行w的更新，而是自己新建一个unrolled_model展开，主要是因为我们这里的更新不能对Network的w进行更新
  def _compute_unrolled_model(self, input, target, eta, network_optimizer):
    loss = self.model._loss(input, target) #Ltrain
    theta = _concat(self.model.parameters()).data #把参数整理成一行代表一个参数的形式,得到我们要更新的参数theta
    try:
      moment = _concat(network_optimizer.state[v]['momentum_buffer'] for v in self.model.parameters()).mul_(self.network_momentum) #momentum*v,用的就是Network进行w更新的momentum
    except:
      moment = torch.zeros_like(theta) #不加momentum
    dtheta = _concat(torch.autograd.grad(loss, self.model.parameters())).data + self.network_weight_decay*theta #前面的是loss对参数theta求梯度，self.network_weight_decay*theta就是正则项
    #对参数进行更新，等价于optimizer.step()
    unrolled_model = self._construct_model_from_theta(theta.sub(eta, moment+dtheta))  #w − ξ*dwLtrain(w, α) 
                                                                                      
    return unrolled_model



  def step(self, input_train, target_train, input_valid, target_valid, eta, network_optimizer, unrolled):
    self.optimizer.zero_grad()#清除上一步的残余更新参数值
    if unrolled:#用论文的提出的方法
        self._backward_step_unrolled(input_train, target_train, input_valid, target_valid, eta, network_optimizer)
    else: #不用论文提出的bilevel optimization，只是简单的对α求导
        self._backward_step(input_valid, target_valid)
    self.optimizer.step() #应用梯度：根据反向传播得到的梯度进行参数的更新， 这些parameters的梯度是由loss.backward()得到的，optimizer存了这些parameters的指针
                          #因为这个optimizer是针对alpha的优化器，所以他存的都是alpha的参数

  def _backward_step(self, input_valid, target_valid):
    loss = self.model._loss(input_valid, target_valid)
    loss.backward() #反向传播，计算梯度

  
  def _backward_step_unrolled(self, input_train, target_train, input_valid, target_valid, eta, network_optimizer):
    #计算公式六：dαLval(w',α) ，其中w' = w − ξ*dwLtrain(w, α)
    #w'
    unrolled_model = self._compute_unrolled_model(input_train, target_train, eta, network_optimizer)#unrolled_model里的w已经是做了一次更新后的w，也就是得到了w'
    #Lval
    unrolled_loss = unrolled_model._loss(input_valid, target_valid) #对做了一次更新后的w的unrolled_model求验证集的损失，Lval，以用来对α进行更新
    
    unrolled_loss.backward()
    # dαLval(w',α)
    dalpha = [v.grad for v in unrolled_model.arch_parameters()] #对alpha求梯度
    # dw'Lval(w',α)
    vector = [v.grad.data for v in unrolled_model.parameters()] #unrolled_model.parameters()得到w‘
    #计算公式八(dαLtrain(w+,α)-dαLtrain(w-,α))/(2*epsilon)   其中w+=w+dw'Lval(w',α)*epsilon w- = w-dw'Lval(w',α)*epsilon
    implicit_grads = self._hessian_vector_product(vector, input_train, target_train)

    # 公式六减公式八 dαLval(w',α)-(dαLtrain(w+,α)-dαLtrain(w-,α))/(2*epsilon)
    for g, ig in zip(dalpha, implicit_grads):
      g.data.sub_(eta, ig.data)
    #对α进行更新
    for v, g in zip(self.model.arch_parameters(), dalpha):
      if v.grad is None:
        v.grad = Variable(g.data)
      else:
        v.grad.data.copy_(g.data)
  #对应optimizer.step()，对新建的模型的参数进行更新
  def _construct_model_from_theta(self, theta):
    model_new = self.model.new()
    model_dict = self.model.state_dict() #Returns a dictionary containing a whole state of the module.

    params, offset = {}, 0
    for k, v in self.model.named_parameters():#k是参数的名字，v是参数
      v_length = np.prod(v.size())
      params[k] = theta[offset: offset+v_length].view(v.size()) #将参数k的值更新为theta对应的值
      offset += v_length

    assert offset == len(theta)
    model_dict.update(params) #模型中的参数已经更新为做一次反向传播后的值
    model_new.load_state_dict(model_dict) #恢复模型中的参数，也就是我新建的mode_new中的参数为model_dict
    return model_new.cuda()

  
  #计算公式八(dαLtrain(w+,α)-dαLtrain(w-,α))/(2*epsilon)   其中w+=w+dw'Lval(w',α)*epsilon w- = w-dw'Lval(w',α)*epsilon
  def _hessian_vector_product(self, vector, input, target, r=1e-2): # vector就是dw'Lval(w',α)
    R = r / _concat(vector).norm() #epsilon

    #dαLtrain(w+,α)
    for p, v in zip(self.model.parameters(), vector):
      p.data.add_(R, v) #将模型中所有的w'更新成w+=w+dw'Lval(w',α)*epsilon
    loss = self.model._loss(input, target)
    grads_p = torch.autograd.grad(loss, self.model.arch_parameters())

    #dαLtrain(w-,α)
    for p, v in zip(self.model.parameters(), vector):
      p.data.sub_(2*R, v) #将模型中所有的w'更新成w- = w+ - (w-)*2*epsilon = w+dw'Lval(w',α)*epsilon - 2*epsilon*dw'Lval(w',α)=w-dw'Lval(w',α)*epsilon
    loss = self.model._loss(input, target)
    grads_n = torch.autograd.grad(loss, self.model.arch_parameters())

    #将模型的参数从w-恢复成w
    for p, v in zip(self.model.parameters(), vector):
      p.data.add_(R, v) #w=(w-) +dw'Lval(w',α)*epsilon = w-dw'Lval(w',α)*epsilon + dw'Lval(w',α)*epsilon = w

    return [(x-y).div_(2*R) for x, y in zip(grads_p, grads_n)]

2.4 deriving discrete architectures

通过上一节我们学到了alpha的值，这一节我们就是选出来α，把结构从连续的又变回离散的。

To form each node in the discrete architecture, we retain the top-2 strongest operations (from distinct nodes) among all non-zero candidate operations collected from all the previous nodes.

对每个node，我们都选alpha值的top2，这两个alpha要来自不同的节点，也就是你选的两个操作不能来自于同一个点。
这一步执行是在train_search.py的每个epoch都执行一次：

genotype = model.genotype() #对应论文2.4 选出来权重值大的两个前驱节点，并把(操作，前驱节点)存下来

model_search.py class Network def genotype

具体怎么做的在model_search.py的class Network 的函数genotype中，如下

  def genotype(self):
    def _parse(weights):
      gene = []
      n = 2
      start = 0
      for i in range(self._steps):
        end = start + n
        W = weights[start:end].copy()
        # 找出来前驱节点的哪两个边的权重最大
        edges = sorted(range(i + 2), key=lambda x: -max(W[x][k] for k in range(len(W[x])) if k != PRIMITIVES.index('none')))[:2]#sorted：对可迭代对象进行排序，key是用来进行比较的元素
                                                            # range(i + 2)表示x取0，1，到i+2 x也就是前驱节点的序号 ，所以W[x]就是这个前驱节点的所有权重[α0,α1,α2,...,α7]
                                                            # max(W[x][k] for k in range(len(W[x])) if k != PRIMITIVES.index('none')) 就是把操作不是NONE的α放到一个list里，得到最大值
                                                            # sorted 就是把每个前驱节点对应的权重最大的值进行逆序排序，然后选出来top2

        # 把这两条边对应的最大权重的操作找到
        for j in edges:
          k_best = None
          for k in range(len(W[j])):
            if k != PRIMITIVES.index('none'):
              if k_best is None or W[j][k] > W[j][k_best]:
                k_best = k
          gene.append((PRIMITIVES[k_best], j)) #把(操作，前驱节点序号)放到list gene中，[('sep_conv_3x3', 1),...,]
        start = end
        n += 1
      return gene

    gene_normal = _parse(F.softmax(self.alphas_normal, dim=-1).data.cpu().numpy()) #得到normal cell 的最后选出来的结果
    gene_reduce = _parse(F.softmax(self.alphas_reduce, dim=-1).data.cpu().numpy()) #得到reduce cell 的最后选出来的结果

    concat = range(2+self._steps-self._multiplier, self._steps+2) #[2,3,4,5] 表示对节点2，3，4，5 concat
    genotype = Genotype(
      normal=gene_normal, normal_concat=concat,
      reduce=gene_reduce, reduce_concat=concat
    )
    return genotype

experiments and results

In the first stage, we search for the cell architectures using DARTS, and determine the best cells based on their validation performance.
In the second stage, we use these cells to construct larger architectures, which we train from scratch and report their performance on the test set.

具体怎么训练的是分为两步进行的：

• 第一步：用darts进行architect search，通过validation performance选出来cells
  对应train_search.py
• 第二步：用选出来的cells构建网络，从头开始训练，报告他们在测试集上的表现
  对应train.py

3.1 architecture search

首先我们看一下我们的model是怎么构建的

model_search.py class Network

class Network(nn.Module):

  def __init__(self, C, num_classes, layers, criterion, steps=4, multiplier=4, stem_multiplier=3):
    super(Network, self).__init__()
    self._C = C #初始通道数
    self._num_classes = num_classes
    self._layers = layers
    self._criterion = criterion
    self._steps = steps #一个基本单元cell内有4个节点需要进行operation操作的搜索
    self._multiplier = multiplier

    C_curr = stem_multiplier*C # 当前Sequential模块的输出通道数
    self.stem = nn.Sequential(
      nn.Conv2d(3, C_curr, 3, padding=1, bias=False),  #前三个参数分别是输入图片的通道数，卷积核的数量，卷积核的大小
      nn.BatchNorm2d(C_curr) #BatchNorm2d对minibatch 3d数据组成的4d输入进行batchnormalization操作，num_features为(N,C,H,W)的C
    )
 
    C_prev_prev, C_prev, C_curr = C_curr, C_curr, C
    self.cells = nn.ModuleList()# 创建一个空modulelist类型数据
    reduction_prev = False #连接的前一个cell是否是reduction cell
    for i in range(layers): #网络是8层，在1/3和2/3位置是reduction cell 其他是normal cell，reduction cell的stride是2
      if i in [layers//3, 2*layers//3]: #对应论文的Cells located at the 1/3 and 2/3 of the total depth of the network are reduction cells
        C_curr *= 2
        reduction = True
      else:
        reduction = False
      #构建cell
      cell = Cell(steps, multiplier, C_prev_prev, C_prev, C_curr, reduction, reduction_prev)#每个cell的input nodes是前前cell和前一个cell的输出
      reduction_prev = reduction
      self.cells += [cell]
      C_prev_prev, C_prev = C_prev, multiplier*C_curr #C_prev=multiplier*C_curr是因为每个cell的输出是4个中间节点concat的，这个concat是在通道这个维度，所以输出的通道数变为原来的4倍

    self.global_pooling = nn.AdaptiveAvgPool2d(1) #构建一个平均池化层，output size是1x1
    self.classifier = nn.Linear(C_prev, num_classes) #构建一个线性分类器

    self._initialize_alphas()#架构参数初始化

        '''
    cell = Cell(steps, multiplier, C_prev_prev, C_prev, C_curr, reduction, reduction_prev)
    layers = 8, 第2和5个cell是reduction_cell
    cells[0]: cell = Cell(4, 4, 48,  48,  16, false,  false) 输出[N,16*4,h,w]
    cells[1]: cell = Cell(4, 4, 48,  64,  16, false,  false) 输出[N,16*4,h,w]
    cells[2]: cell = Cell(4, 4, 64,  64,  32, True,   false) 输出[N,32*4,h,w]
    cells[3]: cell = Cell(4, 4, 64,  128, 32, false,  false) 输出[N,32*4,h,w]
    cells[4]: cell = Cell(4, 4, 128, 128, 32, false,  false) 输出[N,32*4,h,w]
    cells[5]: cell = Cell(4, 4, 128, 128, 64, True,   false) 输出[N,64*4,h,w]
    cells[6]: cell = Cell(4, 4, 128, 256, 64, false,  false) 输出[N,64*4,h,w]
    cells[7]: cell = Cell(4, 4, 256, 256, 64, false,  false) 输出[N,64*4,h,w]
    '''

接下来看怎么对网络进行训练

train_search.py

1. 数据集
   用于architect search的数据集是CIFAR-10：
   training set: half of the CIFAR-10 training data
   validation set: another half of the CIFAR-10 training data
   其中sampler就体现了把training data的前一半用于training set，后一半用于validation set

  train_transform, valid_transform = utils._data_transforms_cifar10(args)
  train_data = dset.CIFAR10(root=args.data, train=True, download=True, transform=train_transform)

  num_train = len(train_data)
  indices = list(range(num_train))
  split = int(np.floor(args.train_portion * num_train))

  train_queue = torch.utils.data.DataLoader(
      train_data, batch_size=args.batch_size,
      sampler=torch.utils.data.sampler.SubsetRandomSampler(indices[:split]), #自定义从样本中取数据的策略，当train_portion=0.5时，就是前一半的数据用于train
      pin_memory=True, num_workers=2)

  valid_queue = torch.utils.data.DataLoader(
      train_data, batch_size=args.batch_size,
      sampler=torch.utils.data.sampler.SubsetRandomSampler(indices[split:num_train]), #数据集中后一半的数据用于验证
      pin_memory=True, num_workers=2)

2. 优化器optimizer
   <1> 用来优化w的优化器

  #设置优化器
  optimizer = torch.optim.SGD(
      model.parameters(),#优化器更新的参数，这里更新的是w
      args.learning_rate,#初始值是0.025，使用的余弦退火调度更新学习率，每个epoch的学习率都不一样
      momentum=args.momentum, #0.9
      weight_decay=args.weight_decay)#正则化参数3e-4
  #学习率更新参数，每次迭代调整不同的学习率
  scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(  #使用余弦退火调度设置各组参数组的学习率
        optimizer, float(args.epochs), eta_min=args.learning_rate_min)

<2> 用于优化α的优化器

    self.optimizer = torch.optim.Adam(self.model.arch_parameters(),
        lr=args.arch_learning_rate, betas=(0.5, 0.999), weight_decay=args.arch_weight_decay) #用来更新α的optimizer

3. 每个epoch进行train和infer

model = Network(args.init_channels, CIFAR_CLASSES, args.layers, criterion)#构建网络

  #创建用于更新α的architect
  architect = Architect(model, args)
  #经历50个epoch后搜索完毕
  for epoch in range(args.epochs):
    scheduler.step()
    lr = scheduler.get_lr()[0] #得到本次迭代的学习率lr
    logging.info('epoch %d lr %e', epoch, lr)

    genotype = model.genotype() #对应论文2.4 选出来权重值大的两个前驱节点，并把最后的结果存下来，格式为Genotype(normal=[(op,i),..],normal_concat=[],reduce=[],reduce_concat=[])
    logging.info('genotype = %s', genotype)

    print(F.softmax(model.alphas_normal, dim=-1))
    print(F.softmax(model.alphas_reduce, dim=-1))

    # training
    train_acc, train_obj = train(train_queue, valid_queue, model, architect, criterion, optimizer, lr)
    logging.info('train_acc %f', train_acc)

    # validation
    valid_acc, valid_obj = infer(valid_queue, model, criterion)
    logging.info('valid_acc %f', valid_acc)

    utils.save(model, os.path.join(args.save, 'weights.pt'))

   

<1>训练train

def train(train_queue, valid_queue, model, architect, criterion, optimizer, lr):
  objs = utils.AvgrageMeter() # 用于保存loss的值
  top1 = utils.AvgrageMeter() # 前1预测正确的概率
  top5 = utils.AvgrageMeter() # 前5预测正确的概率

  for step, (input, target) in enumerate(train_queue): #每个step取出一个batch，batchsize是64（256个数据对）
    model.train()
    n = input.size(0)

    input = Variable(input, requires_grad=False).cuda() #requires_grad为false不对input求导
    target = Variable(target, requires_grad=False).cuda(async=True)

    # get a random minibatch from the search queue with replacement
    # 更新α是用validation set进行更新的，所以我们每次都从valid_queue拿出一个batch传入architect.step()
    input_search, target_search = next(iter(valid_queue)) # 使用iter(dataloader)返回的是一个迭代器，然后可以使用next访问；
    input_search = Variable(input_search, requires_grad=False).cuda()
    target_search = Variable(target_search, requires_grad=False).cuda(async=True)

    #更新α
    architect.step(input, target, input_search, target_search, lr, optimizer, unrolled=args.unrolled) #unrolled是true就是用论文的公式进行α的更新

    optimizer.zero_grad()#清除之前学到的梯度的参数
    logits = model(input)
    loss = criterion(logits, target) #预测值logits和真实值target的loss

    loss.backward()#反向传播，计算梯度
    nn.utils.clip_grad_norm(model.parameters(), args.grad_clip)#梯度裁剪
    optimizer.step() #应用梯度

    prec1, prec5 = utils.accuracy(logits, target, topk=(1, 5))
    objs.update(loss.data[0], n)
    top1.update(prec1.data[0], n)
    top5.update(prec5.data[0], n)

    if step % args.report_freq == 0:
      logging.info('train %03d %e %f %f', step, objs.avg, top1.avg, top5.avg)

  return top1.avg, objs.avg

<2> 验证 infer
只前向传播
也就是上一步train完model的参数已经更新了，我们就在验证集上前向传播一次求一下loss，看一下好坏

#只前向传播
def infer(valid_queue, model, criterion):
  objs = utils.AvgrageMeter()
  top1 = utils.AvgrageMeter()
  top5 = utils.AvgrageMeter()
  model.eval()

  for step, (input, target) in enumerate(valid_queue):
    input = Variable(input, volatile=True).cuda()
    target = Variable(target, volatile=True).cuda(async=True)

    logits = model(input)
    loss = criterion(logits, target)

    prec1, prec5 = utils.accuracy(logits, target, topk=(1, 5))
    n = input.size(0)
    objs.update(loss.data[0], n)
    top1.update(prec1.data[0], n)
    top5.update(prec5.data[0], n)

    if step % args.report_freq == 0:
      logging.info('valid %03d %e %f %f', step, objs.avg, top1.avg, top5.avg)

  return top1.avg, objs.avg

utils.py

求精度具体的操作：

def accuracy(output, target, topk=(1,)):  #output:(bs,num_class)是64行10列, target:(bs,1)，topk=(1,5)
  maxk = max(topk) #5
  batch_size = target.size(0)

  _, pred = output.topk(maxk, 1, True, True)#maxk=5，表示dim=1按行取值
                                            #output的值是精度，选top5是选这一行精度最大的五个对应的列，也就是属于哪一类
                                            #pred是(bs,5) 值为类别号，0，1，...,9      
  pred = pred.t() #转置，pred:(5,bs)
  correct = pred.eq(target.view(1, -1).expand_as(pred)) #pred和target对应位置值相等返回1，不等返回0
                                                        #target原来是64行1列，值为类别；target.view(1, -1)把target拉成一行，expand_as(pred)又把target变成5行64列
  res = []
  for k in topk:# k=1和k=5
    correct_k = correct[:k].view(-1).float().sum(0)
    res.append(correct_k.mul_(100.0/batch_size))
  return res #res里是两个值，一个是top1的概率，一个是top5的概率

3.2 architecture evaluation

To evaluate the selected architecture, we randomly initialize its weights (weights learned during the search process are discarded), train it from scratch, and report its performance on the test set.

architecture evaluation这一部分做的就是把architecture search 部分搜到的cell 拿过来（normal cell 和reduction cell的权重），从头进行训练一下。这就和我们之前的那种train大同小异，就是网络结构定好了。

他说的随机初始化的权重不包括α。

train.py

这一部分和train_search.py的区别就是没有α那部分了，直接把α拿过来用

def main():
  if not torch.cuda.is_available():
    logging.info('no gpu device available')
    sys.exit(1)

  np.random.seed(args.seed)
  torch.cuda.set_device(args.gpu)
  cudnn.benchmark = True
  torch.manual_seed(args.seed)
  cudnn.enabled=True
  torch.cuda.manual_seed(args.seed)
  logging.info('gpu device = %d' % args.gpu)
  logging.info("args = %s", args)

  #得到train_search里学好的normal cell 和reduction cell，genotypes.DARTS就是选的学好的DARTS_V2
  genotype = eval("genotypes.%s" % args.arch) #DARTS_V2 = Genotype(normal=[('sep_conv_3x3', 0), ('sep_conv_3x3', 1), ('sep_conv_3x3', 0), ('sep_conv_3x3', 1), ('sep_conv_3x3', 1), ('skip_connect', 0), ('skip_connect', 0), ('dil_conv_3x3', 2)], normal_concat=[2, 3, 4, 5], reduce=[('max_pool_3x3', 0), ('max_pool_3x3', 1), ('skip_connect', 2), ('max_pool_3x3', 1), ('max_pool_3x3', 0), ('skip_connect', 2), ('skip_connect', 2), ('max_pool_3x3', 1)], reduce_concat=[2, 3, 4, 5])

  #这里的Network用的是model.py的NetworkCIFAR
  model = Network(args.init_channels, CIFAR_CLASSES, args.layers, args.auxiliary, genotype)
  model = model.cuda()

  logging.info("param size = %fMB", utils.count_parameters_in_MB(model))

  criterion = nn.CrossEntropyLoss()
  criterion = criterion.cuda()
  optimizer = torch.optim.SGD(
      model.parameters(),
      args.learning_rate,
      momentum=args.momentum,
      weight_decay=args.weight_decay
      )

  train_transform, valid_transform = utils._data_transforms_cifar10(args)
  train_data = dset.CIFAR10(root=args.data, train=True, download=True, transform=train_transform)
  valid_data = dset.CIFAR10(root=args.data, train=False, download=True, transform=valid_transform)

  train_queue = torch.utils.data.DataLoader(
      train_data, batch_size=args.batch_size, shuffle=True, pin_memory=True, num_workers=2)

  valid_queue = torch.utils.data.DataLoader(
      valid_data, batch_size=args.batch_size, shuffle=False, pin_memory=True, num_workers=2)

  scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, float(args.epochs))

  for epoch in range(args.epochs):
    scheduler.step()
    logging.info('epoch %d lr %e', epoch, scheduler.get_lr()[0])
    model.drop_path_prob = args.drop_path_prob * epoch / args.epochs

    train_acc, train_obj = train(train_queue, model, criterion, optimizer)
    logging.info('train_acc %f', train_acc)

    valid_acc, valid_obj = infer(valid_queue, model, criterion)
    logging.info('valid_acc %f', valid_acc)

    utils.save(model, os.path.join(args.save, 'weights.pt'))

model.py

model和model_search的区别也就在于cell 部分是把学到的权重直接拿来建网络

class Cell(nn.Module):

  def __init__(self, genotype, C_prev_prev, C_prev, C, reduction, reduction_prev):
    super(Cell, self).__init__()
    print(C_prev_prev, C_prev, C)

    if reduction_prev:
      self.preprocess0 = FactorizedReduce(C_prev_prev, C)
    else:
      self.preprocess0 = ReLUConvBN(C_prev_prev, C, 1, 1, 0)
    self.preprocess1 = ReLUConvBN(C_prev, C, 1, 1, 0)
    
    #这一部分就是根据是reduction cell 还是normal cell 把对应的节点和节点的操作找到
    if reduction:
      op_names, indices = zip(*genotype.reduce)
      concat = genotype.reduce_concat
    else:
      op_names, indices = zip(*genotype.normal)
      concat = genotype.normal_concat
    self._compile(C, op_names, indices, concat, reduction)

  def _compile(self, C, op_names, indices, concat, reduction):
    assert len(op_names) == len(indices)
    self._steps = len(op_names) // 2
    self._concat = concat
    self.multiplier = len(concat)

    self._ops = nn.ModuleList()
    for name, index in zip(op_names, indices):
      stride = 2 if reduction and index < 2 else 1
      op = OPS[name](C, stride, True)
      self._ops += [op]
    self._indices = indices

具体训练的细节：

A large network of 20 cells is trained for 600 epochs with batch size 96. The initial number of channels is increased from 16 to 36 to ensure our model size is comparable with other baselines in the literature (around 3M).
Other hyperparameters remain the same as the ones used for architecture search.

conclusion