推荐算法-PNN(Product Network)

推荐算法-PNN

  这篇文章出自上海交大，针对直接把Embedding之后的特征输入到神经网络中进行计算对特征的交叉组合不充分而提出来的。也是对特征的组合做文章的一种方法。

PNN网络结构

  模型结构如下图所示：

可以看出模型也是实现CTR预估任务，输入数据是对特征进行one-hot编码之后特征，然后经过一个embedding层，将输入特征映射到相同长度的特征得到上图中的embedding层，接下来就是Product Layer了。Product layer主要有两部分，一部分是线性部分z，另一部分是非线性组合部分p。得到这一部分的特征之后，就进行常规的深度学习部分了，经过两个隐藏层，然后直接输入CTR结果。本文的重点是Product Layer部分。

Product Layer

  Product layer部分的思想是认为特征之间的关系是and“且”的一种关系，而非add"加"的关系。以往的方法中特征之间都是$w_i\ast x_i+w_j\ast x_j$的组合方式，这种组合方式过于简单而且是不能凸显出特征之间紧密关系。举个例子：性别为男且喜欢打游戏的人 和 性别为男和喜欢打游戏的人，两者表达的是不同的意思。前者把特征更加细化，相当于抽取的特征更加“明显”或者"精细"，但是后者抽取的特征还是比较跨宽泛的表示。因此后者更能体现特征交叉组合的意义。
  再看上图，product layer部分包含两部分，第一部分是z，第二部分是p。虽然这一层的特征都是圆圈来表示，但是意义却大不相同。首先看z部分，这一块是线性部分，其实就相当与把Embedding层的特征拿过来，组成一个向量即可。
$$z=concat([em{b}_1,em{b}_2..,em{b}_n],axis=1)$$所以上图中的每一个圆圈代表的是一个向量（每一个field特征的embedding表示）。
  接着看p部分，p这一块有两种表示，分别为内积和外积。内积用IPNN表示，外积用OPNN表示。听名字还是很好理解的，就是向量的内积和外积。

IPNN部分

  IPNN就是实现两个向量的点乘，得到的是一个数，思路就是将所有field的embedding表示两两相乘，可以得到一个长度为$field\_size\ast (field\_size-1)/2$的向量p，然后将这个向量p与前面的线性部分z 拼接起来得到一组完整的向量，送入到下一层隐藏层。再这一块实现向量两两相乘的时候，我竟然天正的想着用for循环来实现，后来参考了作者的源代码，才发现tf的美好之处，后面会讲到的。

OPNN部分

  OPNN部分就是实现两个向量的外积，得到一个矩阵。所以此时上面图中p部分的每一个圆圈代表一个矩阵。但是矩阵怎么和z部分的向量拼接呢，作者在这里引入了科可学习的参数，矩阵$w$。表达式为$$U^{T}V\ast W=U\ast W\ast V^T$$上面$U、V$分别表示特征的embedding表示，大小为$embedding\_size\ast 1$，$w$表示矩阵大小为$embedding\_size\ast embedding\_size$，通过对等式左边进行变换得到右边的表达式，这样会降低复杂度。两个向量外积之后得到的矩阵大小为$embedding\_size\ast embedding\_size$，因此矩阵$w$的大小也是这样。矩阵$w$与外积得到的矩阵进行对应位置相乘再相加得到一个标量。因此OPNN时也是先将特征的embedding表示两两相乘，得到$field\_size\ast (field\_size-1)/2$个矩阵，然后利用$w$矩阵和其相乘，最终得到一组向量，再与线性部分z拼接。送入隐藏层。

  所以不管是IPNN和OPNN，送入隐藏层的特征长度为线性部分z的长度加非线性部分p的长度$embedding\_size\ast field\_size+field\_size\ast (field\_size-1)/2$。线性部分的长度就是所有field的embedding部分拼接起来。

实现过程

  实现过程相对来说比较简单，数据预处理部分与前面几篇文章的处理方法一样，本篇不再详细介绍。直接进入模型部分：
  首先是权重部分，权重部分包括embedding部分、product layer部分如果是内积的话是没有权重的，如果是外积的话是包括权重的、最后还有全连接部分的权重。embedding部分的权重很简单，要看输入不同field部分的特征one-hot编码之后的长度featuresize，以及embedding的长度，这部分权重的shape=[featuresize,embeddingsize]。然后是product部分的权重，这部分权重是外积的时候使用的，前面提到外积是生成一个$embedding\_size\ast embedding\_size$大小的矩阵，共有$pairs=field\_size\ast (field\_size-1)/2$个矩阵，因此这部分的权重shape=[embedding_size, pairs, embedding_size]，pairs放在中间是为了后面计算方便。embedding部分权重如下：

        weights['feature_embeddings'] = tf.Variable(
            tf.random_normal(shape=(self.featureSize, self.embeddingSize), mean=0.0, stddev=0.001,
                             name='feature_embeddings')
        )

        weights['feature_bias'] = tf.Variable(
            tf.random_normal(shape=(self.featureSize, 1), mean=0.0, stddev=0.001,
                             name='feature_bias')
        )

product部分权重如下：

        # product layer
        if self.useInner:
            pass
        else:
            weights['product_quadratic_outer'] = tf.Variable(
                tf.random_normal(shape=[self.embeddingSize, self.pairs, self.embeddingSize], mean=0.0, stddev=0.001),
                name='product_quadratic_outer')

然后是全连接的权重：

        # 全连接层输入长度
        inputSize = self.embeddingSize * self.fieldSize + self.pairs

        # deep layer
        weights['layer_0'] = tf.Variable(
            tf.random_normal(shape=[inputSize, self.deepLayers[0]], mean=0.0, stddev=0.001, name='layer_0')
        )
        weights['bias_0'] = tf.Variable(
            tf.random_normal(shape=[1, self.deepLayers[0]])
        )

        for i in range(1, len(self.deepLayers)):
            weights['layer_{}'.format(i)] = tf.Variable(tf.random_normal(shape=[self.deepLayers[i-1], self.deepLayers[i]],
                                                                         mean=0.0, stddev=0.001), name='layer_{}'.format(i))
            weights['bias_{}'.format(i)] = tf.Variable(tf.random_normal(shape=[1, self.deepLayers[i]], mean=0.0,
                                                                        stddev=0.001), name='bias_{}'.format(i))

        weights['output'] = tf.Variable(tf.random_normal(shape=[self.deepLayers[-1], 1], mean=0.0, stddev=0.001), name='output')
        weights['out_bias'] = tf.Variable(tf.random_normal(shape=[1]), name='output_bias')

  计算图的构建，这一部分就是构建整个模型的结构。embedding部分很简单，然后还有线性部分的z，以及非线性部分的p，p分为内积和外积。
输入数据的设置：

        weights = self._initWeights()

        self.featIndex = tf.placeholder(shape=[None, None], dtype=tf.int32, name='featIndex')
        self.featValue = tf.placeholder(shape=[None, None], dtype=tf.float32, name='featValue')
        self.label = tf.placeholder(shape=[None, 1], dtype=tf.float32, name='label')
        self.dropoutKeep = tf.placeholder(shape=[None], name='dropoutKeep', dtype=tf.float32)
        self._trainPhase = tf.placeholder(tf.bool, name='train_phase')

embedding部分：

        # Embedding

        self.embeddings = tf.nn.embedding_lookup(weights['feature_embeddings'], self.featIndex)  # N * F * K
        featValue = tf.reshape(self.featValue, shape=[-1, self.fieldSize, 1])  # N * F * 1
        self.embeddings = tf.multiply(self.embeddings, featValue)  # N * F * K

product layer的z部分：

        lz = tf.reshape(self.embeddings, shape=(-1, self.fieldSize*self.embeddingSize))

接下来就是p部分，这里需要对向量进行两两相乘，开始没有想起来很好的办法，然后参考了一下源代码，瞬间就明白了。先看一个小例子：

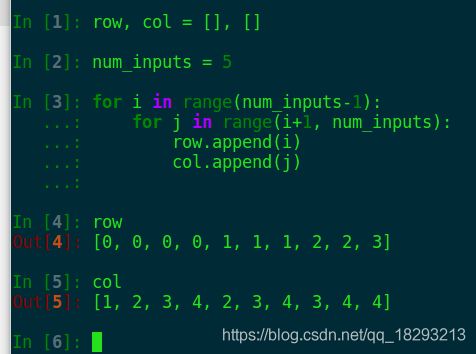
看这个例子应该能明白了吧，比如说我们一共有[0, 1, 2, 3, 4]5个数，要实现两两的乘法，那么我们把这些数先找出来，乘号左边的存在row中，乘号右边的存在col中。找出来这些数字，就可以实现相互乘法了。现在先找出来互相乘的索引，然后生成对应的矩阵即可了。
内积部分：

        if self.useInner:  # 内积
            row = []
            col = []

            for i in range(self.fieldSize-1):
                for j in range(i+1, self.fieldSize):
                    row.append(i)
                    col.append(j)

            p = tf.transpose(
                tf.gather(
                    tf.transpose(self.embeddings, [1, 0, 2]),
                    row),
                [1, 0, 2])

            q = tf.transpose(
                tf.gather(
                    tf.transpose(self.embeddings, [1, 0, 2]),
                    col),
                [1, 0, 2])
            # batch * pair * embedding
            p = tf.reshape(p, [-1, self.pairs, self.embeddingSize])
            q = tf.reshape(q, [-1, self.pairs, self.embeddingSize])
            self.lp = tf.reshape(tf.reduce_sum(p*q, [-1]), [-1, self.pairs])

外积部分：
外积本来是$U^{T}V\ast W｝$但是这样计算复杂度有些高，所以改成$U\ast W{V}^T$，U的shape为[batch, pair, k] W的shape为[k, pair, k]，为了实现U和W的相乘，首先要对U的shape调整为[batch, 1, pair, k]，然后二者再相乘，最后再和V相乘。

        else:  # 外积
            # (batch * pair * k) * (batch * k * pair) * (batch * k * k)
            row = []
            col = []

            for i in range(self.fieldSize-1):
                for j in range(i+1, self.fieldSize):
                    row.append(i)
                    col.append(j)

            p = tf.transpose(
                tf.gather(
                    tf.transpose(self.embeddings, [1, 0, 2]),
                    row),
                [1, 0, 2])

            q = tf.transpose(
                tf.gather(
                    tf.transpose(self.embeddings, [1, 0, 2]),
                    col),
                [1, 0, 2])
            p = tf.expand_dims(p, axis=1)  # batch * 1 * pair * k
            # batch * pair
            self.lp = tf.reduce_sum(
                # batch * pair * k
                tf.multiply(
                    # batch * pair * k
                    tf.transpose(
                        # batch * k * pair
                        tf.reduce_sum(
                            # (batch * 1 * pair * k) (k * pair * k)
                            tf.multiply(p, weights['product_quadratic_outer']),
                            axis=-1),
                        [0, 2, 1]),
                    q),
                axis=-1)

全连接层部分：
直接将线性部分的z和非线性部分的p 拼接起来，然后进行全连接层的计算。

        l = tf.concat([lz, self.lp], axis=1)

        # deep 部分
        for i in range(len(self.deepLayers)):
            l = tf.matmul(l, weights['layer_{}'.format(i)]) + weights['bias_{}'.format(i)]
            l = self.deepLayerActivation(l)
            l = tf.nn.dropout(l, self.dropoutKeep[i+1])
        self.out = tf.add(tf.matmul(l, weights['output']), weights['out_bias'])

＆emsp; 这篇文章的思路就是实现特征的两两之间的组合，通过两种不同的方式（内积和外积），并且保留了原始的线性部分（embedding部分），最后经过几层全连接层输出ctr结果。

参考

https://blog.csdn.net/u010352603/article/details/82670323

https://github.com/Atomu2014/product-nets