时序图文献精度——3.2019-NeurlPS-Self-attention with Functional Time Representation Learning
Self-attention with Functional Time Representation Learning
1.Abstract
为了弥合建模时间无关和时间相关事件序列之间的差距,作者引入了一个功能特征图,将时间跨度嵌入到高维空间中。通过构造相应的平移不变时间核函数,揭示了经典函数分析结果,即Bochner定理和Mercer定理下特征映射的函数形式。我们提出了几个模型来学习函数时间表示以及与事件表示的交互。
2.Introduction
时间嵌入提出的原因:停留时间通常表示对网页的兴趣程度,而顺序信息只考虑过去浏览的顺序。此外,检测时间和事件上下文之间的相互作用是用户行为建模中一个越来越重要的主题。在网上购物中,交易通常表明长期利益,而观点通常是短期的。因此,未来的建议应该同时依赖于事件上下文和事件发生的时间戳。
考虑用一些函数映射替换位置编码是很自然和直接的,这些函数映射将时间嵌入到向量空间中
与位置编码不同(位置编码只需要有限数量的索引表示),时间跨度是一个连续变量。
时间嵌入面临的三个挑战:
- 需要确定合适的以时间跨度为输入的函数形式。
- 函数形式必须适当参数化,并可以作为模型的一部分进行联合优化。
- 嵌入的时间表示应该尊重时间本身的函数属性
3.preliminary
Self-Attention
自我注意力机制一般由两部分构成:嵌入层和自我注意力层。
自我注意力使用位置编码来对位置信息建模,即每个位置k都表示一个向量p_k。
对一个有序实体序列e = (e_1,…,e_l),嵌入层使用实体嵌入(或特征)及其位置编码的加和或连接作为输入:
![]()
目标是得到一个从时间域到d_T维向量空间的连续函数映射,来代替式(1)中的位置编码。对序列中的第k个实体,用一个时间特征t_k得到的Φ(t_k)来代替向量p_k。
将学习时间模式的任务转换为一个以Φ为特征映射的核学习问题。此外,事件嵌入和时间之间的交互现在可以通过其他一些映射来识别。我们希望识别出一些与当前深度学习框架兼容的函数形式的Φ,这样通过晒传播计算仍然是可行的。
受Bochner’s theorem的启发,文章认为任何关于时间的周期函数都能展开成傅立叶级数,则有定理1如下。
Bochner’s Theorem
一个连续且平移不变的核函数K(x,y) = ψ(x-y)在R上是正定的,当且仅当R上存在一个非负测度,使得ψ为该测度的傅里叶变换。因此,在适当缩放时,时序核函数K具有替代表达式,即

其中ξ_w(t)=e^ (iwt),有欧拉公式为e^ix = cosx + isinx。由于K和概率测度p(w)为实数,此处提取实数部分,即只保留cosx,从而由式(2)推导至(3)。
![]()
有w1,…,wd为p(w)的独立同分布,因此可以得到有限维的函数映射如下,且易得近似关系有:
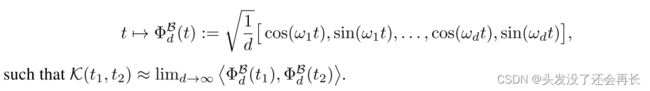
事实上,仅需合理数量的样本即可实现正确的估算,有声明1如下。
Claim1
有效学习波赫纳定理提出的特征映射的一个实际解决方案是使用“重新参数化技巧”。
设p(w)为Bochner定理中针对核函数K所述的相应概率测度,假设使用样本{wi}^d如上所述构建特征映射Φ,则只需d个样本就有:
![]()
其中σ是关于p(w)的第二动量(可理解为梯度优化的速度向量),有d为:

因而,可以将核函数学习转化为分布学习的问题,即评估p(w)。
一个直接的解决方案是,通过使用具有已知边际分布的辅助随机变量来应用重新参数化技巧,如在变分自编码器中一样,但再参数化往往受到分布规模的限制。另一种方法是使用逆累积分布函数(CDF)转换,该方法通过学习由基于流的网络参数化的逆累积分布函数,并从相应分布中抽取样本。
另一方面,如果我们考虑无参数化方法来估算分布,那么学习到的F^-1及从中得到的d个样本就等同于直接优化式(4)中的{w1,…,wd}作为自由模型参数。
事实上这两种方法具有相似的高性能,因此本文主要关注于无参数化方法,因为其参数更有效且训练速度更快。这种函数时序编码可以与自我注意力机制很好地结合,因此就能够用其来代替式(1)中的位置编码。
4.Conclusion
作者提出了一套用于函数时间表示学习的时间嵌入方法,并证明了其在连续时间事件序列预测中与自注意结合使用的有效性。所提出的方法具有合理的理论依据,它们不仅揭示了时间模式,而且还捕捉了时间-事件的相互作用。
文章意图将自注意力机制中的位置编码替换为时间编码,通过自注意力机制可以将节点的邻居信息按照时间顺序进行权重赋值等操作,并最终与节点自身信息相结合,得到节点在任意时间点的嵌入。
文章基于Bochner理论和Mercer理论,提出了两类时间编码算法。
对Bochner理论,算法用核函数替换时间编码函数,并使用傅里叶变换、欧拉公式、蒙特卡洛积分进行推导,问题变为学习频率分布,进而介绍了参数化和无参数化的方法。
对Mercer理论,用核函数替换时间编码函数,再将未知的核函数映射为一组与其有相同性质的核函数。
参考文章:
文献阅读(11)ICLR2020-Inductive representation learning on temporal graphs
文献阅读(18)NIPS2019-Self-attention with Functional Time Representation Learning