matlab偏微分方程数值解误差_机器学习偏微分方程的差分近似
之前介绍的 Physics Informed Deep Learning 解偏微分方程时都是使用深度神经网络得到一个参数化的解,然后通过最小化解对初始条件,边界条件以及偏微分方程的破坏程度,训练学习得到近似解的参数。缺点是对每一个初始条件都要重新训练一次神经网络。
今天介绍一个使用神经网络解偏微分方程的新思路。这种方法训练一次神经网络之后,可能适用于不同的初始条件。具体方法是对给定的偏微分方程,学习最好的差分近似离散化方案。此离散化方案依赖于具体的偏微分方程,时空格点以及场量的局域变化曲率。
Learning data driven discretizations for partial differential equationsarxiv.org结果
专业术语的解释放在方法部分。
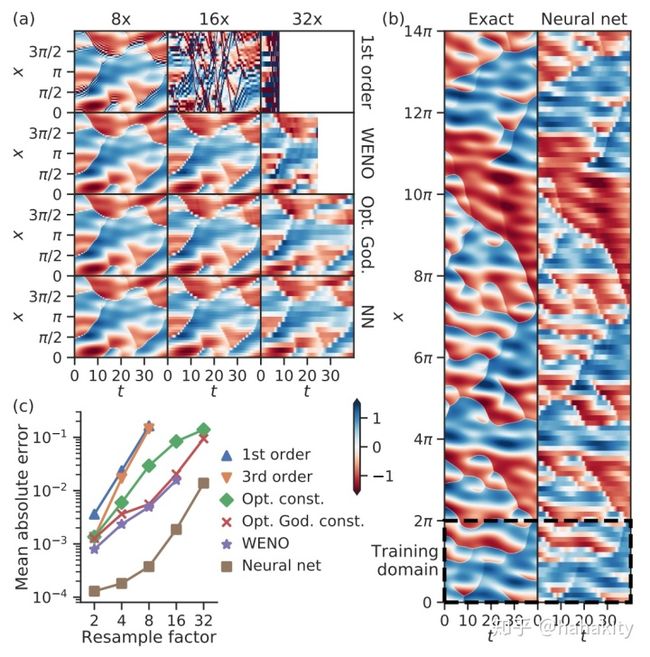
文章图(a) 在格子16倍粗粒化时,1阶迎风(1st order)算法已经发散;放大32倍时,WENO算法在第20个时间步也开始发散,而神经网络提供的差分离散化方案一直到第40个时间步都工作正常。
文章图 (b) 对比了7个区域的精确解与神经网络解在40个时间步长上的演化,结果还算比较精确。横轴是时间。
图(c), 定量对比了不同算法的平均绝对误差,发现在32倍粗粒化时,传统方法的误差是神经网络解的 10 倍。
方法
好的离散化方案应该类似于重整化群,在更粗粒度的离散化方案中得到细粒度下物理的有效近似。在流体力学里面,这相当于将高频信号和局部涨落积分,得到系统的长波近似。在光学中,当系统尺度远大于光的波长,几何光学也是对麦克斯韦方程组的很好近似。所以,如果神经网络能够在粗粒度下学到对底层微观动力学的有效近似,可以解决很多问题。
多体系统的涌现(集体)现象需要微观机制,但如果从第一原理即微观机制出发,模拟整个物理系统,则会受到很多非相关细节的干扰。如何构造粗粒度下的有效理论近似微观机制的集体效应,可能推动整个物理学领域的发展。重整化群即是这样一种思想。本文立意很高,试图使用神经网络学到粗粒化的差分离散化方案,有效近似微观动力学带来的宏观效应。
差分近似入门
如果我们要数值求解下面这个偏微分方程(假设v是常数),该怎么做?
这个方程告诉我们,流体密度
如果将
如果将 x 离散化为
相应的就有
根据泰勒展开,
可以知道
对 x 的偏微分用同样的方法化为差分,得到这一章最开头的偏微分方程最简单的离散化形式为,
简化一下,将 n+1 时刻需要计算的量放左边,将 n 时刻所有已知的量移到右边,得到
初始条件
差分近似进阶
可能你会觉得差分近似太简单了,一看就会。但现实情况是一用就错。
比如上面这个差分近似,如果常数
注意上节末尾为了计算 i 点的空间微分,使用了 (i+1, i) 两个格点的信息;而迎风格式使用了 (i-1, i) 两个格点的信息。就这一点点不同,导致迎风格式收敛,而另一个发散。最直观的理解是,当 v>0 时,信息从左往右传播,计算 i 点的微分使用 i+1 点的流体密度违背了因果律。
为何 (i-1, i) 两点也能用来计算空间的偏微分呢?还是泰勒展开,
同样可以得到
这里的迎风格式还是一阶精度,即近似到
如何得到更高精度的差分近似呢?泰勒展开到更高阶,联立求解便是!
都展开到二阶的时候,两个相减则得到,
这种差分方案称作中心差分,具有二阶精度。
将两者相加,消掉 f 的一阶偏导,则可以得到二阶微分的差分形式,
同理,对
微分的差分近似很像卷积核,比如这个二阶微分,化为卷积操作则系数为,
将这个卷积核从左到右点乘到
有限体积法
有限体积法使用每个格子内部场量的积分平均值来代替格子边界上的值,更好的保证物理量的守恒。本质上与有限差分法没有太大区别。
本文做法
上文所示差分离散化方案一般是人为指定的,在数值求解偏微分方程时不随方程和时空的不同区域发生变化。
这样就有一些潜在的问题,比如低阶差分近似一般会带来大的耗散,即
高阶差分耗散小,但又会引入大的色散。一个小的数值涨落,随时间的演化不是消失,而是逐渐增大,使得演化发散。
近代计算流体力学发展了各种各样的有限差分和有限体积法,比如 FCT, Godunov, TVD, NND,ENO, WENO, COMPACT 算法等等,都是为了解决低阶与高阶,耗散与振荡的矛盾。
ENO 和 WENO 算法会根据局部的曲率,从一系列预先定义好的差分形式中选择最适合的离散核
对空间的不同区域使用不同的差分格式非常合理,比如说在一个激波的内部和外部,应该使用不同精度的差分近似及差分系数。
机器学习和数据驱动的方法如下:首先生成高分辨率的训练数据,然后从数据中学习微分的离散近似。产生高分辨率的训练数据可能花费很高,但是如果在小的系统生成解在流形空间的局域近似,然后应用于大的系统求解,可能会显著减少计算时间。
在有限积分格式下,Burgers 方程完全受每个cell边界上流入,流出的场量决定。所以唯一的挑战是根据cell的平均值精确的估计边界上的流(Flux)。这一步由神经网络给出。
计算分成3个步骤:
- 使用神经网络构造Cell边界上的空间微分,(利用边界两边Cell的场量均值)。
- 使用计算得到的空间微分去计算 Flux J。
- 使用旧的 Cell 均值减去左右边界上向外的 Flux J 来计算 Cell 均值的时间微分。并将时间微分(而非空间微分)的预测误差作为loss function进行优化。
作者尝试过使用传统的单调算法(此处单调指的是没有色散引起的振荡),比如 Godunov Flux,没有带来比神经网络模型更好的提升。
这篇文章提出本方法的缺陷是:(1)速度比普通差分近似慢很多。普通差分的卷积核一般用到左右5个格子,而本方法神经网络参数约几千个。(2)本文方法是在规则格点上的差分方案,如何推广到不规则格点呢?图神经网络与点云神经网络显然是很好的候选。这个需要进一步的研究。
展望
如果神经网络能够根据偏微分方程,边界条件和初始条件生成不规则的离散化格子,在曲率大的区域构造更精细的格子,在平坦区域构造粗粒度格子,并在不规则格子上构建最优的差分离散化方案,可能会带来计算流体力学的新突破。
代码:
旧版 https://github.com/google/data-driven-discretization-1d
新版 https://github.com/google-research/data-driven-pdes
新版开源代码中有 Tutorial 和 Example