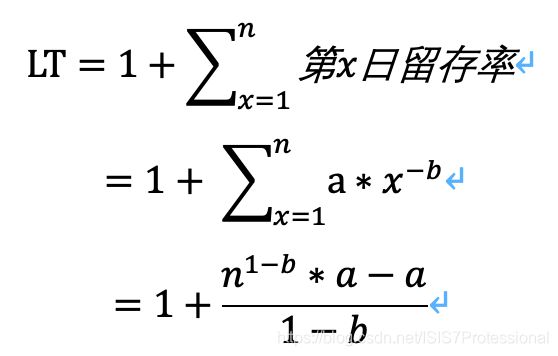APP的LT预估模型及LTV/ROI计算

LT ( Life Time ) 生命周期（日）。

LTV ( Life Time Value ) 用户生命周期的总价值。

CAC ( Customer Acquisition Cost ) 用户获取成本。 

ROI ( Return on investment ) 投资回报率。ROI = LTV/CAC。

    一般来说，当一款APP的ROI小于1时，说明该产品处于亏损状态；当一款APP的ROI大于1时，说明该产品处于盈利状态。而在盈利状态下，可考虑加大推广吸纳更多用户。那么该如何验证ROI是否大于1，又该如何进行下一步推广呢？

一、如何验证ROI是否大于1

1.1 回报周期

    小熙开了一家花店，投入10万元，一年后收入10万元。

    小爱也开了一家花店，同样投入10万元，3个月后收入10万元。

    两人的花店ROI大于1吗？是否可以继续开分店？

    从现有数据看，小熙和小爱在第二年都是盈利的，ROI均大于1。而显然小爱在3个月时ROI便大于1了。这里小熙的回报周期是1年，小爱的回报周期是3个月。回报周期越短，相应的风险也就越低。

    回到一款APP，不同行业的回报周期不同。我们可以根据现有的回报周期以及期望的回报周期来优化产品，使得在可接受的时间段内拿到一个大于1的ROI。（现有回报周期计算见1.2）

1.2 生命周期LT

    300元(CAC)买来一个用户，用户每活跃一天可带来5元收益(ARPU)，该用户一年内(期望回报周期)活跃了100天(LT)，总收益为500元(LTV=LT*ARPU)，ROI=LTV/CAC=1.67。

    CAC 300元 可根据 “支出/新用户数”获取，ARPU 5元 可根据“收入/活跃用户数”估算(忽略单用户生命周期内arpu的变动)，LT 100天又该如何得到？

LT预估模型：

    x为留存天数，y为对应天数的留存率，a为留存系数，b为衰减系数。

    通俗解释为 1+后续每天留存率。

    后续每天的留存率是一条衰减曲线，可以用幂函数y=a*x^(-b)拟合，对幂函数求积分获取曲线下方的面积，即为上述公式。

    n为期望回报周期，可根据需要选180天、365天、730天等。

    使得ROI=1的n便是现有回报周期。

 

具体计算参考：

EXCEL公式获取幂函数系数解析​​​​​​​

python获取留存曲线的幂函数系数并计算生命周期LT

幂函数衰减系数公式推导（最小二乘法求解一元线性回归方程系数） 

二、如何进行下一步推广

    当期望回报周期内roi>1时，为了进一步推广app，通常会挖掘新渠道或加大现有渠道买量。此时，我们可模拟渠道roi来计算单一渠道的回报周期、衡量每个渠道的质量，对增加购买哪个渠道进行决策支持。

    当然，ROI公式不变，只需将每个指标调整为各渠道数据即可。

    ROI = LTV / CAC = (LT*ARPU) / (COST/DNU)

三、（补充）数据可用性及时效性问题

    进行LT预测时，已知留存越多，拟合曲线的误差可能越小。比如，采用1~30天留存率拟合效果优于1~7天留存率拟合效果（可用R方评估）。而想要高拟合度，就意味着需要拉长渠道评估周期，评估周期太长又会面临成本和评估结果时效性问题（30天前优质渠道如今是否依旧优质）。可根据实际情况平衡两者关系。

相关推荐： 

数据埋点知识备份 https://blog.csdn.net/ISIS7Protessional/article/details/121491694

数据仓库知识备份https://blog.csdn.net/ISIS7Protessional/article/details/123093082

AB实验知识备份https://blog.csdn.net/ISIS7Protessional/article/details/123139221