机器学习入门:逻辑回归-2
机器学习入门:逻辑回归
1、实验描述
-
本实验主要内容是,通过使用pandas对鸢尾花数据集进预处理,根据预处理数据建立logistics regression
模型,并训练模型,再利用训练出来的模型做预测,并最终使用图形的方式展示预测结果。 -
实验时长:45分钟
-
主要步骤:
-
加载iris数据集
-
读取对应的标签和特征
-
将标签值从string映射整数型
-
对特征做标准化和映射多项式特征集
-
模型创建
-
模型的预测
-
模型评估
-
结果展示
-
2、实验环境
- 虚拟机数量:1
- 系统版本:CentOS 7.5
- scikit-learn版本: 0.19.2
- pandas版本:0.22.4
- numpy版本:1.15.1
- matplotlib版本:2.2.3
- python版本:3.5
- IPython版本:6.5.0
3、相关技能
-
Python编程
-
Sklearn常见库的使用
-
数据预处理
-
逻辑回归建模
-
Matplotlib画图
4、相关知识点
-
Pandas 读取文件
-
Pandas读取特征、标签数据
-
使用pandas的Categorical 映射标签值
-
使用Pipeline串联模型流程
-
逻辑回归模型的建立
-
模型预测
-
模型评估
5、实现效果
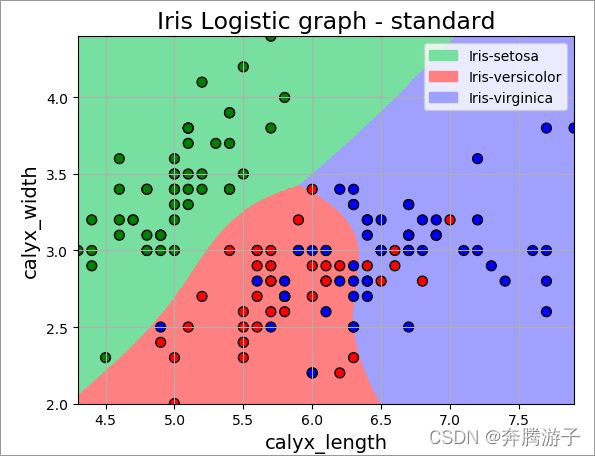
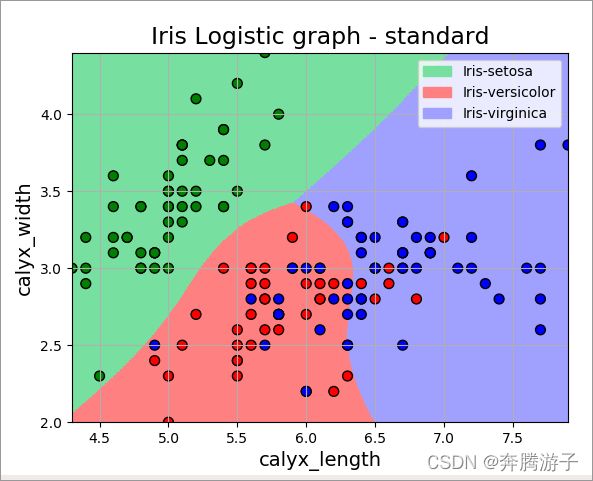
- 利用逻辑回归完成对鸢尾花多分类最终效果如下图:
6、实验步骤
6.1进入Anaconda创建的虚拟环境“ML”
6.1.1从实验数据公共目录将实验数据文件iris.data拷贝到zkpk的家目录下
[zkpk@master ~]$ cd
[zkpk@master ~]$ cp /home/zkpk/experiment/iris.data /home/zkpk/
6.1.2数据集介绍:数据集信息:“iris.data”。该数据集共包括150行,每行为1个样本。每个样本有5个字段,分别是:花萼长度(单位cm)、花萼宽度(单位:cm)、花瓣长度(单位:cm)、花瓣宽度(单位:cm)、类别(共3类,分别是:Iris Setosa、Iris Versicolour、Iris Virginica)
6.1.3在zkpk的家目录下执行如下命令
[zkpk@master ~]$ cd
[zkpk@master ~]$ source activate ML
(ML) [zkpk@ master ML]$
6.1.4此时已经进入虚拟环境。键入如下命令,进入ipython交互是编程环境
(ML) [zkpk@ master ML]$ ipython
Python 3.5.4 |Anaconda, Inc.| (default, Nov 3 2017, 20:01:27)
Type 'copyright', 'credits' or 'license' for more information
IPython 6.2.1 -- An enhanced Interactive Python. Type '?' for help.
In [1]:
6.2在Ipython交互式编程环境中开始进行实验
6.2.1导入实验所需的包
In [1]: import pandas as pd
...: import matplotlib.pyplot as plt
...: import numpy as np
...: from sklearn.preprocessing import StandardScaler, PolynomialFeatures # StandardScaler 将特征正则化;PolynomialFeatures 用于生成多项式的、互动的特征数据
...: from sklearn.linear_model import LogisticRegression
...: from sklearn.pipeline import Pipeline
...: import matplotlib as mpl
...: import matplotlib.patches as mpatches
...:
6.2.2读取数据文件
In [2]: path = 'iris.data'
In [3]: data = pd.read_csv(path)
6.2.3读取对应的维度数据,分别作为特征值x, 和标签值y
In [11]: x = data.values[:, :-1] # 对应数据集中的前4列
...: y = data.values[:,-1] # 对应第5列
6.2.4打印对应的特征值和标签值的shape
In [12]: print("x's shape", x.shape)
...: print("y's shape", y.shape)
...:
6.2.5使用pandas的Categorical方法将标签值从String映射成Int。并打印对应的类别值.
In [16]: y = pd.Categorical(y).codes # Categorical()计算列表型数据中的类别;codes将类别信息转化成数值信息
...: np.unique(y)
...:
6.2.6实验中选择前两列作为特征值(分别是花萼长度和宽度)
In [17]: x = x[:,:2]
6.2.7使用sklearn自带的Pipeline将数据预处理和构建模型串起来,连着做。
In [20]: lr = Pipeline([('sc', StandardScaler()), ('poly',PolynomialFeatures(degree=3)), ('clf', LogisticRegression())]) # StandardScaler()标准化处理;PolynomialFeatures映射到n维多项式特征集, degree参数用来控制多项式的度;LogisticRegression()逻辑回归模型
In [21]:
6.2.8使用数据进行模型训练
In [21]: model = lr.fit(x, y)
...:
6.2.9使用创建的模型进行预测
In [22]: y_pred = model.predict(x)
6.2.10设置输出的精度
In [24]: np.set_printoptions(suppress=True) # 设置输出的精度, suppress是否压缩由科学计数法表示的浮点数
6.3评测模型的效果
In [27]: print(u'准确度: %2.f%%' %(100* np.mean(y_pred == y)))
6.4根据预测值和标签值绘制逻辑回归模型对鸢尾花数据集三分类的实验效果;具体步骤及说明见下边代码、注释。
In [28]: N, M = 500, 500 # 横纵各采样500个值
...: x1_min, x1_max = x[:, 0].min(), x[:, 0].max() # 第0列的范围
...: x2_min, x2_max = x[:, 1].min(), x[:, 1].max() # 第1列的范围
...: t1 = np.linspace(x1_min, x1_max, N) # linspace()生成等间隔数列;x1_min作为数列的开头;x1_max作为结尾,N作为数列元素的个数
...: t2 = np.linspace(x2_min, x2_max, M)
...:
...: x1, x2 = np.meshgrid(t1, t2) # 生成网格坐标点
...: x_test = np.stack((x1.flat, x2.flat), axis=1) # 测试点;flat方法,返回数组的flatiter迭代器;
...:
...: cm_light = mpl.colors.ListedColormap(['#77E0A0', '#FF8080', '#A0A0FF'])
...: cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
...:
...: y_hat = model.predict(x_test) # 预测值
...: y_hat = y_hat.reshape(x1.shape) # 使之与输入的形状相同
...:
...: plt.figure(facecolor='w') #可设置控制dpi、边界颜色、图形大小、和子区( subplot)
...: plt.pcolormesh(x1, x2, y_hat, cmap=cm_light) # 预测值的分类显示
...: plt.scatter(x[:, 0], x[:, 1], c=y, edgecolors='k', s=50, cmap=cm_dark) # 样本的显示
...: plt.xlabel(u'calyx_length', fontsize=14)
...: plt.ylabel(u'calyx_width', fontsize=14)
...:
...: # 来调整x,y坐标范围
...: plt.xlim(x1_min, x1_max)
...: plt.ylim(x2_min, x2_max)
...: plt.grid()
...:
...: ### 不同类的区域显示不同的颜色,自定义字典将实例或类型映射到图例
...: patchs = [mpatches.Patch(color='#77E0A0', label='Iris-setosa'),
...: mpatches.Patch(color='#FF8080', label='Iris-versicolor'),
...: mpatches.Patch(color='#A0A0FF', label='Iris-virginica')]
...:
...: # 设置图例和其中的文本的显示
...: plt.legend(handles=patchs, fancybox=True, framealpha=0.8)
...: plt.title(u'Iris Logistic graph - standard', fontsize=17)
...: plt.show()
...:
7、总结
完成本次实验,可以基本掌握关于逻辑回归建立模型的相关知识。在实验中我们对数据进行了标准化和多项式特征映射处理,最终通过逻辑回归模型完成多分类任务,最终将结果展示出来。