十大机器学习算法(一)
参加建模已经两次了。浑浑噩噩的看了一些书和视频,但是被人问到十大机器学习算法的时候竟然蒙了。差了一下才发现一部分算法都是熟面孔,然后写这篇文章来记录整理一下十大机器学习算法的学习笔记。笔记内容将包括基本理论和算法实现,每篇两到三个算法。
##参考书籍《数学建模算法与应用》--司守奎、孙兆亮 [1]
##Python代码参考-邱锡鹏神经网络与深度学习 [2]
##部分图片参考知乎文章Machine Learning: 十大机器学习算法 - 知乎 (zhihu.com) [3]
基本的机器算法如下:
- 线性回归算法 Linear Regression
- 支持向量机算法 (Support Vector Machine,SVM)
- 最近邻居/k-近邻算法 (K-Nearest Neighbors,KNN)
- 逻辑回归算法 Logistic Regression
- 决策树算法 Decision Tree
- k-平均算法 K-Means
- 随机森林算法 Random Forest
- 朴素贝叶斯算法 Naive Bayes
- 降维算法 Dimensional Reduction
- 梯度增强算法 Gradient Boosting
一、线性回归
1.基本原理
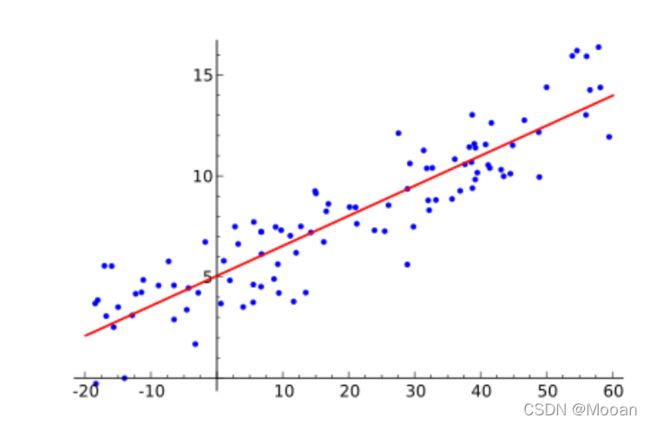
从二维坐标系来看,就是从一堆点里拟合出一条线性方程(如下图,图源[3]),但当X表示为一个m维的向量,那么回归方程也可以表示为一个m维空间中的直线。应用实际解决问题时,常把不同的自变量作为不同的维度,线性拟合自变量同因变量之间的线性关系。
2.求解过程
(1)回归模型的假设检验:(对自变量的相关性分析)
假设自变量与因变量相关->F检验拒绝假设或接受假设
(2)线性回归和检验
循环![]() ,通过损失函数——最小二乘法计算损失,通过优化函数——梯度下降确定损失最低点时的
,通过损失函数——最小二乘法计算损失,通过优化函数——梯度下降确定损失最低点时的![]() ,退出循环。
,退出循环。
通过![]() 检验拟合程度。
检验拟合程度。
以下是[2]通过torch搭建的logistics模型,代码的搭建过程就是模型的训练过程
%matplotlib inline
import torch
from IPython import display
import matplotlib.pyplot as plt
import numpy as np
import random
# 1生成数据集
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4] # 样本真实权重
true_b = 4.2 # 样本真实偏差
features = torch.randn(num_examples, num_inputs,
dtype=torch.float32)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
dtype=torch.float32)
# np.random.normal() 从正态分布中抽取随机样本
# labels加上一个随机噪声
# 2读取数据
# data_iter(batch_size, features, labels)
# 每次返回batch_size个随机样本的特征和标签
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # 样本的读取顺序是随机的,indices是一个打乱的下标序列
for i in range(0, num_examples, batch_size):
j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # 最后一次可能不足一个batch
yield features.index_select(0, j), labels.index_select(0, j) # LongTensor是int64
# 3参数初始化
# 我们将权初始化成均值为0、标准差为0.01的正态随机数,偏差则初始化成0
# 也就是我们要迭代更新的参数
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)
# inplace版本
# 之后模型训练中,需要对这些参数求梯度来迭代参数的值,所以requires_grad=True
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
# 定义模型
def linreg(X, w, b):
return torch.mm(X, w) + b
#定义损失函数
def squared_loss(y_hat, y):
return (y_hat - y.view(y_hat.size())) ** 2 / 2
#定义优化函数 sgd([w, b], 学习率, 批量大小)
def sgd(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data
# 训练模型
lr = 0.03 # 学习率
num_epochs = 3 # 迭代周期个数,一个迭代周期中将遍历所有样本
net = linreg # 简化了函数的名称
loss = squared_loss
for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
# 在每一个迭代周期中,会使用训练数据集中所有样本一次(假设样本数能够被批量大小整除)。X
# 和y分别是小批量样本的特征和标签
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y).sum() # l是有关小批量X和y的损失
l.backward() # 小批量的损失对模型参数求梯度
sgd([w, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数[w, b]
# 一般在反向传播之前把梯度清零
w.grad.data.zero_()
b.grad.data.zero_()
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
# 比较学到的参数和生成训练集的参数,很接近。
print(true_w, '\n', w)
print(true_b, '\n', b)3.算法实现
(1)如果不用作图,而且没有太高的要求,推荐使用SPSS。我习惯用这个,无敌方便。
(2)Python sklearn库可以非常方便的调用logistics回归模型,不用再写这么长的代码自己定义模型了。
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
diabetes = datasets.load_diabetes()
diabetes_X = diabetes.data[:,np.newaxis,2]
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]
regr = linear_model.LinearRegression()
regr.fit(diabetes_X_train, diabetes_y_train) #这里就是在训练模型了
print('Coefficients: \n', regr.coef_) #这就是w0,常数项
print("Residual sum of squares: %.2f" % np.mean((regr.predict(diabetes_X_test) - diabetes_y_test) ** 2)) #这个是预测与真实的差
print('Variance score: %.2f' % regr.score(diabetes_X_test, diabetes_y_test)) #这里就是得分,1为拟合最好,0最差
plt.scatter(diabetes_X_test, diabetes_y_test, color = 'black')
plt.plot(diabetes_X_test,regr.predict(diabetes_X_test), color='blue',linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()上述代码参照以下链接:
(1条消息) scikit-learn 学习笔记(一)_Zhang_Yu_Joseph的博客-CSDN博客
这个博主把线性回归写的很详细,而且不只是使用最基础的损失函数,有多种方法对比。一起学习一下吧。
(3)MATLAB、R语言等。
regress (Y,X,alpha) %MATLAB代码 alpha为置信度4.注意
线性回归中的“线性”指的是回归方程中系数![]() 是线性的,如果方程中含有
是线性的,如果方程中含有![]() 这种(你觉得多次非线性的项),可以将
这种(你觉得多次非线性的项),可以将![]() 看成是
看成是![]() 即多一个维度,拟合的依然是线性方程。
即多一个维度,拟合的依然是线性方程。![]() 等项类似。
等项类似。
二、支持向量机算法
1.基本原理
简而言之,就是一个二分类的算法。其主要思想是找到一个超平面,使得他能够尽可能多的将两类数据点正确的分开,同时时两类数据点距离分类面最远。
2.求解过程
支持向量机主要分为三种:线性可分支持向量机、线性支持向量机、可分支持向量机。从字面意思就可以看出来线性指的是超平面线性(二维情况下可以理解为直线);可分指的是两类点完全分开。可以根据不同的需求使用不同的支持向量机。
主要步骤有:构造训练集、验证集和测试集->构造分类函数
##构造分类函数的过程中用到了二次规划问题,详细可以看书,但是代码中没有体现()。
3.算法实现
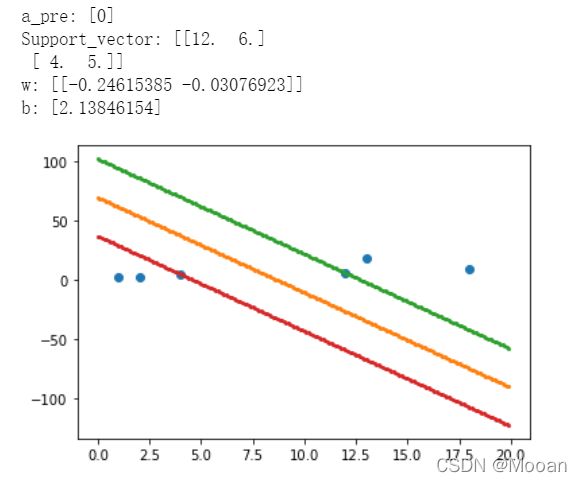
(1)Python-(结果并没有达到两类点最远,原因正在学习中...)
import numpy as np
import joblib
from sklearn import svm
import matplotlib.pyplot as plt
x = [[1, 2], [4, 5], [18, 9], [12, 6], [2, 3], [13, 18]]
x = np.array(x)
y = [1, 1, 0, 0, 1, 0]
y = np.array(y)
# 训练模型
model = svm.SVC(C=10, kernel='linear')
model.fit(x, y)
# 预测
a = [[8, 6]]
a_pre = model.predict(a)
print("a_pre:", a_pre)
# 对应的支持向量
Support_vector = model.support_vectors_
print("Support_vector:", Support_vector)
# 线性分类对应的参数
w = model.coef_
print("w:", w)
b = model.intercept_
print("b:", b)
# 训练集散点图
plt.scatter(x[:, 0], x[:, 1])
if w[0, 1] != 0:
xx = np.arange(0, 20, 0.1)
# 最佳分类线
yy = -w[0, 0]/w[0, 1] * xx - b/w[0, 1]
plt.scatter(xx, yy, s=4)
# 支持向量
b1 = Support_vector[0, 1] + w[0, 0]/w[0, 1] * Support_vector[0, 0]
b2 = Support_vector[1, 1] + w[0, 0]/w[0, 1] * Support_vector[1, 0]
yy1 = -w[0, 0] / w[0, 1] * xx + b1
plt.scatter(xx, yy1, s=4)
yy2 = -w[0, 0] / w[0, 1] * xx + b2
plt.scatter(xx, yy2, s=4)
else:
xx = np.ones(100) * (-b) / w[0, 0]
yy = np.arange(0, 10, 0.1)
plt.scatter(xx, yy)
plt.show()结果图片
重点关注学习svm.SVC()函数中的参数
model = svm.SVC(C=2.0,
kernel='rbf',
degree=3,
gamma='auto',
coef0=0.0,
shrinking=True,
probability=False,
tol=0.001,
cache_size=200,
class_weight=None,
verbose=False,
max_iter=-1,
decision_function_shape=None,
random_state=None)C:SVC的惩罚参数,默认值是1.0;C越大,对误分类的惩罚增大,趋向于对训练集完全分对的情况,这样对训练集测试时准确率很高,但泛化能力弱。C值小,对误分类的惩罚减小,允许容错,将他们当成噪声点,泛化能力较强。
kernel :核函数,默认是rbf,可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ linear:线性分类器(C越大分类效果越好,但有可能会过拟合(default C=1)) Python机器学习笔记:SVM(2)——SVM核函数 - 知乎
degree :多项式poly函数的维度,默认是3,选择其他核函数时会被忽略。
gamma : ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’。 如果gamma是’auto’,那么实际系数是1 / n_features。
coef0 :核函数中的独立项。 它只在’poly’和’sigmoid’中很重要。
probability :是否启用概率估计。 必须在调用fit之前启用它,并且会减慢该方法的速度。默认为False
shrinking :是否采用shrinking heuristic方法(收缩启发式),默认为true
tol :停止训练的误差值大小,默认为1e-3
cache_size :核函数cache缓存大小,默认为200
class_weight :类别的权重,字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)
verbose :允许冗余输出
max_iter :最大迭代次数。-1为无限制。
decision_function_shape :‘ovo’, ‘ovr’ or None, default=ovr
关于‘ovo’, ‘ovr’的解释: 一对多法(one-versus-rest,简称OVR SVMs):训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类,这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类。 一对一法(one-versus-one,简称OVO SVMs或者pairwise):其做法是在任意两类样本之间设计一个SVM,因此k个类别的样本就需要设计k(k-1)/2个SVM。当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别。 详细讲解,可以参考这篇博客:SVM多分类的两种方式_xfChen2的博客-CSDN博客_svm多分类
random_state :数据洗牌时的种子值,int值,default=None 在随机数据混洗时使用的伪随机数生成器的种子。 如果是int,则random_state是随机数生成器使用的种子; 如果是RandomState实例,则random_state是随机数生成器; 如果为None,则随机数生成器是np.random使用的RandomState实例。
个人认为最重要的参数有:C、kernel、degree、gamma、coef0、decision_function_shape。
##以上内容来自[2]
(2)MATLAB
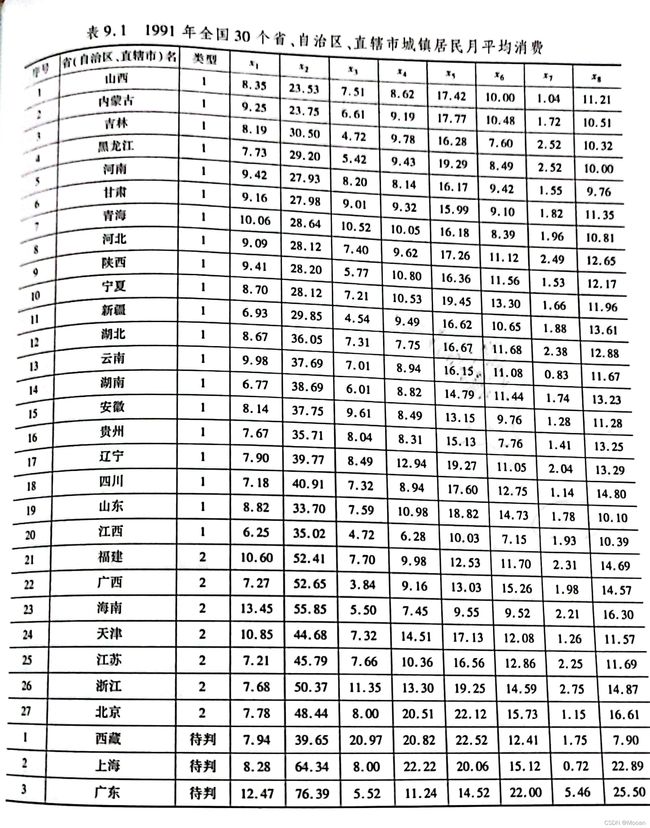
例题+代码 ##来源[1]
clc,clear
a0=load('fenlei.txt'); %把表中数据保存在文件fenlei.txt中
a=a0';b0=a(:,[1:27]);dd0=a(:,[28:end]);
[b,ps]=mapstd(b0); %已分类的数据标准化
dd=mapstd('apply',dd0,ps); %未分类的数据标准化
group=[ones(20,1);2*ones(7,1)]; %已知样本点的类别标号
s=fitcsvm(b',group) %训练支持向量机分类器
sv_index=s.SupportVectorIndices %返回支持向量的标号
beta=s.Alpha %返回分类函数的权系数
bb=s.Bias %返回分类函数的常数项
mean_and_std_trans=s.ScaleData %第一行返回的是已知样本点均值向量的相反数,第二行返回的是标准差向量的倒数
check=predict(s,b') %验证已知样本点
err_rate=1-sum(group==check)/length(group) %计算已知样本点的误判率
solution=predict(s,dd') %对待判样本点进行分类注意:使用MATLAB代码需要下载最新的libsvm包。(新包下载的坑我已经踩了,详见我的上一篇文章)
代码跑出来了一串东西,我们只取结果,待测的分类应该是112.