【线性代数】4-2:投影(Porjections)
原文地址1:https://www.face2ai.com/Math-Linear-Algebra-Chapter-4-2转载请标明出处
Abstract: 本篇主要介绍的就是向量的映射,以映射到直线为引导,重点在于映射到子空间。
Keywords: Projections,Projection Onto a Subspace
投影
映射,投影,感觉怎么翻译都不太对,总能想到函数,不过好像在这部分,投影矩阵和函数的功能非常类似。在典型的三维正交基向量空间内,一个向量的投影到一个平面上一般是下面这种形式:

向量b投影到xy平面,和b投影到z轴的一种几何上的反应,当然超过三维,就没办法画出来的,但是原理都一样,通过垂直(正交),将不在子空间的向量转换到子空间内最接近原始向量 b ⃗ \vec{b} b 的投影向量 b ⃗ ^ \hat{\vec{b}} b^来近似原始向量,这种方法在最小二乘法中得到了完美的应用,以及后面将要做的一些分解,上一篇提到的split(分解到子空间的split),都可以利用projection的原理。
继续解读上图,向量被分级到了正交的两个子空间,xy平面,和z轴,这两个子空间互为orthogonal complements,并且满足下面两种关系:
p 1 ⃗ + p 2 ⃗ = b ⃗ P 1 + P 2 = I \vec{p_1}+\vec{p_2}=\vec{b}\\ P_1+P_2=I p1+p2=bP1+P2=I
第一个式子就是个典型的split,比如物理里面力的分解,速度分解,都是把向量分解到你想要的方向,然后我们把向量分解到orthogonal complements的子空间中,就得到了我们想要的projection
第二个式子是projection matrix之间的关系,这里可以轻易的看出来,映射到xy平面 P 1 = [ 1 0 0 0 1 0 0 0 0 ] P_1=\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix} P1=⎣⎡100010000⎦⎤,同理到z轴的就是 P 2 = [ 0 0 0 0 0 0 0 0 1 ] P_2=\begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix} P2=⎣⎡000000001⎦⎤,可以看出 P 1 + P 2 = I P_1+P_2=I P1+P2=I
。
映射到直线
点乘映射
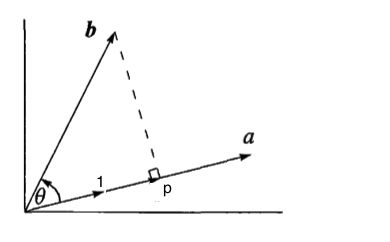
把一个向量 b ⃗ \vec{b} b 映射到一条直线 a a a,等价于问题类似于把一个向量projection到另一个向量上,这个和我们之前学习的dot product有点像,如果
w h e n ∣ i ⃗ ∣ = 1 b ⃗ ⋅ i ⃗ = ∣ b ⃗ ∣ ∣ i ⃗ ∣ c o s ( θ ) = ∣ b ⃗ ∣ c o s ( θ ) when\,|\vec{i}|=1\\ \vec{b} \cdot \vec{i}=|\vec{b}||\vec{i}|cos(\theta)=|\vec{b}|cos(\theta) when∣i∣=1b⋅i=∣b∣∣i∣cos(θ)=∣b∣cos(θ)
其中夹角就是下图中 θ \theta θ
可以看到映射到向量a上等价于和a方向上的单位向量dot product,假设 p ⃗ \vec{p} p 是 b ⃗ \vec{b} b 的投影结果,那么 i ⃗ = a ⃗ ∣ a ⃗ ∣ \vec{i}=\frac{\vec{a}}{|\vec{a}|} i=∣a∣a
∣ p ⃗ ∣ = ∣ b ⃗ ∣ c o s ( θ ) = b ⃗ ⋅ i ⃗ = b ⃗ ⋅ a ⃗ ∣ a ⃗ ∣ p ⃗ = ∣ p ⃗ ∣ i ⃗ = ∣ p ⃗ ∣ a ⃗ ∣ a ⃗ ∣ s o : p ⃗ = b ⃗ ⋅ a ⃗ ∣ a ⃗ ∣ ∣ a ⃗ ∣ a ⃗ |\vec{p}|=|\vec{b}|cos(\theta)=\vec{b} \cdot \vec{i}=\vec{b} \cdot \frac{\vec{a}}{|\vec{a}|}\\ \vec{p}=|\vec{p}|\vec{i}=|\vec{p}|\frac{\vec{a}}{|\vec{a}|}\\ so:\\ \vec{p}=\frac{\vec{b}\cdot\vec{a}}{|\vec{a}||\vec{a}|}\vec{a} ∣p∣=∣b∣cos(θ)=b⋅i=b⋅∣a∣ap=∣p∣i=∣p∣∣a∣aso:p=∣a∣∣a∣b⋅aa
把向量中的dot product都换成转置相乘的模式就得到了
p ⃗ = b ⃗ T a ⃗ a ⃗ T a ⃗ a ⃗ \vec{p}=\frac{\vec{b}^T\vec{a}}{\vec{a}^T \vec{a}}\vec{a} p=aTabTaa
没错,跟书上的推到方式不太一样,但是,从另一个角度得出了正确结论,其实这段不算困难,只是符号和向量长度的问题,但是由于在草稿纸上没写清楚,刚才有不得不重新推到了一边跟书上不一样是因为系数转置的原因,除法最后得出的是个数字,所以把它转置不影响结果:
p ⃗ = ( b ⃗ T a ⃗ a ⃗ T a ⃗ ) T a ⃗ = a ⃗ T b ⃗ a ⃗ T a ⃗ a ⃗ \vec{p}=(\frac{\vec{b}^T\vec{a}}{\vec{a}^T \vec{a}})^T\vec{a}=\frac{\vec{a}^T\vec{b}}{\vec{a}^T \vec{a}}\vec{a} p=(aTabTa)Ta=aTaaTba
这样就得出了和书上一样的结论,书上是通过正交得出的结论,在介绍书上的办法之前要说一个我刚发现的很基础的东西,就是向量连续乘法和矩阵(非向量矩阵)连续乘法不一样,矩阵连续乘法可以结合,向量不可以,比如我们用矩阵规模来解释一下
A B C : ( 2 × 3 ) ( 3 × 4 ) ( 4 × 5 ) = ( 2 × 5 ) ( A B ) C = A ( B C ) ABC:(2 \times 3)(3 \times 4)(4 \times 5)=(2 \times 5)\\ (AB)C=A(BC)\\ ABC:(2×3)(3×4)(4×5)=(2×5)(AB)C=A(BC)
但是对于向量:
a ⃗ T b ⃗ c ⃗ : ( 1 × n ) ( n × 1 ) ( x × y ) = ( x × y ) \vec{a}^T \vec{b}\vec{c}:(1 \times n)(n \times 1)(x \times y)=(x \times y) aTbc:(1×n)(n×1)(x×y)=(x×y)
不可以结合,因为尺寸不满足需求,上面的变形中间就有这个问题,所以向量乘法结合律最好别用,用的话也自己搞好大家的尺寸,别最后对不上。
和投影正交
不错这个才是正统书上的方法,推到相对上面还要简单一些主要用到了一个向量的差与投影结果 p ⃗ \vec{p} p垂直这一关系,具体贴上原书两张图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-29J8E7ad-1592544186792)(https://tony4ai-1251394096.cos.ap-hongkong.myqcloud.com/blog_images/Math-Linear-Algebra-Chapter-4-2/projection_2.png)]
还是将 b ⃗ \vec{b} b 投影到 a ⃗ \vec{a} a ,假设得到的投影是 x ^ a ⃗ \hat{x}\vec{a} x^a ;可以得到一个差向量 e ⃗ \vec{e} e (这个向量其实就是后面最小二乘法的误差,error的缩写)有些时候我们必须把向量近似到一个空间,以方便进一步计算,这时候希望得到误差最小的近似,误差就是这个 e ⃗ \vec{e} e 的模长,并且这个 e ⃗ \vec{e} e 和 a ⃗ \vec{a} a 是垂直关系,也就是正交,那么就有了 a ⃗ T ( b ⃗ − x ^ a ⃗ ) \vec{a}^T(\vec{b}-\hat{x}\vec{a}) aT(b−x^a)=0,最后能求出投影长度 x ^ \hat{x} x^,
p ⃗ = x ^ a ⃗ = a ⃗ x ^ = a ⃗ a ⃗ T b ⃗ a ⃗ T a ⃗ \vec{p} =\hat{x}\vec{a}=\vec{a}\hat{x} =\vec{a}\frac{\vec{a}^T\vec{b}}{\vec{a}^T \vec{a}} p=x^a=ax^=aaTaaTb
下图就是详细的集合描述,大家不要过度依赖图片,因为有时候想象力更重要,因为一旦超过四维,图就没有了,只能靠想象和逻辑推导了。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gOWc4vhR-1592544186796)(https://tony4ai-1251394096.cos.ap-hongkong.myqcloud.com/blog_images/Math-Linear-Algebra-Chapter-4-2/projection_3.png)]
根据上面公式可以得出投影矩阵
p ⃗ = P b ⃗ = a ⃗ a ⃗ T a ⃗ T a ⃗ b ⃗ S o : P = a ⃗ a ⃗ T a ⃗ T a ⃗ \vec{p} =P\vec{b} =\frac{\vec{a}\vec{a}^T}{\vec{a}^T \vec{a}}\vec{b}\\ So:\\ P=\frac{\vec{a}\vec{a}^T}{\vec{a}^T \vec{a}} p=Pb=aTaaaTbSo:P=aTaaaT
这个投影矩阵是投影到向量a的,同理,其实可以投影到向量e所在的直线,因为 e ⃗ = b ⃗ − p ⃗ \vec{e}=\vec{b}-\vec{p} e=b−p 所以可以得出下面等式:
e ⃗ = b ⃗ − P b ⃗ = ( I − P ) b ⃗ \vec{e}=\vec{b}-P\vec{b}=(I-P)\vec{b} e=b−Pb=(I−P)b
那么这样的话, ( I − P ) (I-P) (I−P) 也是一个投影矩阵,投影到向量e所在直线的投影矩阵。
小结
如果 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b 在同一条直线上,那么可以得出 P b ⃗ = b ⃗ P\vec{b}=\vec{b} Pb=b;
如果 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b 垂直,那么 P b ⃗ = 0 P\vec{b}=0 Pb=0;
这里的投影矩阵相当于一个函数映射,把一个矩阵垂直的映射到另一个向量,这个投影矩阵就是我们非常关心,也具有很多有趣性质的矩阵 P
映射到子空间
上面说的映射到直线,用一个向量就能准确的描述出直线的方向,但是对于子空间,最好的描述方式就是basis,把basis作为列组合到一起,就是矩阵B,子空间就是B的列空间。这样更方便下面的计算,投影到子空间 C ( B ) C(B) C(B) ,这次试用书中映射到直线的类比方法,假设 a ⃗ \vec{a} a 向 C ( B ) C(B) C(B) 投影得到向量 p ⃗ = B x ^ \vec{p}=B\hat{x} p=Bx^ ,这样我们就可以得到 e ⃗ \vec{e} e 了,并且 e ⃗ \vec{e} e 正交于子空间 C ( B ) C(B) C(B) ,那么
e ⃗ = a ⃗ − B x ^ ( c o l ( B ) i ) T e ⃗ = 0 B T e ⃗ = 0 \vec{e}= \vec{a}-B\hat{x}\\ (col(B)_i)^T\vec{e}=0\\ B^T\vec{e}=0 e=a−Bx^(col(B)i)Te=0BTe=0
B的每一列都是一个basis,向量e和每一个basis都正交,也就是B的任一一列,故 B T e ⃗ = 0 B^T\vec{e}=0 BTe=0.
那么就可以按照上面直线的方法继续向下计算了
B T ( a − B x ^ ) = 0 p ⃗ = B x ^ = B B T B T B a ⃗ P = B B T B T B B^T(a-B\hat{x})=0\\ \vec{p}=B\hat{x}=\frac{BB^T}{B^TB}\vec{a}\\ P=\frac{BB^T}{B^TB} BT(a−Bx^)=0p=Bx^=BTBBBTaP=BTBBBT
思维过程和直线相似,就不在详细描述这里指的注意的是。
- subspace是B的列空间
- 向量e和列向量正交,根据上一篇的结论 e ⃗ = ( a ⃗ − B x ^ ) ∈ N ( B T ) \vec{e}=(\vec{a}-B\hat{x})\in N(B^T) e=(a−Bx^)∈N(BT) ,那么 B T ( a − B x ^ ) = 0 B^T(a-B\hat{x})=0 BT(a−Bx^)=0
- 这里面是涉及到了一个求逆过程 B T B B^TB BTB 的逆,存在且仅存在于当B的所有列线性独立
解释: B T B B^TB BTB 的逆,存在且仅存在于当B的所有列线性独立
证明,检查 B T B B^TB BTB 的nullspace
B T B x ⃗ = 0 B T ( B x ⃗ ) = 0 f o r : B T ≠ 0 s o : B x ⃗ = 0 B^TB\vec{x}=0\\ B^T(B\vec{x})=0\\ for: \, B^T\neq 0\\ so: \, B\vec{x}=0 BTBx=0BT(Bx)=0for:BT=0so:Bx=0
也就是说 B T B B^TB BTB 的Nullspace和 B B B 的 Nullspace是相同的,如果想可逆,那么nullspace必须只有0,所以B必须是线性独立的,证毕。
B T B B^TB BTB 得到的是个小的方矩阵(对称,可逆),如果是 B B T BB^T BBT 得到的是个大方阵,怎么搞的都不会可逆(但是依然对称),他的rank就B的rank。
另外P还有些小性质:
- P 2 = P P^2=P P2=P
- P n = P P^n=P Pn=P
- distance from a ⃗ \vec{a} a to subspace is e ⃗ \vec{e} e
总结
本来以为这篇会短点,结果还是这么长,可以得出很多有意思的结论也算有所值,今天到此为止,我们来热烈庆祝十九大顺利召开。。蛤蛤蛤。。