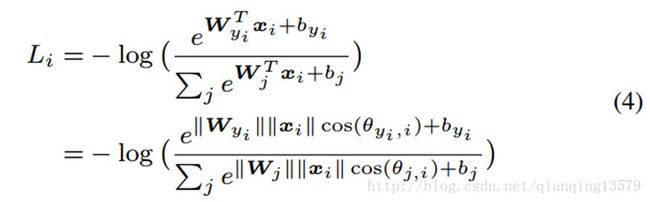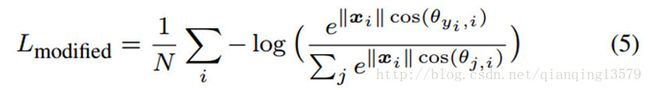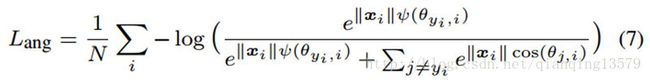SphereFace的翻译，解读以及训练

前段时间，由于工作需要，学习了一下论文《SphereFace: Deep Hypersphere Embedding for Face Recognition》,收获挺大的，这几天刚好有空，就整理了一下。博客分为三大部分，包括SphereFace的翻译，论文解读，以及模型的训练和测试。

---

目录

---

论文翻译

这里只翻译论文中最核心的第3章中的3.1,3.2和3.3

3.1 回顾Softmax loss

我们回顾一下softmax loss的决策准则。在二分类的情况下，softmax loss的后验概率为：

公式中 x x 就是学习到的特征向量，wi w i 和 bi b i 就是最后一个全连接层对应类别i的权值和偏置。如果 p1>p2 p 1 > p 2 ，预测的结果就是类别1，如果 p1<p2 p 1 < p 2 ,预测的结果就是类别2。从公式中很容易看出， WT1x+b1 W 1 T x + b 1 和 WT2x+b2 W 2 T x + b 2 决定了分类的结果。决策函数就是 (W1−W2)x+b1−b2=0 ( W 1 − W 2 ) x + b 1 − b 2 = 0 。 WTix+bi W i T x + b i 可以被写成 ||WTi||||x||cos(θi)+bi | | W i T | | | | x | | c o s ( θ i ) + b i ,其中 cos(θi) c o s ( θ i ) 就是 wi w i 和 x x 之间的夹角。如果我们归一化权重，并且将偏置设置为0，后验概率就变成了p1=||x||cos(θ1) p 1 = | | x | | c o s ( θ 1 ) 和 p2=||x||cos(θ2) p 2 = | | x | | c o s ( θ 2 ) 。注意p1和p2共享相同的x,最后的结果取决于角度 cos(θ1) c o s ( θ 1 ) 和 cos(θ2) c o s ( θ 2 ) 。决策函数就变成了 cos(θ1)−cos(θ2)=0 c o s ( θ 1 ) − c o s ( θ 2 ) = 0 。虽然上面的分析基于二分类，但是也适用于多分类。在训练的过程中，改进的softmaxloss( ||Wi||=1,bi=0 | | W i | | = 1 , b i = 0 )使得来自于同一类的样本特征具有更小的角度 θi θ i (即更大的cosine距离)。为了给改进后的softmax loss一个表达式，我们首先定义输入特征 xi x i 和他的label yi y i .原始的softmax loss可以写

成：

这里 fj f j 表示向量f的第j个元素(1<=j<=K,K就是类别数)，N就是训练样本的个数。在CNN中，f通常就是全连接层W的输出，所以， fj=WTjxi+bj f j = W j T x i + b j , fyi=WTyixi+byi f y i = W y i T x i + b y i ,这里 xi x i 是第i个训练样本， wj w j 表示w的第j列， wyi w y i 表示w的第 yi y i 列。我们可以进一步将公式3写成：

这里 θj,i(0<=θj,i<=π) θ j , i ( 0 <= θ j , i <= π ) 就是向量 wj w j 和 xi x i 之间的夹角。如上面分析，首先在每一次迭代中我们归一化权值 ||Wj|| | | W j | | 并且将偏置设置为0.然后我们可以将改进后的softmax loss写成：

虽然我们可以通过改进后基于角度的softmax loss学习特征，但是这些特征不一定就是可区分的。由于我们使用角度作为距离的矩阵，那么很自然的就可以将角度距离融合到学习到的特征来加强特征的可区分能力。本节最后，我们提出了一个新的方法来结合角度距离。

3.2 softmax loss中引进角度距离

我们没有设计一种新的loss函数，也没有构造一个softmax loss的加权组合(类似于对比loss),我们提出了一种更加自然的方法学习角度距离。从之前对softmax loss的分析来看，我们知道决策函数对特征分布的影响很大，所以我们的基本思想就是控制决策函数生成角度距离。我们首先使用二分类来解释一下我们的思路。

假设x是从类别1中学习到的特征， θi θ i 是 x x 和Wi W i 之间的角度，我们知道改进的softmax loss需要 cos(θ1)>cos(θ2) c o s ( θ 1 ) > c o s ( θ 2 ) 才能正确分类x。但是如果我们使用 cos(mθ1)>cos(θ2) c o s ( m θ 1 ) > c o s ( θ 2 ) (m是大于等于2的整数)来正确分类x会怎么样呢？有必要使得决策函数比以前更加严格，因为我们需要 cos(θ1) c o s ( θ 1 ) 比 cos(θ2) c o s ( θ 2 ) 更大。对于类别1来说 cos(mθ1)=cos(θ2) c o s ( m θ 1 ) = c o s ( θ 2 ) ，类似的，当 cos(mθ2)>cos(θ1) c o s ( m θ 2 ) > c o s ( θ 1 ) 的时候，该特征属于类别2，对于类别2来说，决策函数就是 cos(mθ2)=cos(θ1) c o s ( m θ 2 ) = c o s ( θ 1 ) ，假设所有的训练样本都被正确分类了，决策函数会生成一个 m−1m+1θ12 m − 1 m + 1 θ 2 1 的角度距离，这里的 θ12 θ 2 1 就是 W1 W 1 和 W2 W 2 的角度，从角度方面来看，当 θ1<θ2m θ 1 < θ 2 m 的时候，样本属于类别1，当 θ2<θ1m θ 2 < θ 1 m 的时候，样本属于类别1，两者都比原始的 θ1<θ2 θ 1 < θ 2 和 θ2<θ1 θ 2 < θ 1 更难，用公式来表示上面的思想就是：

其中 θyi,i θ y i , i 的范围是 [0,πm] [ 0 , π m ] 。为了消除该限制，并且使得在CNN中最优，我们通过一个角度函数 ψ(θyi,i) ψ ( θ y i , i ) 扩展 cos(θyi,i) c o s ( θ y i , i ) 的定义范围，这个函数在 [0,πm] [ 0 , π m ] 区间内等价于 cos(θyi,i) c o s ( θ y i , i ) 。我们提出的A-softmax loss可以表示为：

其中我们定义： ψ(θyi,i)=(−1)kcos(mθyi,i)−2k ψ ( θ y i , i ) = ( − 1 ) k c o s ( m θ y i , i ) − 2 k ， kπm<=θyi,i<=(k+1)πm,0<=k<=m−1 k π m <= θ y i , i <= ( k + 1 ) π m , 0 <= k <= m − 1 。m>=1是一个整数，用来控制角度距离的大小。当m=1,A-softmax loss变成了改进后的softmax loss.我们可以从决策函数角度来解释A-softmax loss.A-softmax loss对于不同的类别采用了不同的决策函数，每个决策函数比原始的更加严格，因此产生了角度距离。决策函数的比较见表1.

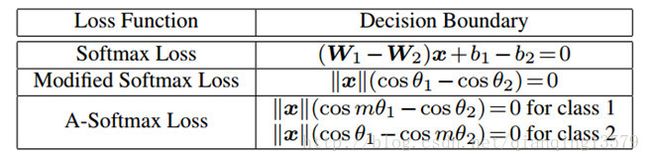
表1。 二分类中决策函数的比较。注意 θi θ i 就是 Wi W i 和 x x 之间的夹角.

从原始的softmax loss到改进的softmax loss,从优化内积到优化角度。从改进的softmax loss到A-softmax loss,让决策函数更加严格并且更加具有可区分性。当m增大，角度距离也会增加，当m=1的时候，角度距离为0。
通过A-softmax loss的监督，CNN学习到基于几何的角度距离的脸部特征。因为A-softmax loss需要wi=1,bi=0 w i = 1 , b i = 0 .预测仅仅依赖于样本x和wi之间的角度。所以，x可以以最小的角度被分类为某一类。添加参数m的目的是在不同人之间学习角度距离。为了便于梯度计算和反向传播，我们使用只包含 w w 和xi x i 的表达式替换了 cos(θj,i) c o s ( θ j , i ) 和 cos(mθyi,i) c o s ( m θ y i , i ) ，通过cosine和多角度公式的定义很容易做到这点。如果没有 θ θ ，我们能够计算x和w的导数，类似于softmax loss.

3.3 A-softmax loss的超球体解释

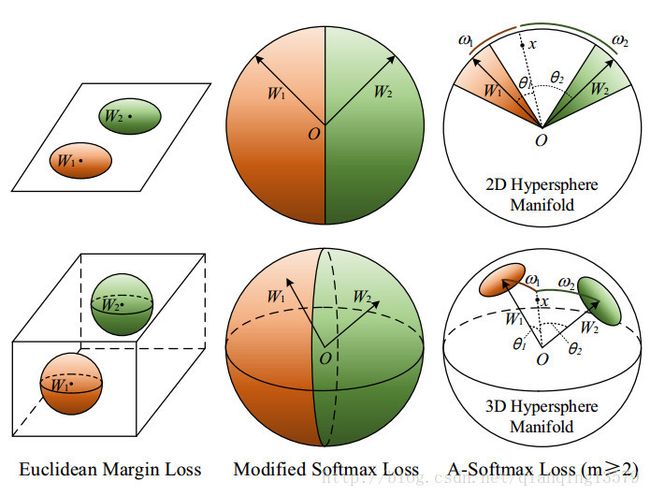
当m>=2的时候，对于正确分类来说A-softmax loss有更强的需求，这在不同类的特征之间产生了角度分类距离。A-softmax loss不仅使得学习到的特征更加可分，同样还具有更好的超球体解释。如图3所示

图3:欧式距离，改进的softmax loss和A-softmax loss的几何解释.第一行是2D特征约束，第二行是3D特征约束。橘黄色区域表示类别1的限制区间，绿色的表示类别2的限制区间。

A-softmax loss等价于在超球体空间学习特征，而欧式距离loss在欧式空间学习特征。简单起见，我们使用二分类来分析超球体解释。假设类别1的一个样本 x x 和两列权值W1 W 1 , W2 W 2 .A-softmax的分类的准则是 cos(mθ1)>cos(θ2) c o s ( m θ 1 ) > c o s ( θ 2 ) ，等价于 mθ1<θ2 m θ 1 < θ 2 ，注意到在单位球体
中， θ1，θ2 θ 1 ， θ 2 等价于他们对应的弧的长度 ω1,ω2 ω 1 , ω 2 。因为 ||W||1=||W||2=1 | | W | | 1 = | | W | | 2 = 1 ,决策依赖于弧的长度 ω1,ω2 ω 1 , ω 2 。决策函数等价于 mω1=ω2 m ω 1 = ω 2 ，x分类为类别1的区域为 mω1<ω2 m ω 1 < ω 2 。从几何角度来看，这是一个基于超球体空间的圆环区域。比如，在3D情况下，对应单位球体的一个圆环区域，如图3所示。注意，更大的m导致每类更小的圆环区域。为了更好的理解，图3提供了2D和3D的可视化图像。我们可以看到A-softmax loss在2D情况下使用了单位圆上的弧长约束，在3D情况下，使用了单位球体上的类圆区域约束。我们的分析表明A-softmax loss能够使得学习到的特征在超球体空间中更加可分。

---

论文解读

关于softmax loss的理解

阅读完这篇论文后，我对softmax loss有了更深的理解。

Softmax loss中的概率计算公式：

公式中 x x 就是学习到的特征向量，wi w i 和 bi b i 就是最后一个全连接层对应类别i的权值和偏置。

关于这个公式，借助CNN来理解一下。
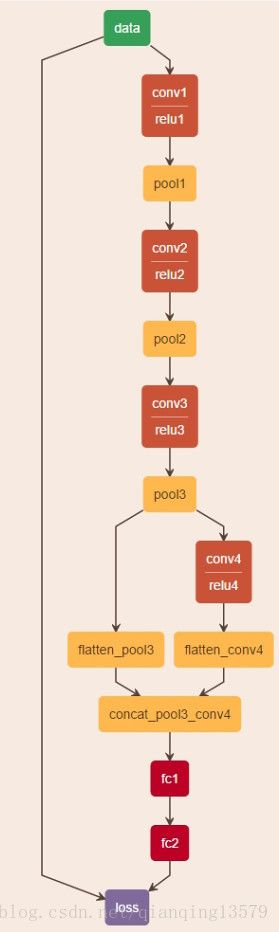
以人脸识别经典的DeepID[1]模型为例,DeepID结构图：

论文见参考文献[1]

我们可以看出，全连接层fc1层就是对应DeepID结构图中的160维的DeepID特征，也就是我们要学习的特征，也就是softmax loss 概率公式中的 x x ,而全连接层fc2层每个节点对应一个wi w i 和 bi b i (可以将每个节点看成一个特征图，只不过特征图大小为1*1),全连接层相当于做内积运算(所以prototxt中全连接层的type名叫InnerProduct)，每个节点的输出就可以写成： wTix+bi w i T x + b i ,由于全连接层fc2层的输出就是softmax loss层的输入，所以 wTix+bi w i T x + b i 就是公式中e的指数。

由softmax loss概率公式我们可以知道，每一类概率对应一个 wTix+bi w i T x + b i ，所以公式中 i i 的个数等于类别数，所以fc2层的输出向量的维度需要与类别数相等，这就是为什么分类问题中softmax loss层前面一层全连接层的节点数为什么总要等于类别数的原因。

论文思想

我们知道人脸识别最理想的特征是最大类内距小于最小类间距。在SphereFace之前的triplet loss,center loss也是为了达到这个目的。论文中的A-softmax loss并不是新的loss,其实还是原始的softmax loss,只是对原始的softmax loss公式做了变换，导致softmax loss层的输入发生了变化，也就是最后一层全连接层fc2的输出发生了变化。
原始softmax loss层中最后一个全连接层的输出是wTx+b w T x + b ,而a-softmax中，最后一个全连接层的输出由 wTx+b w T x + b 转化为 ||w||||x||cos(θ)+b | | w | | | | x | | c o s ( θ ) + b ,如果对w归一化，且b=0,则可以简化为 ||x||cos(θ) | | x | | c o s ( θ ) ，这就导致了学习到的特征 x x 发生了变化 (DeepID模型中x就是倒数第2个全连接层fc1层表示的特征向量)。论文通过该方法将特征x x 转换到了球体空间，使得学习到的人脸特征具有更好的可区分性。

---

实验

训练样本

本文实验中的训练样本采用了CASIA,对人脸进行了对齐(使用参考文献[2]中的算法),并做了crop。crop后的部分训练样本如下：

训练及测试

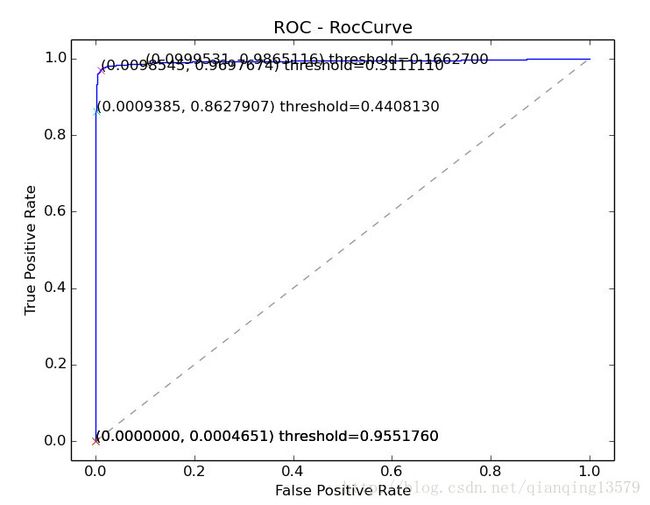
训练用的网络结构和训练参数直接使用了作者提供的，收敛速度较慢，最终softmax_loss降到2.0左右。在LFW上测试，对于每个pair,计算两个人脸提取出来的fc5层特征的cosine距离，并根据距离画ROC曲线

由ROC曲线可以看出，SphereFace的效果还是不错的。

2017-10-19 19:56:59

---

参考文献

[1] [2014 CVPR] Deep Learning Face Representation from Predicting 10,000 Classes
[2] [2014 CVPR] One Millisecond Face Alignment with an Ensemble of Regression Trees

---

非常感谢您的阅读，如果您觉得这篇文章对您有帮助，欢迎扫码进行赞赏。