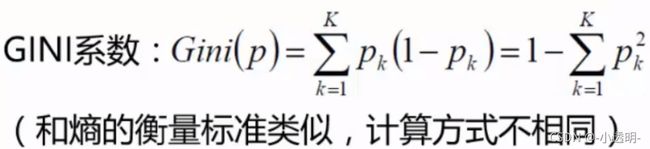Python数据分析与机器学习实战＜八＞决策树、随机森林

目录

决策树原理概述

树模型

决策树

树的组成

决策树的训练和测试

选择节点（即如何进行特征划分？）

衡量标准---熵

公式： Pi为取到某个类别的概率​

熵的图像

如何决策一个节点的选择？

决策树构造实例

信息增益率

ID3（信息增益）缺点

C4.5（信息增益率）<考虑自身熵值>

CART(使用GINI系数来做衡量标准)

 决策树的剪枝策略

对连续值

剪枝策略

为什么剪枝？

策略

决策树涉及的参数

树的可视化与sklearn简介

可视化显示需要的工具

sklearn

sklearn参数选择

GridSearchCV(网络搜索交叉验证)常用属性

集成算法---随机森林

Ensemble learning(集成算法)

Bagging模型

特征重要性衡量

随机森林优势

Boosting(提升模型)

Stacking(堆叠模型)

---

决策树原理概述

树模型

决策树

从根节点开始一步步走到叶子节点（决策）。所有数据最终都会落在叶子节点，既可以做分类又可以做回归。（分类树和回归树）。该算法与其他算法相比 ，便于可视化展示与分析！

树的组成

根节点：第一个选择点

非叶子节点与分枝：中间过程

叶子节点：最终的决策结果

节点：增加节点相当于在数据中切一刀

决策树的训练和测试

训练阶段：从给定的训练集构造出来一棵树（从根节点开始选特征，如何进行特征切分）

测试阶段：根据构造出来的树模型从上到下走一遍就好了

一旦构造好了决策树，n那么分类或者预测任务就很简单了，只需要走一遍就可以了，难点在于 如何构造一棵树。

选择节点（即如何进行特征划分？）

选根节点（最重要的）：目标是根节点能最好的将数据分为两类。可以通过一种衡量方法，计算不同特征进行分支选择后的分类情况，找出最好的当根节点。

选次重要的节点：除去跟节点，比较出剩下的效果最后的做次节点，依次类推。

衡量标准---熵

熵：表示随机变量的不确定性（说白了就是物体内部的混乱程度（就是高中化学里的那个意思））

熵值越高，越混乱，不确定性越强，效率低。就像在杂货店里买东西。

熵越低，就像在专卖店买东西，几乎百分之百能买到。

公式： Pi为取到某个类别的概率

 由于Pi的范围是0~1的，log函数0~1区间的特点：概率越大，即越趋近于1，对应的熵值越小；相反，概率越小，越趋近于0，对应的熵值越大。前面的负号是因为，0~1，log都为负，加上使得结果都变为正的了。

熵的图像

由图可以看出，p=0/1时，熵为0，随机变量此时是确定的；=0.5时不确定性最大。（就像抛硬币的时候）

如何决策一个节点的选择？

信息增益（ID3算法）：表示特征X使得类Y的不确定性的下降程度（分类后，希望结果是同类的在一起）

例如：原本熵值为10，决策后，熵值变成8了，则信息增益为：2

遍历所有特征，看那个的信息增益最大，选它作为根节点。（依次类推）

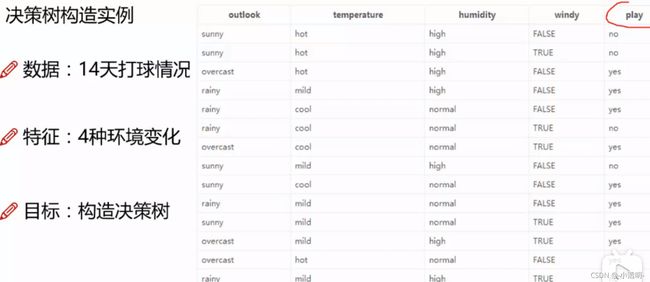
决策树构造实例

决策：最终是否去打球了

不同特征做根节点（需要一个指标进行判断）

log的底数是几是不影响熵值得比较的，sklearn中是2，所以这里以2为例计算 

 overcast中是一个很纯净的数据，都是yes（因此熵为0）

没有决策前的熵为0.940

找出信息增益最大的做根节点 ，剩余三个节点同理

信息增益率

ID3（信息增益）缺点

 当有一个特征：比如编号ID（1，2,3,4,5,6,7,8,9,10,11,12,13,14）算它的熵值时，会出现该类特征下面分了好多类，每一类中的数据都很少，因此会出现最后比较后它的熵最优，而导致误判（此类特征是没有用的）

C4.5（信息增益率）<考虑自身熵值>

即计算ID自身的熵-log（1/14）

CART(使用GINI系数来做衡量标准)

越确定的，GINI系数越小。

 决策树的剪枝策略

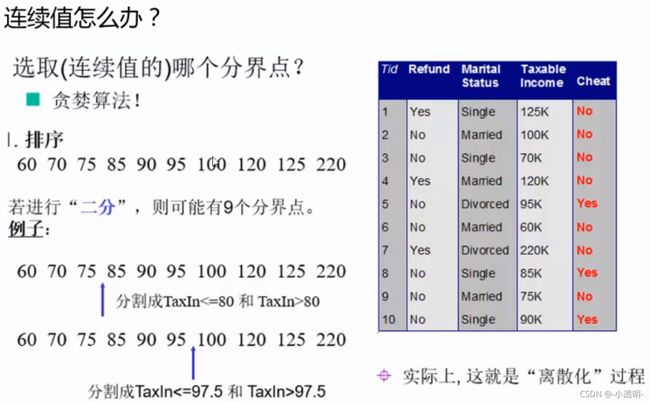
对连续值

 ‘二分’：在某个地方切一刀，将数据分成两类。不一定在最中间切

剪枝策略

为什么剪枝？

决策树的过拟合风险（训练集几乎完全重合，但测试效果很差）太大，理论上可以完全分得开数据

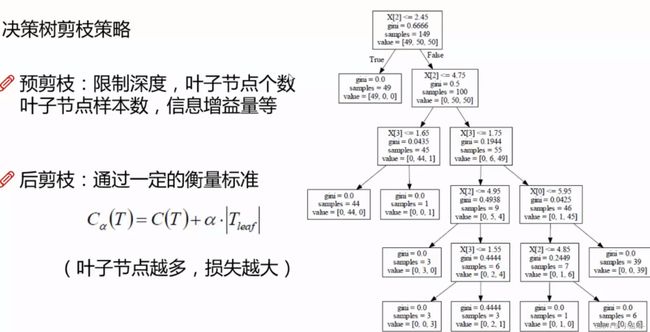
策略

预剪枝：边建立决策树边进行剪枝（更实用，可以控制树的深度）

后剪枝：建立完决策树后再进行剪枝

若指定树的深度为3，则下面的信息都会被剪掉。这也是最常指定的参数。

若指定叶子节点个数为5时，从上到下标号，大于5的叶子会被剪掉

叶子结点样本数:例如每个叶子结点下有8个样本，限制叶子节点样本10，则<10的节点不继续分裂

以上三个是最常用的（限制一个阈值）

阈的意思是界限，故阈值又叫临界值，是指一个效应能够产生的最低值或最高值

后剪枝中：（叶子节点越多，损失越大）

Cα（T）、C(T):当前损失，=样本个数*gini系数（所有叶子结点加在一起）

α*|Tleaf|：|Tleaf|为叶子节点个数，α：系数（越大，叶子数越小）用来限制叶子节点个数

目标：使这个式子整体越小越好

后剪枝策略就是：建立完决策树后，指定一系列衡量标准，对每个节点来说，根据标准决定其是否分裂。预剪枝更易实现，因此用的更多

决策树涉及的参数

  gini系数

其中，4和5 最常用

%matplotlib inline


import matplotlib.pyplot as plt
import pandas as pd
# 导入加州房价数据集
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
print(housing.DESCR)# descr(iption)数据的描述

print(housing.data.shape)# 数据大小（2万多条数据，每个数据8个属性）
print(housing.data[0])

(20640, 8)
[   8.3252       41.            6.98412698    1.02380952  322.
    2.55555556   37.88       -122.23      ]

树的可视化与sklearn简介

from sklearn import tree # 决策树模块
dtr = tree.DecisionTreeRegressor(max_depth=2)# 实例化树模型（指定最大深度=2）
dtr.fit(housing.data[:,[6,7]],housing.target)# 构造一个树（第一个参数，选择第6、7列的所有行数据，第二个参数 结果值）

DecisionTreeRegressor(max_depth=2)

可视化显示需要的工具

下载地址   http://www.graphviz.org/Download..php，首先需要下载 stable_windows_10_cmake_Release_x64_graphviz-install-2.49.3-win64（我的电脑是64位），安装后将bin所在路径配置到path中即可。

另外还需要 pip install pydotplus

#创建dot对象
dot_data = \
    tree.export_graphviz(
        dtr, # 树的名字（需指定）
        out_file = None,
        feature_names = housing.feature_names[6:8], # 特征名字（需指定）
        filled = True,
        impurity = False,
        rounded = True
    )
# 另外还需要 pip install pydotplus
#导入dot绘图包
import pydotplus
 
#创建绘图对象
graph = pydotplus.graph_from_dot_data(dot_data)
graph.get_nodes()[7].set_fillcolor("#FFCCFF")
from  IPython.display import Image
Image(graph.create_png())

# 还可以
#绘制图像保存到本地
graph.write_png("E:/cluster/dtr_white_background.png")# .png的清晰度比.jpg高

# 保存好后会打印 True

sklearn

如果数据在百万级以下都可以用sklearn做，毕竟用的人多，有报错问题容易搜到。

官网： Installing scikit-learn — scikit-learn 1.0.1 documentation

里面有许多画好的图，可以直接拿来改一改使用。（Example里）用API搜算法，有具体参数的介绍等。英文不可避免（慢慢适应）

sklearn参数选择

from sklearn.model_selection import train_test_split
# 数据切分,0.1做测试集，random_state指定随机状态使每次运行代码结果都是一样的
data_train,data_test,target_train,target_test=train_test_split(housing.data,housing.target,test_size=0.1,random_state=42)
dtr=tree.DecisionTreeRegressor(random_state=42)# 构造树模型
dtr.fit(data_train,target_train)

dtr.score(data_test,target_test)

0.6310922690494536

from sklearn.ensemble import RandomForestRegressor
rfr = RandomForestRegressor(random_state=42)
rfr.fit(data_train,target_train)
rfr.score(data_test,target_test)

0.8103647255362918

GridSearchCV(网络搜索交叉验证)常用属性

grid_scores_在sklearn0.20版本中已被删除，取而代之的是cv_results_

best_score_ ：最佳模型下的分数
best_params_ ：最佳模型参数
grid_scores_ ：模型不同参数下交叉验证的平均分
cv_results_ ： 具体用法模型不同参数下交叉验证的结果
best_estimator_ : 最佳分类器之所以出现以上问题

# from sklearn.grid_search import GridSearchCV
# 如果版本高于等于0.20说明是grid_search模块已被弃用改为了.model_selection
from sklearn.model_selection import GridSearchCV
# 循环遍历寻找最好的参数组合
# min_samples_split指定最少叶子节点（才能继续分裂）
# n_estimators 数的个数
tree_param_grid = { 'min_samples_split': list((3,6,9)),'n_estimators':list((10,50,100))}# 共9组
# 以字典的格式传入CV，cv:进行几次交叉验证
# cv=5，即把划分出来的训练集划分为5份
grid = GridSearchCV(RandomForestRegressor(),param_grid=tree_param_grid,cv=5)
grid.fit(data_train,target_train)
grid.cv_results_,grid.best_params_,grid.best_score_

【Output】
({'mean_fit_time': array([ 0.75877185,  4.39268751,  9.34879155,  0.84088254,  4.59808102,
         10.63340549,  0.94916453,  4.57520771,  7.97047873]),
  'std_fit_time': array([0.00448832, 0.23598786, 0.2733354 , 0.06125801, 1.01391708,
         0.62752858, 0.07324958, 0.37666237, 0.29606443]),
  'mean_score_time': array([0.00878448, 0.04867611, 0.09793692, 0.00879049, 0.04268732,
         0.09823651, 0.00918202, 0.04307933, 0.06851883]),
  'std_score_time': array([0.00038347, 0.00477828, 0.01004586, 0.00074195, 0.00737429,
         0.00939864, 0.00117278, 0.00811912, 0.00275596]),
  'param_min_samples_split': masked_array(data=[3, 3, 3, 6, 6, 6, 9, 9, 9],
               mask=[False, False, False, False, False, False, False, False,
                     False],
         fill_value='?',
              dtype=object),
  'param_n_estimators': masked_array(data=[10, 50, 100, 10, 50, 100, 10, 50, 100],
               mask=[False, False, False, False, False, False, False, False,
                     False],
         fill_value='?',
              dtype=object),
  'params': [{'min_samples_split': 3, 'n_estimators': 10},
   {'min_samples_split': 3, 'n_estimators': 50},
   {'min_samples_split': 3, 'n_estimators': 100},
   {'min_samples_split': 6, 'n_estimators': 10},
   {'min_samples_split': 6, 'n_estimators': 50},
   {'min_samples_split': 6, 'n_estimators': 100},
   {'min_samples_split': 9, 'n_estimators': 10},
   {'min_samples_split': 9, 'n_estimators': 50},
   {'min_samples_split': 9, 'n_estimators': 100}],
  'split0_test_score': array([0.78661217, 0.80953583, 0.80998301, 0.78628887, 0.80839827,
         0.80906404, 0.78796628, 0.81186877, 0.8097875 ]),
  'split1_test_score': array([0.78233906, 0.79859971, 0.80176887, 0.78767127, 0.79963782,
         0.80145192, 0.78051626, 0.80013444, 0.79984993]),
  'split2_test_score': array([0.7866243 , 0.80440609, 0.80609848, 0.7875195 , 0.8015914 ,
         0.80087879, 0.78875309, 0.80002153, 0.80166061]),
  'split3_test_score': array([0.79285639, 0.80834936, 0.81117322, 0.79167763, 0.81001392,
         0.81150607, 0.80059767, 0.81010792, 0.81067907]),
  'split4_test_score': array([0.7766219 , 0.80546073, 0.80830034, 0.79187606, 0.8049548 ,
         0.80761553, 0.79202819, 0.80622118, 0.80665746]),
  'mean_test_score': array([0.78501076, 0.80527035, 0.80746478, 0.78900667, 0.80491924,
         0.80610327, 0.7899723 , 0.80567077, 0.80572691]),
  'std_test_score': array([0.0053709 , 0.00381982, 0.00331971, 0.00231296, 0.00392501,
         0.00422312, 0.00651234, 0.00491876, 0.00431166]),
  'rank_test_score': array([9, 5, 1, 8, 6, 2, 7, 4, 3])},
 {'min_samples_split': 3, 'n_estimators': 100},
 0.807464783817624)

rfr = RandomForestRegressor(min_samples_split=3,n_estimators=100,random_state=42)
rfr.fit(data_train,target_train)
rfr.score(data_test,target_test)

0.8096755084021448

pd.Series(rfr.feature_importances_,index=housing.feature_names).sort_values(ascending=False)

MedInc        0.524244
AveOccup      0.137907
Latitude      0.090685
Longitude     0.089255
HouseAge      0.053957
AveRooms      0.044554
Population    0.030329
AveBedrms     0.029069
dtype: float64

集成算法---随机森林

Ensemble learning(集成算法)

目的：使机器学习效果更好，上面的决策树是单个算法，集成并不是一种新的机器学习算法，而是很多中机器学习算法聚集在一起。以下有3种集成算法：

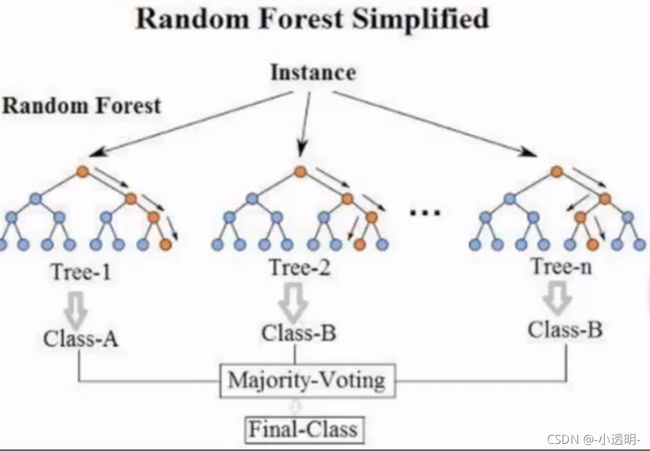
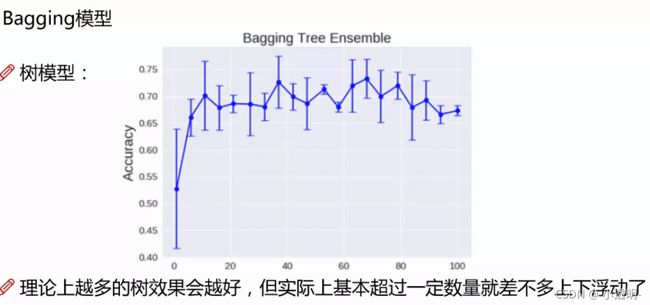
Bagging模型

训练多个分类器取平均 并行

 全称：bootstrap aggregation（即并行训练一堆分类器）

最典型的代表就是随机森林了

    随机：数据采样随机，特征选择随机。

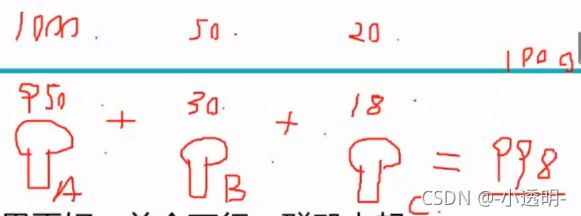
        随机1 每棵树  在原始数据上有放回的随机选取相同百分比的数（一般0.6~0.8）输入不同

        随机2   每棵树  特征的选择也是随机的（保证特征量和数据量相同即可）

有了这两个随机，每棵树基本都不同，最终结果也会不一样

    森林：很多个决策树并行放在一起

 

分类任务：最终取众数 ；回归：最终可以取个平均

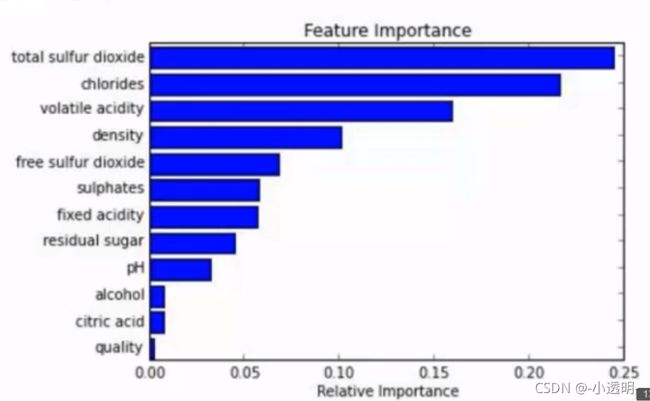
特征重要性衡量

 之所以要随机，是要保证其泛化能力（是指机器学习算法对新鲜样本的适应能力），如果每棵树都一样，是没有意义的。

随机森林优势

1.能够处理很高维（很多特征）的数据，，并且不用做特征选择。

2.在训练完后，能够给出那些特征比较重要。（(有监督问题中)如果一个原始特征破坏掉后建立模型的错误率跟没有破坏之前的差不多则说明，原始这个特征不那么重要，反之，说明很重要。如图,sklearn 通过这种方式判断重要性的，当然还有其他方式）

 

3.容易做成并行化方法，速度比较快。

4.可以进行可视化展示，便于分析。

集成模型--- 树模型（KNN范化能力很差）

一二百个树就可以了

Boosting(提升模型)

串行算法（从弱学习器开始加强，通过加权进行训练）

 分类器的分类效果越好，权值越大

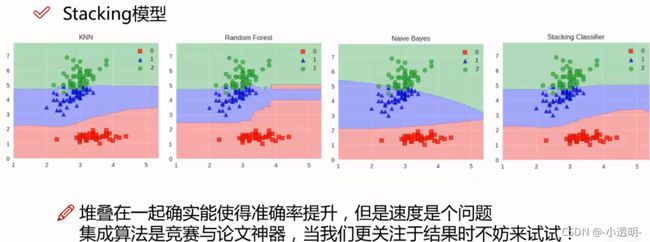
Stacking(堆叠模型)

聚合多个分类或回归模型（可以分阶段做）