传统推荐系统之协同过滤算法（UserCF、ItemCF）

1、概述

\quad \quad 协同过滤(Collaborative Filtering)算法是指基于用户行为数据设计的推荐算法，主要包括：

1、基于邻域的算法：UserCF（基于用户的协同过滤算法）、ItemCF（基于物品的协同过滤算法）

2、隐语义模型(LFM)：基于矩阵分解的推荐算法

3、基于图的随机游走算法：PersonalRank

\quad \quad 在这些方法中，最著名的、在业界中得到最广泛应用的算法是基于邻域的方法，而基于邻域的方法主要包括下面两种算法。

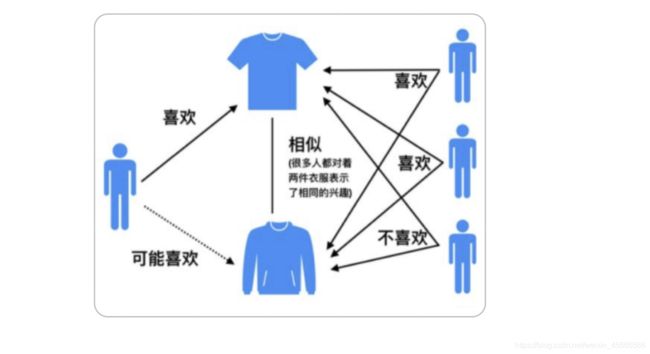
• 基于用户的协同过滤算法(UserCF)：这种算法给用户推荐和他兴趣相似的其他用户喜欢的物品。
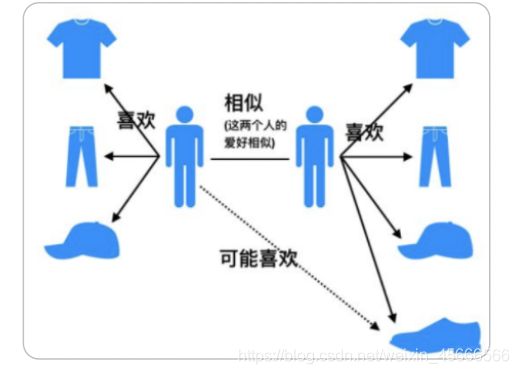
• 基于物品的协同过滤算法(ItemCF)：这种算法给用户推荐和他之前喜欢的物品相似的物品。

2、相似性度量方法

\quad \quad 不管是UserCF还是ItemCF算法，非常重要的一步就是计算用户和用户或者物品和物品之间的相似度，下面综述一下常用的相似性度量方法。
1、杰卡德（Jaccard)相似系数

\quad \quad 此指标是衡量两个集合的相似度的一种指标。两个用户u和v交互商品交集的数量占这两个用户交互商品并集的数量的比例，称为这两个集合的杰卡德相似系数，用符号$si{m}_{uv}$表示，
$$si{m}_{uv}=\frac{|N(u)\cap N(v)|}{|N(u)\cup N(v)|}$$

其中，$N(u)、N(v)$分别表示用户u、v交互商品的集合。

由于杰卡德相似系数一般无法反映具体用户的评分喜好信息， 所以常用来评估用户是否会对某商品进行打分， 而不是预估用户会对某商品打多少分。
2、余弦相似度

\quad \quad 余弦相似度衡量了两个向量的夹角，夹角越小越相似。首先从集合的角度描述余弦相似度，相比于Jaccard公式来说就是分母有差异，不是两个用户交互商品的并集的数量，而是两个用户分别交互的商品数量的乘积，公式如下

$$si{m}_{uv}=\frac{|N(u)\cap N(v)|}{\sqrt{|N(u)|\ast |N(v)|}}$$

\quad \quad 从向量的角度进行描述，令矩阵 A为用户-商品交互矩阵(因为是TopN推荐并不需要用户对物品的评分，只需要知道用户对商品是否有交互就行)，即矩阵的每一行表示一个用户对所有商品的交互情况，有交互的商品值为1没有交互的商品值为0，矩阵的列表示所有商品。若用户和商品数量分别为m,n 的话，交互矩阵A 就是一个 m行 n列的矩阵。此时用户的相似度可以表示为(其中$u.v$ 指的是向量点积)：
$$si{m}_{uv}=cos(u,v)=\frac{u.v}{|u|\ast |v|}$$

上述用户-商品交互矩阵在现实情况下是非常的稀疏了，为了避免存储这么大的稀疏矩阵，在计算用户相似度的时候
一般会采用集合的方式进行计算。理论上向量之间的相似度计算公式都可以用来计算用户之间的相似度，但是会根据
实际的情况选择不同的用户相似度度量方法。
这个在具体实现的时候， 可以使用 cosine_similarity 进行实现：

from sklearn.metrics.pairwise import cosine_similarity

两者区别：

\quad \quad 杰卡德相似度适用于隐式反馈数据（0，1布尔值/是否加入购物车），余弦相似度适合用户评分数据（实数值）。

3、皮尔逊相关系数

所以相比余弦相似度，皮尔逊相关系数通过使用用户的平均分对各独立评分进行修正，减小了用户评分偏置的影响。
具体实现， 我们也是可以调包， 这个计算方式很多， 下面是其中的一种：

from scipy.stats import pearsonr

3 、基于用户的协同过滤算法(UserCF)

3.1 UserCF算法原理

\quad \quad 俗话说“物以类聚、人以群分”，拿看电影这个例子来说，如果你喜欢《蝙蝠侠》、《碟中谍》、《星际穿越》、《源代码》等电影，另外有个人也都喜欢这些电影，而且他还喜欢《钢铁侠》，则很有可能你也喜欢《钢铁侠》这部电影。所以说，当一个用户 A 需要个性化推荐时，可以先找到和他兴趣相似的用户群体 G，然后把 G 喜欢的、并且 A 没有听说过的物品推荐给 A，这就是基于用户的协同过滤算法。

3.2 UserCF算法步骤

\quad \quad 根据上述基本原理，我们可以将基于用户的协同过滤推荐算法拆分为两个步骤：

1、找到与目标用户兴趣相似的用户集合。
2、找到这个集合中用户喜欢的、并且目标用户没有听说过的物品推荐给目标用户。

3.2.1 用户相似度计算

1、发现兴趣相似的用户

\quad \quad 通常用 Jaccard 公式或者余弦相似度计算两个用户之间的相似度（这里我们用余弦相似度）。设 N(u) 为用户 u 喜欢的物品集合，N(v) 为用户 v 喜欢的物品集合，那么 u 和 v 的相似度是多少呢?计算流程如下：

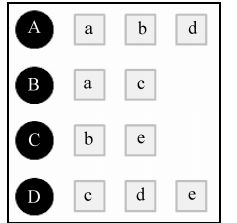
1、假设目前共有4个用户： A、B、C、D；共有5个物品：a、b、c、d、e。用户与物品的关系（用户喜欢物品）如下图所示：

• 余弦相似度公式：$$\frac{|N(u)\cap N(v)|}{\sqrt{|N(u)|\ast |N(v)|}}$$
• 若直接基于用户行为记录计算，则会由于很多用户相互之间并没有对同样的物品产生过行为，即很多时候$|N(u)\cap N(v)|=0$，就会造成时间内上的浪费。
• 因此，可以再建立下面的 “物品—用户” 的倒排表，对于每个物品都保存对该物品产生过行为的用户列表。
  2、建立 “物品—用户” 的倒排表

即下图的右半部分

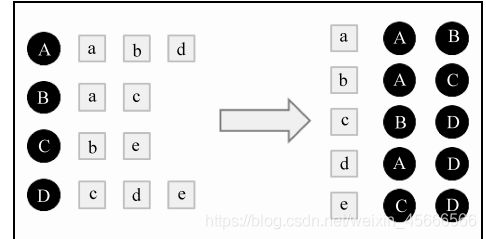
3、然后对于每个物品，喜欢他的用户，两两之间相同物品加1。

\quad \quad 例如喜欢物品 a 的用户有 A 和 B，那么在矩阵中他们两两加1。如下图所示：

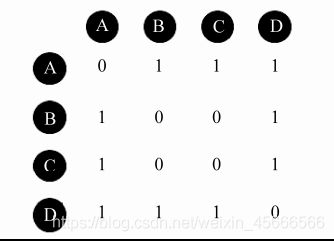
此矩阵乃为相似度公式的分子部分。

4、计算用户两两之间的相似度，得到相似度矩阵

\quad \quad 上面的矩阵仅仅代表的是公式的分子部分。以余弦相似度为例，对上图进行进一步计算：

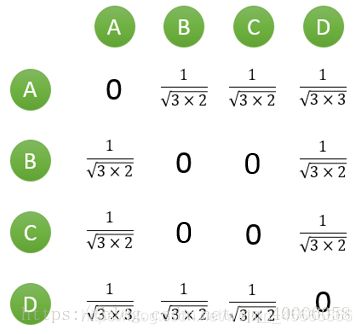
到此，计算用户相似度就大功告成，可以很直观的找到与目标用户兴趣较相似的用户。

3.2.2 生成推荐列表

\quad \quad 首先需要从矩阵中找出与目标用户 u 最相似的 K 个用户，用集合 S(u, K) 表示，将 S 中用户喜欢的物品全部提取出来，并去除 u 已经喜欢的物品。对于每个候选物品 i ，用户 u 对它感兴趣的程度用如下公式计算：

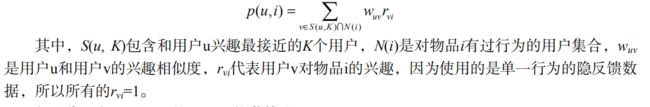
注：在一些需要用户给予评分的推荐系统中，则$r_{vi}$系数表示代入用户评分。

举个例子，假设我们要给 A 推荐物品，选取 K = 3 个相似用户，相似用户则是：B、C、D，那么他们喜欢过并且 A 没有喜欢过的物品有：c、e，因此可以把这两个物品推荐给用户A。根据UserCF算法，用户A对物品c、e的兴趣是

$$p(A,c)=w_{AB}+w_{AD}=\frac{1}{\sqrt{6}}+\frac{1}{\sqrt{9}}=0.7416$$
$$p(A,c)=w_{AC}+w_{AD}=\frac{1}{\sqrt{6}}+\frac{1}{\sqrt{9}}=0.7416$$

看样子用户 A 对 c 和 e 的喜欢程度可能是一样的，在真实的推荐系统中，只要按得分排序，取前几个物品就可以了。

3.3 优化_User-IIF算法

\quad \quad 如果两个用户都购买过热门物品，这丝毫不能说明他们兴趣相似，因为绝大数人都会购买热门物品。换句话说，两个用户对冷门物品采取过同样的行为更能说明他们兴趣的相似度。因此，John S.Breese 在论文中提出了一下公式，根据用户行为计算用户的兴趣形似度：
$$W_{uv}=\frac{{\sum }_{i\in |N(u)\cap N(v)|}\frac{1}{log1+|N(i)|}}{\sqrt{|N(u)||N(v)|}}$$

\quad \quad 可以看出$\frac{1}{log1+|N(i)|}$惩罚了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响。

4、基于物品的协同过滤算法(ItemCF)

4.1 ItemCF算法原理

\quad \quad ItemCF的基本思想是预先根据所有用户的历史偏好数据计算物品之间的相似性，然后把与用户喜欢的物品相类似的物品推荐给用户。比如物品a和物品c非常相似，因为喜欢a的用户同时也喜欢c，而用户A喜欢a，所以把c推荐给用户A。ItemCF算法并不利用物品的内容属性计算物品之间你的相似度，主要通过分析用户的行为记录计算物品之间的相似度，该算法认为，物品a和物品c具有很大的1相似度是因为喜欢物品a的用户大都喜欢物品c。

4.2 ItemCF算法步骤

\quad \quad 根据上述基本原理，我们可以将基于物品的协同过滤推荐算法拆分为两个步骤：

1、计算物品之间的相似度
2、根据物品的相似度和用户的历史行为给用户生成推荐列表。

4.2.1 物品相似度计算

1、建立用户-物品的倒排表
2、对于每个用户，将用户列表中的物品两两组合，并在共现矩阵中加1
3、遍历共现矩阵，计算出物品相似度矩阵W，计算公式如下：
$$W_{i,j}=\frac{|N(i)\cap N(j)|}{\sqrt{|N(i)||N(j)|}}$$

其中，N(i),N(j)分别是喜欢物品i和物品j的用户数。

4.2.2 生成推荐列表

通过以下公式计算用户u对一个物品j的兴趣 ：
$$p_{u,j}=\sum _{i\in N(u)\cap S(j,K)}{W}_{j,i}{r}_{u,i}$$

其中，N(u)是用户喜欢的物品的集合，S(j,K)是和物品j最相似的K个物品的集合，$w_{j,i}$是物品j和i的相似度，$r_{u,i}$是用户u对物品i的兴趣。

4.3 优化_ItemCF-IUF算法

1、相似度矩阵的计算中引入对活跃用户的惩罚（活跃用户对物品相似度的贡献应该小于不活跃的用户 ），增加IUF参数即用户活跃度对数的倒数的参数，来修正物品相似度的计算公式
$$W_{i,j}=\frac{{\sum }_{u\in |N(i)\cap N(j)|}\frac{1}{log1+|N(U)|}}{\sqrt{|N(i)||N(j)|}}$$

2、对于过于活跃的用户，往往忽略他们的兴趣列表。

3、将ItemCF的相似度矩阵按最大值归一化，可以提高推荐的准确率和覆盖率
$$W_{i,j}=\frac{W_{i,j}}{{\max }_j{W}_{i,j}}$$

​

4.4 优缺点

• 推荐结果中长尾物品丰富，适用于用户个性化需求强烈的领域
• 可以利用用户的历史行为给推荐结果做出解释
• 用户有新行为，就会实时导致推荐结果的实时变化

5、 实战

1、数据集
\quad \quad 本次实践使用了电影评分数据集，数据中包含了943个用户对1682个电影的10W条评分数据。

2、处理数据集，将数据转换成字典格式

import pandas as pd
# 常用路径变量config
train_data = './mid_data/train.data'
sim_user_user = './mid_data/sim_user_user.txt'
# 训练数据集处理 -> dict{user_id:{item_id:rating}}
def gene_train_data(nrows):
    # 读取数据
    df=pd.read_csv('D:/BaiduNetdiskDownload/tuijian/day15_CF/ml-100k/u.data'
                   , sep='\t'
                   , nrows=nrows # 指定行数，取多少行，若全取，则不管
                   , names=['user_id', 'item_id',  'rating', 'timestamp'])
    d = dict()
    for _, row in df.iterrows():
        # print(row)
        user_id = str(row['user_id'])
        item_id = str(row['item_id'])
        rating = row['rating']
        if d.get(user_id, -1) == -1:
            d[user_id] = {item_id:rating}
        else:
            d[user_id][item_id] = rating
    return d

5.1 UserCF

from cf.utils import gene_train_data
import math
# 获取用户数据
d=gene_train_data(nrows=None)
# 设置两个参数
train_data = './mid_data/train.data' # 存放训练数据
sim_user_user = './mid_data/sim_user_user.txt' # 存储用户之间的相似度矩阵
# 将训练数据存到磁盘中,需要新建一个mid_data Directory
# with open(train_data,'w') as f:# 写数据，写完以后注释掉
#     f.write(str(d))
# 1、获取用户之间的相似度，返回相似性矩阵
# 1.1 根据用户_物品字典，直接计算用户之间的余弦相似度
# 缺点：有可能会出现相似度为0的数，造成时间上的浪费
def user_normal_similarity(d):
    w = dict()
    for u in d.keys():
        if u not in w:
            w[u] = dict()
        for v in d.keys():
            if u == v: # 过滤掉相同用户
                continue
            # 余弦相似度
            w[u][v] = len((set(d[u])) & set(d[v])) # 分子，交集
            w[u][v] /= math.sqrt(len(set(d[u]))*len(set(d[v]))*1.0)

    # print(w)
    # print(w['196'])
    # # 获取所有的用户的分值
    # print('all user cnt；', len(w.keys()))
    # print('user 196 sim_user_cnt:', len(w['196']))
    return w
# 1.2 优化计算用户与用户之间的相似度：建立物品到用户的倒排表即user->item ->item->user
# 即将相似度为0的用户剔除掉
def user_sim(d):
    # 物品——用户倒排表
    item_user = dict()
    for u,items in d.items():
        for i in items.keys():
            if i not in item_user: #
                item_user[i] = set()
            item_user[i].add(u)
    # print(item_user)
    # 存放统计用户与用户共同的item数量
    C = dict()
    for i,users in item_user.items():
        for u in users:
            if C.get(u, -1) == -1:
                C[u] = dict()
            for v in users:
                if u == v:
                    continue
                if C[u].get(v,-1) == -1:
                    C[u][v]=0
                C[u][v] += 1
    # 倒排使用完之后，将其从内存中删除
    del item_user
    for u,sim_users in C.items():
        for v,cuv in sim_users.items():
            C[u][v] = cuv / math.sqrt(len(set(d[u]))*len(set(d[v]))*1.0)
    # 获取所有的用户的分值
    # print('all user cnt；', len(C.keys()))
    # print('user 196 sim_user_cnt:', len(C['196']))
    return C


# 将相似用户的矩阵存到磁盘中
# with open(sim_user_user,'w') as fw:# 写数据
#     fw.write(str(C))
# 1.3 优化-User-IIF算法:用户相似度
def user_IIF_sim(d):
    # 物品——用户倒排表
    item_user = dict()
    for u,items in d.items():
        for i in items.keys():
            if i not in item_user: #
                item_user[i] = set()
            item_user[i].add(u)
    # print(item_user)
    # 存放统计用户与用户共同的item数量
    E = dict()
    for i,users in item_user.items():
        for u in users:
            if E.get(u, -1) == -1:
                E[u] = dict()
            for v in users:
                if u == v:
                    continue
                if E[u].get(v,-1) == -1:
                    E[u][v]=0
                E[u][v] += 1 / math.log(1+len(users)*1.0)
    # 倒排使用完之后，将其从内存中删除
    del item_user
    for u,sim_users in E.items():
        for v,euv in sim_users.items():
            E[u][v] = euv / math.sqrt(len(set(d[u]))*len(set(d[v]))*1.0)
    # 获取所有的用户的分值
    # print('all user cnt；', len(E.keys()))
    # print('user 196 sim_user_cnt:', len(E['196']))
    return E
# 定义推荐的方法
def recommend(user,d,C,k):
    rank = dict()
    # 获取用户评论过的电影
    iterated_items=d[user].keys()
    for v,cuv in sorted(C[user].items(),key=lambda x:x[1],reverse=True)[0:K]:
        for i,rating in d[v].items():
            if i in iterated_items: #购买过的商品过滤掉
                continue
            elif rank.get(i,-1) == -1:
                rank[i]=0
            # 最终物品的打分
            rank[i]+=cuv*rating
    return rank

# 定义main函数
if __name__=='__main__':
    # read train_data
    d=dict()
    with open(train_data,'r') as ft:
        d=eval(ft.read())
    # read user sim matrix
    C=dict()
    with open(sim_user_user,'r') as fc:
        C=eval(fc.read())
    user = '196'
    K=5
    rank = recommend(user,d,C,K)
    print(sorted(rank.items(),key=lambda x:x[1],reverse=True)[0:10])

结果：

[('100', 5.545984234329238), ('204', 5.0131651029552575), ('210', 4.681208237993316), ('56', 4.468729380017961), ('514', 4.465965676051493), ('211', 4.465965676051493), ('168', 4.450455647285777), ('603', 4.34194476753129), ('50', 4.318231315499943), ('709', 4.284969468004466)]

5.2 ItemCF

import math
# 定义一个item和item的 sim path
train_data = './mid_data/train.data'
sim_item_item = './mid_data/sim_item_item.txt' # 存放物品之间的相似度矩阵
# 1、计算物品与物品之间的相似度矩阵
def item_sim(d):
    # 相似度矩阵,数据结构：{item：{sim_item:sim_score,sim_item2:sim_score2}}
    C = dict()
    # item对应的用户集合
    N = dict()
    # 获取数据d,d.items()数据结构：d:{user_id:{item_id1:rating,item_id2:rating}}
    d=dict()
    with open(train_data, 'r') as ft:
        d = eval(ft.read())
    for u,items in d.items():
        for i in items:
            if N.get(i,-1) == -1:
                N[i] = 0
            N[i] += 1 # 相当于有一个用户，+1
            if C.get(i,-1) == -1:
                C[i] = dict()
            for j in items:
                if i==j : # 如果两个物品相等，过滤掉
                    continue
                elif C[i].get(j,-1) == -1:
                    C[i][j] = 0
                C[i][j] += 1 # 分子部分
    for i,related_items in C.items():
        for j,cij in related_items.items():
            C[i][j] = cij / math.sqrt(N[i]*N[j]) # N[i],N[j]分别表示i，j的用户量
    return C
# 将物品相似度矩阵存到磁盘中，记得存储完注释掉
# with open(sim_item_item,'w') as fw:
#     fw.write(str(C))
# 1.2 优化-ItemCF-IUF算法:物品相似度
def itemCF_IUF_sim(d):
    # 相似度矩阵,数据结构：{item：{sim_item:sim_score,sim_item2:sim_score2}}
    E = dict()
    # item对应的用户集合
    N = dict()
    # 获取数据d,d.items()数据结构：d:{user_id:{item_id1:rating,item_id2:rating}}
    d=dict()
    with open(train_data, 'r') as ft:
        d = eval(ft.read())
    for u,items in d.items():
        for i in items:
            if N.get(i,-1) == -1:
                N[i] = 0
            N[i] += 1 # 相当于有一个用户，+1
            if E.get(i,-1) == -1:
                E[i] = dict()
            for j in items:
                if i==j : # 如果两个物品相等，过滤掉
                    continue
                elif E[i].get(j,-1) == -1:
                    E[i][j] = 0
                E[i][j] += 1 / math.log(1+len(items)*1.0) # 分子部分
    for i,related_items in E.items():
        for j,cij in related_items.items():
            E[i][j] = cij / math.sqrt(N[i]*N[j]) # N[i],N[j]分别表示i，j的用户量
    return E
# 2、生成推荐列表
def recommend_item(d,user_id,C,k):
    rank = dict()
    Ru = d[user_id]
    for i, rating in Ru.items():
        for j,sim_score in sorted(C[i].items(),key=lambda x:x[1],reverse=True)[0:k]:
            if j in Ru:
                # print(j)
                continue
            elif rank.get(j,-1) == -1:
                rank[j] = 0
            rank[j] += sim_score * rating
    return rank


# 主函数
if __name__ == '__main__':
    # read train data
    d = dict()
    with open(train_data, 'r') as ft:
        d = eval(ft.read())
    with open(sim_item_item, 'r') as rf:
        C = eval(rf.read())
    rank=recommend_item(d, user_id='196', C=C, k=5)
    print(sorted(rank.items(), key=lambda x: x[1], reverse=True)[0:10])

结果：

[('204', 22.881496830523623), ('216', 16.61431935263775), ('174', 10.42958180953346), ('121', 10.381711120765363), ('69', 10.155169033376973), ('88', 9.966715500264868), ('210', 8.608562235175), ('237', 8.122115262696923), ('302', 7.540978555119928), ('168', 7.451876357941908)]