迁移学习——Stable Learning via Sample Reweighting

《Stable Learning via Sample Reweighting》学习
arXiv

---

摘要

研究了具有模型错误描述偏差的线性预测模型的学习问题。在这种情况下，输入变量之间的共线性可能会增大参数估计的误差，当训练分布和检验分布不匹配时，会导致预测结果不稳定。
本文从理论上分析了这一基本问题，并提出了一种减少输入变量间共线性的样本加权方法。
我们的方法可以看作是对数据的预处理，以改善设计矩阵的条件，然后它可以结合任何标准的学习方法进行参数估计和变量选择。

一、介绍

当测试数据的分布与训练数据的分布不一致时，大多数机器学习方法的性能就会下降。这是因为传统的学习方法依赖于一个基本的假设，即在训练时提取的数据与测试数据来自相同的底层分布。
然而，在许多实际情况下，这一假设可能会被违背，因为我们对未来将产生的测试数据没有事先的知识。因此，大量假设测试数据分布可用的学习方法(例如迁移学习(Pan, Yang))在这种情况下并不适用。
在本文中，我们考虑了直接解决这个基本问题的稳定学习问题。稳定学习的目标是学习一个在任意数据点$x$上表现一致良好的预测模型。我们实际上需要两个假设:

1. 在目标$y$和预测器$x_p$之间存在一个稳定的结构，该结构在整个分布中保持不变。
2. 外部偏差带来的虚假关联在不同的环境中是不稳定的。

在实践中很常见的是，由于我们收集数据的时间跨度、区域和策略不同，通常会存在这样的虚假关联。
如果只利用稳定结构进行预测，即使未知检验分布与训练分布有显著差异，也能保证良好的预测性能。

稳定学习的主要挑战是在实际应用中，我们不能期望为底层应用问题选择一个完全正确的模型。
我们在本文中表明，如果在训练时使用了不正确的模型(这在实践中是不可避免的)，变量之间的共线性(即两个或多个输入变量之间的线性依赖)的存在会使一个小的错误描述误差膨胀到任意大，从而导致不同分布测试数据的预测性能不稳定。
因此，如何减少共线性在稳定学习问题中是至关重要的
在线性模型中，由于变量的贡献是可互换的，因此评估变量的个体重要性带来了挑战。
处理共线性的主要方法是执行变量选择。基于互信息的方法如(Kononenko 1994;Raileanu和Stoffel, 2004;丁鹏2005;Peng, Long, and Ding 2005)可以看作是数据的预处理。他们基本上是通过最大化所选变量与响应之间的相关性，同时最小化所选变量之间的相关性，来为响应变量选择一个具有代表性和鉴别性的变量子集。
另一种方法是基于正则化技术，由于它们同时在参数估计和变量选择方面取得了良好的性能而受到关注。通过对变量结构的不同假设区分，(Zou and Hastie 2005;Lorbert等人2010;Grave, Obozinski，和Bach 2011)设计惩罚条款，通过约束相关变量要么全部选择，要么根本不选择为“集群”，和方法(Chen et al. 2013;高田，铃木，藤泽2018;Zhou, Jin, and Hoi 2010)只选择单个集群中的一个变量。
这些方法的性能高度依赖于对变量结构的正确假设。
当相关簇中存在非活动变量或多个活动变量时，这些方法要么丢失信息，要么包含非活动变量，导致分布变化导致行为不稳定。
我们首先从理论上分析了错误描述偏差带来的最坏估计误差，并论证了它与共线性的直接联系。
为了缓解变量间的共线性，我们提出了一种新的样本重加权方案。从理论上证明了在理想情况下，存在一组能使设计矩阵接近正交的样本权值。
因此，我们提出了一个样本重加权去相关算子(SRDO)来减少实际中的共线性。具体地说，我们构造一个不相关的设计矩阵$\tilde{\mathbf{X}}$从原始$\mathbf{X}$作为“oracle”，并通过估计底层的不相关分布$\tilde{\mathbf{D}}$和原始分布$\mathbf{D}$的密度比学习样本权重$w(x)$。
该方法可以看作是一种通用的数据预处理方法，改善了底层设计矩阵的条件，以达到预测的目的。学习到的样本权重可以很容易地集成到标准的线性回归方法中，如普通最小二乘回归、Lasso和逻辑回归，以提高它们在不同分布测试数据上的稳定性。
本文的主要贡献如下:

1. 研究了具有模型错误描述的线性模型在测试分布变化情况下的稳定学习问题。这个问题对于需要模型健壮性和稳定性的实际应用是至关重要的。
2. 从理论上证明了预测稳定性与变量间共线性的直接联系，并提出了一种新的样本重加权去相关算子(SRDO)来降低设计矩阵的共线性。
3. SRDO是一种通用的数据预处理方法，可以很容易地集成到各种经典的参数估计、变量选择和预测方法中，在合成数据集和真实数据集上的大量实验表明，它在变化分布下的预测稳定性和精度方面都具有优越的性能。

二、问题和方法

符号: 本文用$n$表示样本容量，$p$表示观测变量的维数。对于任意矩阵$A\in {\mathbb{R}}^{n\times p}$，设${\mathbf{A}}_{i,}$和${\mathbf{A}}_{,j}$分别表示$\mathbf{A}$的第i行和第j列。对于任意向量$\mathbf{v}=(v_1,v_2，\cdot \cdot \cdot ，v_m{)}^{\top }$，设$\Vert \mathbf{v}{\Vert }_1={\sum }_{i=1}^m|v_i|and\Vert \mathbf{v}{\Vert }_2^2={\sum }_{i=1}^m{v}_i^2$。
我们首先定义稳定学习问题如下
问题1。(稳定的学习)
给定目标$y$和$p$输入变量$x=[x_1，\dots ，x_p]\in {\mathbb{R}}^p$，我们的任务是学习一个可以在任意数据点上实现一致小误差的预测模型。
本文在回归和分类线性模型的范围内研究了上述问题。

2.1用于回归的稳定线性模型

我们考虑了具有模型错误描述的线性回归问题。具体来说，我们可以假设目标$y$的生成如下:
$$y=x^{\top }{\bar{\beta }}_{1:p}+{\bar{\beta }}_0+b(x)+ϵ\text{\hspace{1em}(1)}$$
其中$x\in {\mathbb{R}}^p$为输入向量，$b(x)$为依赖于$x$的偏置项，使$|b(x)|\le \delta$，且$ϵ$是方差为${\sigma }^2$的零均值噪声。
在稳定学习中，我们假设生成模型的线性部分是稳定的，对未知的分布漂移不变量，而错误描述偏差$b(x)$可能是不稳定的。在这种意义上，我们希望尽可能准确地估计$\bar{\beta }$。
加上偏置项$b(x)$对于所有$x$都是一致小的性质，我们可以对所有$x$做出可靠的预测。
特别是，分布的变化对于预测目的并不重要。
给定训练数据$\{(x_1,y_1)，\dots ，(x_n,y_n)\}$，其中设计矩阵$\mathbf{X}$来自分布$D$，我们假设$\Vert x_i{\Vert }_2\le 1$。最小二乘回归的标准方法解决了以下问题:
$$\hat{\beta }=\underset{\beta }{\mathrm{argmin}}\sum _{i=1}^n(x_i^{\top }{\beta }_{1:p}+{\beta }_0-y_i{)}^2\text{\hspace{1em}(2)}$$
设${\gamma }^2$为中心协方差矩阵$n^{-1}{\sum }_i(x_i-\bar{x})(x_i-\bar{x}{)}^{\top }$的最小特征值，其中$\bar{x}=n^{-1}{\sum }_i{x}_i$。
本文所考虑的方法是由以下理论结果所驱动的，该结果表明，即使在样本容量无穷大的情况下，模型的错误描述偏差也会产生影响。
命题1。考虑样本容量为无穷大时的最小二乘解:
$$\hat{\beta }=\underset{\beta }{\mathrm{argmin}}{\mathbf{E}}_{(x,y)}(x^{\top }{\beta }_{1:p}+{\beta }_0-y{)}^2\text{\hspace{1em}(3)}$$
由最坏情况扰动误差$|b(x)|\le \delta$引起的估计偏差可以与$\Vert \hat{\beta }-\bar{\beta }{\Vert }_2\le 2(\delta /\gamma )+\delta$一样严重，其中${\gamma }^2$是$\mathbf{E}(x-\mathbf{E}x)(x-\mathbf{E}x{)}^{\top }$的最小特征值。
证明。让$△\beta =\beta -\bar{\beta }，△\hat{\beta }=\hat{\beta }-\bar{\beta }$。我们有
$$△\hat{\beta }=\underset{△\beta }{\mathrm{argmin}}{\mathbf{E}}_x(x^{\top }△{\beta }_{1:p}+△{\beta }_0-b(x){)}^2\text{\hspace{1em}(4)}$$
最优解为:$△{\hat{\beta }}_0={\mathbf{E}}_{x}b(x)-{\mathbf{E}}_x{x}^{\top }△{\hat{\beta }}_{1:p}$。通过消除${\beta }_0$，和让$\tilde{x}=x-\mathbf{E}x$，和$\tilde{b}(x)=b(x)-{\mathbf{E}}_{x}b(x)$，我们有
$$△{\hat{\beta }}_{1:p}=\underset{△{\beta }_{1:p}}{\mathrm{argmin}}({\tilde{x}}^{\top }△{\beta }_{1:p}-\tilde{b}(x){)}^2\text{\hspace{1em}(5)}$$
由此可见,
$$△{\hat{\beta }}_{1:p}=(\mathbf{E}\tilde{x}{\tilde{x}}^{\top }{)}^{-1}\mathbf{E}\tilde{b}(x)\tilde{x}\text{\hspace{1em}(6)}$$
即$\Vert △{\hat{\beta }}_{1:p}{\Vert }_2\le \delta /\gamma$。$|△{\hat{\beta }}_0|\le \delta +\delta /\gamma$。这样我们就得到了期望的界。
由命题1可知，当$\gamma$趋于零时，最坏情况下的估计误差趋于无穷大。这意味着当变量高度共线时，即使训练数据量非常大(或无穷大)，普通的最小二乘法也会产生较差的解。
因此稳定学习的问题是找到稳定的$\hat{\beta }$，以便在无限样本的情况下，对于最坏的$|b(x)|\le \delta$，估计误差是$\Vert \hat{\beta }-\bar{\beta }{\Vert }_2=O(\delta )$和独立于$\gamma$。
这意味着我们容忍由共线性引起的偏差。
为了解决共线性问题，我们提出了一个无限样本情况下的样本权重调整方案如下:
$$\hat{\beta }=\arg \underset{\beta }{\min }{\mathbf{E}}_{(x)\sim D}w(x){\left(x^{\top }{\beta }_{1:p}+{\beta }_0-y\right)}^2,\text{\hspace{1em}(7)}$$
其中$w(x)$为待学习的样本权值。
这就等于
$$\hat{\beta }=\arg \underset{\beta }{\min }{\mathbf{E}}_{(x)\sim \tilde{D}}{\left(x^{\top }{\beta }_{1:p}+{\beta }_0-y\right)}^2,\text{\hspace{1em}(8)}$$
其中
$$\frac{p_{\tilde{D}}(x)}{p_D(x)}=w(x)\text{\hspace{1em}(9)}$$
对于$\tilde{D}$是一个有效的分布，我们有${\mathbf{E}}_{(x)\sim D}[w(x)]=1$。
样品重新加权的目标是改善$\tilde{\gamma }$，其中${\tilde{\gamma }}^2$的最小特征值
$${\mathbf{E}}_{(x)\sim \tilde{D}}(x-{\mathbf{E}}_{x\sim \tilde{D}}x)(x-{\mathbf{E}}_{x\sim \tilde{D}}x{)}^{\top }$$
其中$x$从$\tilde{D}$中提取。
然而，如果${\mathbf{E}}_{(x)\sim D}w(x{)}^2$较大，则随机噪声导致的有限样本误差将受到惩罚$ϵ$。事实上，在加权最小二乘模型中，当$n\to \infty$, 根据Slutsky定理，我们有
$$\sqrt{n}(\hat{\beta }-\bar{\beta })\stackrel{d}{⟶}N(0,\mathbf{Q})\text{\hspace{1em}(10)}$$
其中
$$\mathbf{Q}=E{\left[w\left(x_i\right){\mathbf{x}}_i{\mathbf{x}}_i^{\top }\right]}^{-1}E\left[w{\left(x_i\right)}^2{\mathbf{x}}_i{\mathbf{x}}_i^{\top }{ϵ}_i^2\right]E{\left[w\left(x_i\right){\mathbf{x}}_i{\mathbf{x}}_i^{\top }\right]}^{-1}$$
那么类似于命题1中的分析，随机噪声$ϵ$引起的有限样本估计误差是有界的
$$O\left(n^{-1/2}\sqrt{{\mathbf{E}}_{(x)\sim D}w(x{)}^2}\sigma /\tilde{\gamma }\right)\text{\hspace{1em}(11)}$$
将此结果与命题1结合，有限样本情况下的总估计误差$\Vert \hat{\beta }-\bar{\beta }{\Vert }_2$(由偏置$b(x)$和随机噪声$ϵ$引起)为:
$$O(\delta /\tilde{\gamma })+O\left(n^{-1/2}\sqrt{{\mathbf{E}}_{(x)\sim D}w(x{)}^2}\sigma /\tilde{\gamma }\right)\text{\hspace{1em}(12)}$$
当n很大时。右边第一项是偏差，与训练样本大小n无关，第二项是方差的平方根，方差依赖于n。重加权可以减少偏差项，但总体上增加了方差项。因此，在小样本情况下，当n不太大时，有一个权衡。
如果我们可以使$\tilde{\gamma }$接近1，那么由$b(x)$带来的估计偏差将变成$O(\delta /\tilde{\gamma })=O(1)$，因为我们可以假设错规格误差$\delta$是一个可测量的和有界的“系统”误差，可以被视为一个特定系统的常数值。因此总偏差为
$$\Vert \hat{\beta }-\bar{\beta }{\Vert }_2=O(1)+O\left(n^{-1/2}\sqrt{{\mathbf{E}}_{(x)\sim D}w(x{)}^2}\sigma \right)\text{\hspace{1em}(13)}$$
它与共线性无关，并达到我们讨论过的稳定预测。
以下命题表明，在理想化的情况下，当样本容量为$n\to \infty$时，有可能找到权重$w$，使设计矩阵接近正交(经过定心)。
命题2
设$p_u(x)$是$\mathcal{X}={\mathcal{X}}_1\times \cdot \cdot \cdot \times {\mathcal{X}}_p\subset R^p$上的均匀分布，并假定${\mathbf{E}}_{(x)\sim p_u(x)}\Vert x{\Vert }_2^2<\infty$。
假设每个变量$x_j\in {\mathcal{X}}_j$，向量$x=[x_j]$在$\mathcal{X}$上的密度$p(x)$使$0<2{\gamma }_0\le p_u(x)/p(x)\le {\gamma }_1/2$。对所有$\xi >0$，和$\zeta >0$，存在$N$使所有$n>N$，且概率大于$1-\zeta$，存在$w$使$\Vert w{\Vert }_1=1$， ${\gamma }_0/n\le \Vert w{\Vert }_{\infty }\le {\gamma }_1/n$，和
$$|n^{-1}\sum _i{w}_i(x_{i,j}-c_j)(x_{i,k}-c_k)|\le \xi \text{\hspace{1em}(14)}$$
式中$c_j=n^{-1}{\sum }_i{c}_{i,j}$为各变量$j$的均值，$j\ne k$。
证明。设$w(x)=p_u(x)/p(x)$。对于每一对$1\le j\ne k\le p$，我们知道对于$x=[x^1，\dots ，x^p]\in \mathcal{X}$，
$${\mathbf{E}}_{(x)\sim p(x)}w(x)(x^k-\mathbf{E}{x}^k)(x^{j}k-\mathbf{E}{x}^j)=0\text{\hspace{1em}(15)}$$
我们也知道
$${\mathbf{E}}_{(x)\sim p(x)}w(x)=1$$
因此，根据大数定律，存在概率大于$1-\zeta /p^2$的$N$，当我们绘制$x_i=[x_{i,1}，\dots ，x_{i,p}]$从$p(x)$其中$i=1，\dots n$，我们可以让$w_i=w(x_i)/{\sum }_{j}w(x_j)$然后
$$\left|\frac{1}{n}\sum _{i=1}^n{w}_i(x_{i,j}-c_j)(x_{i,k}-c_k)\right|\le \xi \text{\hspace{1em}(16)}$$
并且
$$\frac{1}{n}\sum _{j}w(x_j)\in [0.5,2]$$
取$(i,j)$对上的联合界，我们得到了想要的结果。
假设我们将所有变量标准化，那么样本协方差矩阵就变成了相关矩阵$R$，命题2表明样本协方差矩阵的非对角元素可以通过$\xi$与样本权$w(x)$使矩阵有任意小的界。
设$M=R-I_p$，通过格什戈林圆定理，可以得到${\gamma }^2\ge 1-\Vert M{\Vert }_{\infty }=1-(p-1)\xi$。因此，通过减少变量之间的两两相关性(也就是，$R$的非对角线元素)，我们可以将最小特征值调整为接近1。
受命题2的启发，我们提出了一个样本重加权去相关算子(SRDO)来降低设计矩阵的共线性。首先，我们使用设计矩阵$\mathbf{X}$来生成一个列- 不相关的一个$\tilde{\mathbf{X}}$，通过执行随机重采样列-明智，这将变量在$\mathbf{X}$中的联合分布分解为$p$个独立的边缘分布在$\tilde{\mathbf{X}}$。
然后，我们可以通过密度比估计(Sugiyama, Suzuki，和Kanamori 2012)来学习样本权重来转移原始的$\mathbf{X}\sim D$到$\tilde{\mathbf{X}}\sim \tilde{D}$。
具体地说，我们设置$\tilde{\mathbf{X}}$为正样本$(Z=1)$，而$\mathbf{X}$为负样本$(Z=0)$，并适合一个概率分类器。
由贝叶斯定理可知，密度比为:
$$w(x)=\frac{p_{\tilde{D}}(\mathbf{x})}{p_D(\mathbf{x})}=\frac{p(\mathbf{x}\mid \tilde{D})}{p(\mathbf{x}\mid D)}=\frac{p(\tilde{D})}{p(D)}\frac{p(Z=1\mid x)}{p(Z=0\mid x)}.\text{\hspace{1em}(17)}$$
注意，前面的$\frac{p(\tilde{D})}{p(D)}$在所有的样本中是常数，所以我们可以忽略它。为了得到$w(x)$的单位均值，我们可以进一步用$w(x)$除以它的均值$\frac{1}{n}{\sum }_{i=1}^{n}w(x_i)$。样本重加权去相关算子(SRDO)的算法可以总结如下:

2.2用于分类的稳定线性模型

除了回归，样本重加权的思想也可以应用于分类问题。为了简单起见，我们使用逻辑回归来考虑二元分类。
在二元分类中，我们有${\beta }^{\top }x\in R,y\in \{\pm 1\}$。
整体损失函数为
$$\sum _{i=1}^n\ln (1+\exp (-{\beta }^{\top }{x}_i{y}_i))\text{\hspace{1em}(18)}$$
给出一个近似的解决方案$\tilde{\beta }$和$\widetilde{p_i}=\tilde{p}(x_i)=1/\left(1+\exp \left(-{\tilde{\beta }}^{\top }{x}_i\right)\right)$，我们可以在该解处使用泰勒展开，将损失函数近似为加权最小二乘如下:
$$\sum _{i=1}^n\widetilde{p_i}(1-\widetilde{p_i})({\beta }^{\top }{x}_i-z_i{)}^2\text{\hspace{1em}(19)}$$
$z_i$是由定义的有效响应
$$z_i\equiv g({\beta }^{\top }{x}_i)+(y-{\beta }^{\top }{x}_i)g^{\prime }({\beta }^{\top }{x}_i)\text{\hspace{1em}(20)}$$
和$g(x)\equiv \log \frac{x}{1-x}$
我们不想让$\mathbf{X}$的协方差矩阵像单位一样接近，而是希望加权协方差矩阵是去相关的。因此，我们仍然可以使用上述方法来估计$w(x)$，只需稍加修改，如下:
$$\tilde{p}(x)(1-\tilde{p}(x))w(x)=\frac{p(Z=1\mid x)}{p(Z=0\mid x)}\text{\hspace{1em}(21)}$$
在实际应用中，我们可以忽略那些可以通过高置信度近似解精确预测的样本，以减小样本权值$w(x)$的方差。然后我们可以解出加权逻辑回归如下:
$$\sum _{i=1}^{n}w(x_i)\ln (1+\exp (-{\beta }^{\top }{x}_i{y}_i))\text{\hspace{1em}(22)}$$

三、实验

在本节中，我们通过模拟研究和两个真实世界的数据集进行回归和分类，来评估我们算法的有效性

3.1基线

对于回归任务，我们将我们的方法与OLS、Lasso (Tibshirani 1996)、Elastic Net (Zou和Hastie 2005)、ULasso (Chen et al. 2013)和IILasso (Takada、Suzuki和Fujisawa 2018)进行比较。前三个基线都是一般意义上的经典方法，而ULasso和IILasso是专门为解决共线性而设计的，可以作为Lasso的延伸:

1. 不相关的套索(ULasso)
   $$\min \Vert Y-\mathbf{X}\beta {\Vert }_2^2+{\lambda }_1\Vert \beta {\Vert }_1+{\lambda }_2{\beta }^T\mathbf{C}\beta$$
   其中$\mathbf{C}\in {\mathbb{R}}^{p\times p}$的每一个元素$C_{jk}=r_{jk}^2$和$r_{jk}=\frac{1}{n}|{\mathbf{X}}_{,j}^T{\mathbf{X}}_{,k}|$
2. 独立解释套索(IILasso)
   $$\min \Vert Y-\mathbf{X}\beta {\Vert }_2^2+{\lambda }_1\Vert \beta {\Vert }_1+{\lambda }_2|\beta {|}^T\mathbf{R}|\beta |$$
   其中$\mathbf{R}\in {\mathbb{R}}^{p\times p}$的每一个元素$R_{jk}=|r_{jk}|/(1-|r_{jk}|)$和$r_{jk}=\frac{1}{n}|{\mathbf{X}}_{,j}^T{\mathbf{X}}_{,k}|$

对于分类任务，我们在基线中用对数似然损失代替平方损失。上述方法具有多个超参数，通过交叉验证对所有参数进行调优。我们将SRDO应用于回归任务中的普通最小二乘，以及分类任务中的逻辑回归，得到我们的结果。
在我们的实验中，我们考虑了$n>p$的情况。而对于相反的情况，人们可能想要使用像Ledoit-Wolf (Ledoit和Wolf 2004)这样的收缩估计器。

3.2模拟研究

3.2.1实验性设置

在模拟研究中，我们通过指定协方差矩阵$\Sigma$的结构，由多元正态分布$X\sim N(0，\Sigma )$生成设计矩阵$\mathbf{X}$。我们可以模拟$\mathbf{X}$的不同关联结构。
具体地说,我们让$\Sigma =\mathrm{Diag}({\Sigma }^{(1)},\cdots ,{\Sigma }^{(q)})$是一个分块对角矩阵，其元素${\Sigma }^{(l)}\in {\mathbb{R}}^{s\times s}$为${\Sigma }_{jk}^{(l)}={\rho }^{(l)}$对于$j\ne k$和${\Sigma }_{jk}^{(l)}=1$对于$j=k$
所以$p$个变量中有$q$组，每组包含$s=\frac{p}{q}$个相关变量。然后我们用$b(\mathbf{X})=\mathbf{X}v$生成偏置项$b(\mathbf{X})$，其中$v$是中心协方差矩阵$n^{-1}{\sum }_i(x_i-\bar{x})(x_i-\bar{x}{)}^{\top }$对应其最小特征值${\gamma }^2$的特征向量。最后，我们生成响应变量$Y$如下:
$$Y=X\bar{\beta }+b(\mathbf{X})+\mathcal{N}(0,1)\text{\hspace{1em}(23)}$$
我们通过定义为$\Vert \bar{\beta }-\hat{\beta }{\Vert }_1$的绝对误差($\beta$误差)来评估估计性能。在训练过程中，我们进行了30次实验，并报告平均$\beta$误差作为估计误差。
对于预测，我们在训练中选择最准确的估计，并计算均方根误差(RMSE)$\frac{1}{n}\sqrt{{\sum }_{i=1}^n(Y_i-{\hat{Y}}_i)}$，我们还进行了30次这个过程，并对结果进行平均。
特别是，在稳定学习中，我们想要评估方法在不同测试环境的变化分布中的性能。为此，我们用固定的${\rho }_{\text{train}}$所有方法，并通过改变测试数据中的$\rho$来产生不同的测试环境。
然后我们报告在各种测试环境下的平均预测误差来表示预测精度，它的标准差来表示预测的稳定性。一个稳定的模型不仅要产生较小的平均预测误差，而且要在不同的测试场景中产生较小的方差。

3.2.2结果

我们对$n,p,s$和${\rho }_{train}$进行了广泛的实验。
从图1和表1中，我们观察和分析如下:

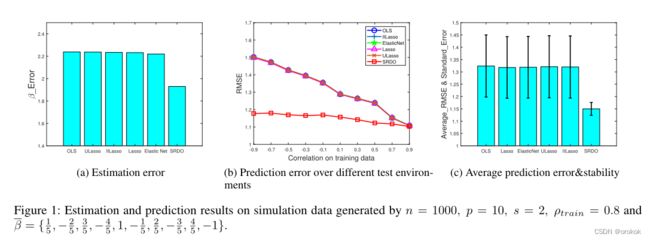
1. 普通最小二乘在误差膨胀方面存在共线性，在大多数情况下性能最差，这与我们的理论分析是一致的。
2. Lasso与OLS没有太大区别，因为我们在模拟中使用了密集的$\bar{\beta }$。最弱的信号的量级为0.2，与最大的信号相当，因此系数收缩机制在这种情况下通常很难工作。
3. Elastic Net的表现略好于其他基线，因为它在共线情况下涉及$l_2$正则化
4. ULasso和IILasso在本实验中并不能很好地解决共线性问题，因为他们假设在相关群中是稀疏的结构(即在多个相关变量中只存在一个活动变量)，这在这里是不满足的。
5. 从图1中我们可以发现，SRDO在变量间相关性强的情况下估计误差最小，在不同的测试设置下预测性能更稳定，达到了稳定学习的目的。注意，在图1 (b)的右端，所有方法都产生了可比较的结果，这与I.I.D.假设相吻合，因为训练数据中的强共线性仍然存在于测试数据中。但是，随着训练分布和测试分布的差异越来越大(从右端到左端)，基线的性能迅速恶化。
6. 从表1可以看出，当训练数据的共线性增强时，我们的方法在估计误差、预测误差和预测稳定性等各方面都比基线得到了更多的改进。

3.3现实回归实验

3.3.1数据集和实验性设置

在这个实验中，我们使用真实世界的房屋销售价格回归数据集(Kaggle)，来自美国King County，其中包括2014年5月至2015年5月之间的房屋销售价格。
为了测试不同算法的稳定性，我们根据房屋建造年份模拟不同的“环境”。
由于架构的流行风格的变化，预测因子的分布以及它们的共线性可能会随着时间的变化而变化，这是相当合理的。

3.3.2结果

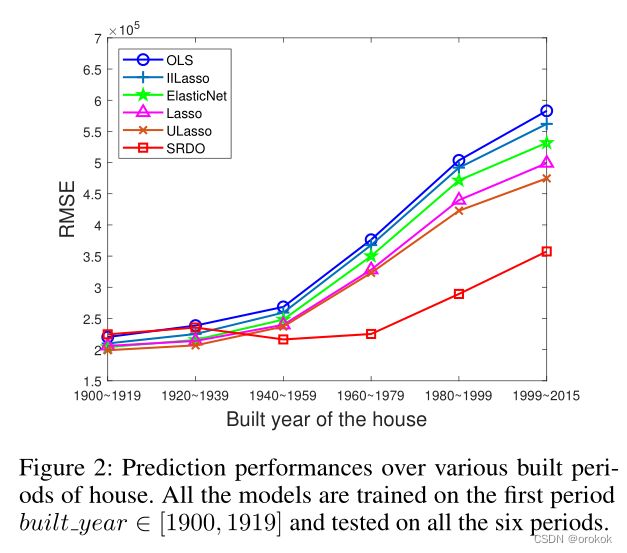
从图2中我们可以发现，与其他基线相比，我们的方法不仅实现了最小的平均误差，而且在不同的测试环境中具有更好的稳定性。结果与我们的假设一致，即通过较长时间跨度收集的数据会发生共线性模式的变化。因此，共线性的去除产生了一个更稳定的分布变化模型。
ElasticNet和Lasso与OLS相比获得了显著的优势，因为它们涉及$l_1$和$l_2$正则化，用于稀疏性和方差减少，这在实际应用中通常是有利的。
一个看似合理的原因是，与ULasso使用$R_{jk}=|r_{jk}|/(1-|r_{jk}|)$，而不是在ULasso中$R_{jk}=r_{jk}^2$，其中$r_{jk}=\frac{1}{n}|X_j^{\top }{X}_k|$是绝对样本相关性。过度惩罚导致所选模型过于稀疏。

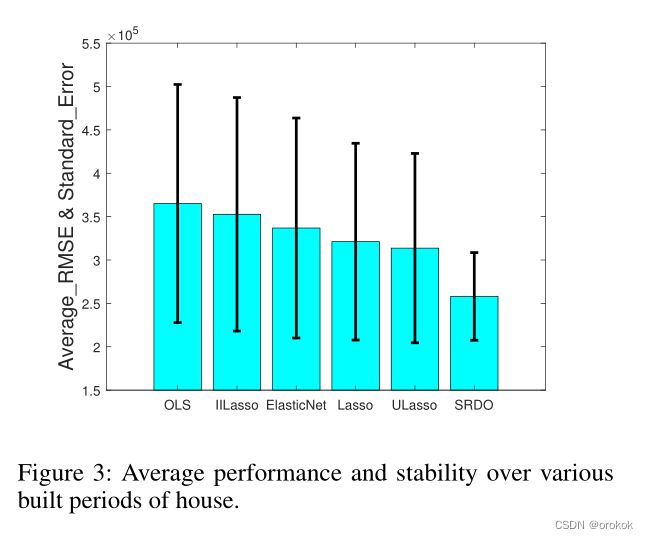
从图3中，我们可以发现所有方法在时间轴上都有明显的误差膨胀。
结果表明，该方法在3-6时间段的性能明显优于基线，且在前两个时间段的性能与基线相当，且分布没有明显变化。因此，在实际使用中，我们的算法更加可靠，尤其是在测试场景中预期会遇到明显的环境变化时。

3.4现实分类实验

3.4.1数据集和实验性设置

微信Ads是2015年9月从腾讯微信App收集的在线广告数据集，包含用户对广告流量的反馈。
为了测试不同算法的稳定性，我们通过用户年龄分层模拟不同的环境，因为我们认为年龄是影响个人兴趣、上网行为等的重要因素。具体来说，我们将数据集按用户年龄分为5个子集。

3.4.2结果

在图4中，我们根据每种方法的AUC绘制了分类性能。
与之前的回归实验类似，我们的方法通常在分布偏移较大且对训练分布和测试分布之间的差异更稳健的情况下有效。
与回归任务相比，AUC的整体改善程度较为温和的一个看似合理的原因是，该数据集的共线性问题不像房屋销售数据那么严重，这对传统方法造成的估计偏差膨胀较小。

总结与讨论

本文研究了具有模型错误描述偏差的线性回归的稳定学习问题。我们提出了一种通过采样重加权来减少共线性对训练数据影响的方法。我们从理论上证明了存在一组最优的样本权值，使设计矩阵在理想情况下接近正交。在更实际的情况下，实证结果表明，当测试数据与训练数据不同时，我们的方法可以提高线性模型的稳定性。我们的方法是一种通用的数据预处理方法，可以无缝集成到经典的线性模型如普通最小二乘和逻辑回归。它为缓解统计估计的共线性问题提供了一种统一的方法。

---

Reference

Stable Learning via Sample Reweighting