【python数据分析】正态分布、正态性检验与相关性分析

手动反爬虫： 原博地址

 知识梳理不易，请尊重劳动成果，文章仅发布在CSDN网站上，在其他网站看到该博文均属于未经作者授权的恶意爬取信息

如若转载，请标明出处，谢谢！

1 正态分布

正态分布概念是由法国数学家和天文学家棣莫弗（Abraham de Moivre）于1733年首次提出的，后由德国数学家Gauss率先将其应用于天文学研究，故正态分布又叫高斯分布

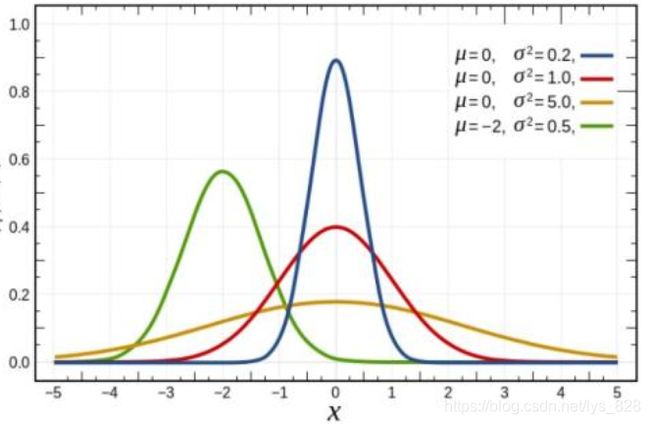
若随机变量$X$服从一个数学期望为$\mu$、方差为${\sigma }^2$的正态分布，记为$N(\mu ，{\sigma }^2)$。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差$\sigma$决定了分布的幅度。当$\mu =0,\sigma =1$时的正态分布是标准正态分布

正态分布对应的概率密度函数：
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(x-\mu {)}^2}{2{\sigma }^2})$$标准正态分布对应的概率密度函数：
$$f(x)=\frac{1}{\sqrt{2\pi }}{e}^{(-\frac{x^2}{2})}$$正态分布曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

• （1）集中性：正态分布曲线的高峰位于正中央，即均数所在的位置
• （2）对称性：正态曲线以均数为中心，左右对称，曲线两端永远不与横轴相交
• （3）均匀变动性：正态曲线有均数所在处开始，分别向左右两侧逐渐均匀下降
• （4）概率为1：曲线与横轴间的面积总等于1，相当于概率密度函数从从负无穷到正无穷的积分值为1，即频率的总和为100%
• （5）$\mu$决定分布的中心位置；$\sigma$越大，曲线越矮胖，总体分布越分散，反之曲线越瘦高，总体分布越集中

对于数据分析过程中的正态分布的理解：

• 并不是所有的数据都是满足正态分布（比如幂律分布）
• 并不是必须满足正态分布才能作分析
• 通过正态分布作为参考去理解事物规律
• 可以通过多种方式进行正态性检验

2 正态性检验

编程环境是在jupyter notebook中

2.1 直方图初判

这里随机生成数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

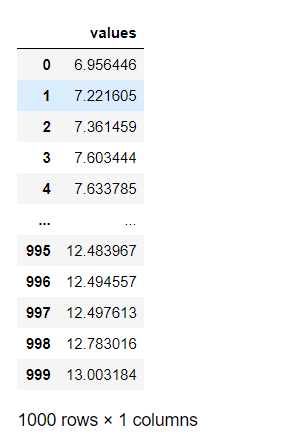
s = pd.DataFrame(np.random.randn(1000)+10,
                columns = ['values'])

fig = plt.figure(figsize=(10,6),dpi = 500)
ax1 = fig.add_subplot(2,1,1)
ax1.scatter(s.index,s.values,edgecolor = 'black')

ax2 = fig.add_subplot(2,1,2)
s.hist(bins = 20,ax = ax2,edgecolor = 'black')
s.plot(kind = 'kde', secondary_y = True, ax = ax2)

输出结果为：（可以发现绘制的密度曲线满足正态分布的曲线样式）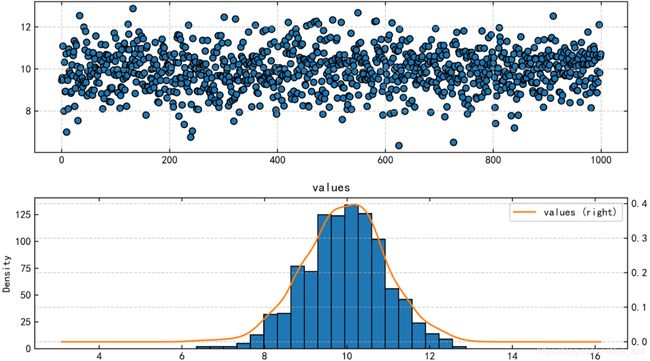

2.2 QQ图

QQ图通过把测试样本数据的分位数与已知分布相比较，从而来检验数据的分布情况

QQ图是一种散点图，对应于正态分布的QQ图，就是由标准正态分布的分位数为横坐标，样本值为纵坐标的散点图

参考直线：四分之一分位点和四分之三分位点这两点确定，看散点是否落在这条线的附近

绘制思路：

• （1） 在做好数据清洗后，对数据进行排序（次序统计量：x(1)
• （2） 排序后，计算出每个数据对应的百分位p(i)，即第i个数据x(i)为p(i)分位数，其中p(i)=(i-0.5)/n （pi有多重算法，这里以最常用方法为主）
• （3）绘制直方图 + QQ图，直方图作为参考

第一步求解样本数据的均值和标准差

s = pd.DataFrame(np.random.randn(1000)+10,
                columns = ['values'])

mean = s['values'].mean()
std = s['values'].std()
print('均值为：{}，标准差为：{}'.format(mean,std))

输出结果为：（由于是随机数，这里的均值和标准差会每次运行都有所不同）

均值为：10.032453869072762，标准差为：1.0290379115139239

第二步，进行数值排序

s_r = s.sort_values(by = 'values').reset_index()
s_r

输出结果为：

第三步，求解p(i)

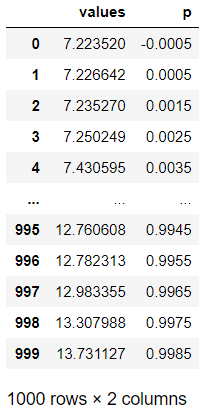
s_r['p'] = (s_r.index - 0.5) / len(s_r)
s_r

输出结果为：

第四步，根据分位数绘制QQ图

st = s['values'].describe()
x1,y1 = 0.25, st['25%']
x2,y2 = 0.75, st['75%']

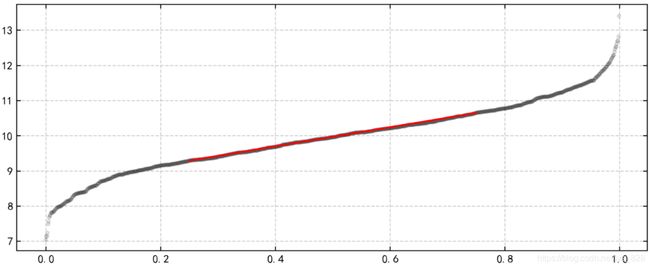
plt.figure(figsize = (10,4),dpi = 200)
plt.plot(s_r['p'],s_r['values'],'k.',alpha = 0.1)
plt.plot([x1,x2],[y1,y2],'-r')

输出结果为：（QQ图绘制完成，数据满足正态分布）

2.3 K-S检验

Kolmogorov–Smirnov test (K-S test) 是比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法

以样本数据的累计频数分布与特定的理论分布比较（比如正态分布），如果两者之间差距小，则推论样本分布取自某特定分布

2.3.1 计算推导

假设检验的问题：
H0:样本的总体分布服从某特定分布
H1:样本的总体分布不服从某特定分布

$F_n(x)\Rightarrow$ 样本的累计分布函数
$F_0(x)\Rightarrow$理论分布的分布函数
$D\Rightarrow F_n(x)与F_0(x)$差值的绝对值最大值，即$D=max(|F_n(x)-F_0(x)|)$

判断依据：$D>D(n,\alpha )$
如果p>0.05则接受H0，p<0.05则拒绝H0，接受H1

第一步，准备样本数据：35位健康男性在未进食之前的血糖浓度，并求解出均值和标准差

data = [87,77,92,68,80,78,84,77,81,80,80,77,92,86,
       76,80,81,75,77,72,81,72,84,86,80,68,77,87,
       76,77,78,92,75,80,78]

df = pd.DataFrame(data, columns = ['value'])
u = df['value'].mean()
std = df['value'].std()
print('均值为：{}，标准差为：{}'.format(u,std))

输出结果为：

均值为：79.74285714285715，标准差为：5.937631024648968

第二步，值计数后按照索引排序，接着求解出累计次数和对应的标准取值

s = df['value'].value_counts().sort_index()
df_s = pd.DataFrame({'血糖浓度':s.index, '次数':s.values})
df_s['累计次数'] = df_s['次数'].cumsum()
df_s['累计频率'] = df_s['累计次数']/len(data)
df_s['标准化取值'] = (df_s['血糖浓度'] - u) / std

df_s

输出结果为：

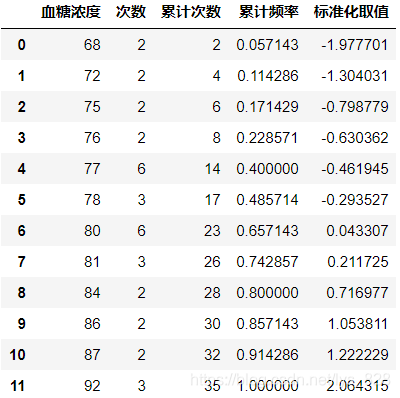
既然求解出标准化的取值，然后对照着下表就可以求解出理论分布对应的值，比如最后一个2.064315，查表后对应的分布值为0.9803，若是负值，比如-1.977701，则先取正值对应的结果后，用1减去就是最终的结果，这里1.977701查表为0.9756，最终的结果就为0.0244。由此可以计算出所有的理论分布

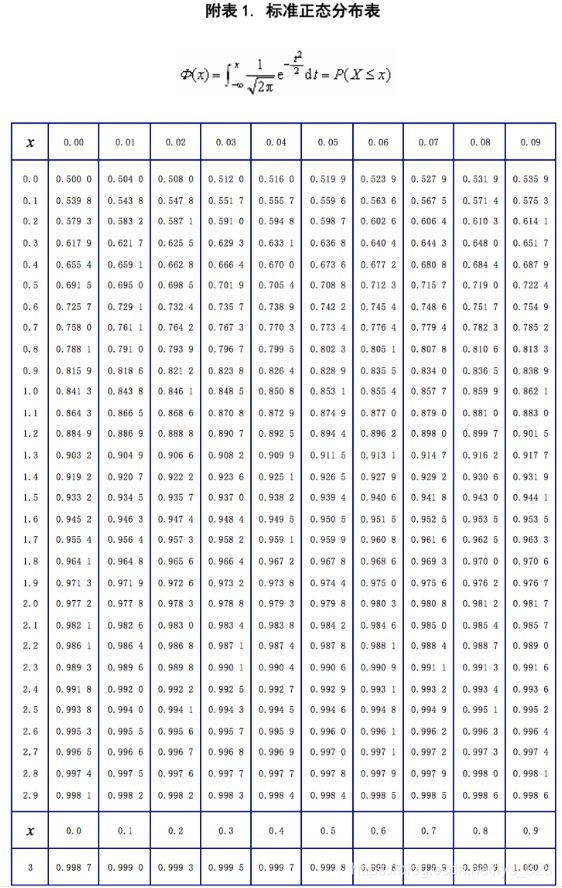
第三步，查表得理论分布后，求解D值

df_s['理论分布'] =[0.0244,0.0968,0.2148,0.2643,0.3228,0.3859,0.5160,0.5832,0.7611,0.8531,0.8888,0.9803]  # 通过查阅正太分布表
df_s['D'] = np.abs(df_s['累计频率'] - df_s['理论分布'])
dmax = df_s['D'].max()
print("实际观测D值为：%.4f" % dmax)
# D值序列计算结果表格

输出结果为：

实际观测D值为：0.1597

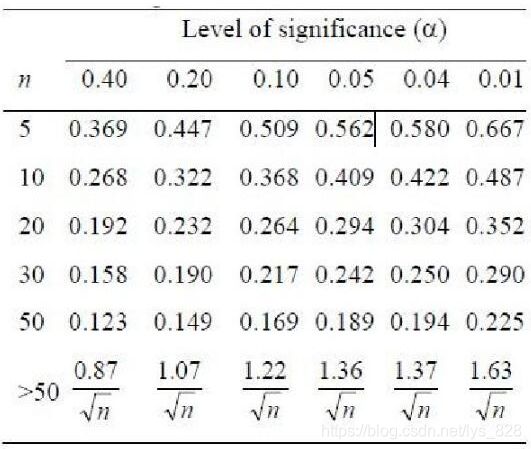
第四步，根据显著性表核实p值大小。参考上表，这里的样本为35，D值为0.1597，那么对应的p值为0.2-0.4之间，要大于0.05，故可以认定样本是服从正态分布的）

2.3.2 代码一步到位

data = [87,77,92,68,80,78,84,77,81,80,80,77,92,86,
       76,80,81,75,77,72,81,72,84,86,80,68,77,87,
       76,77,78,92,75,80,78]

df = pd.DataFrame(data, columns =['value'])
u = df['value'].mean()  
std = df['value'].std()  
stats.kstest(df['value'], 'norm', (u, std))

# .kstest方法：KS检验，参数分别是：待检验的数据，检验方法（这里设置成norm正态分布），均值与标准差
# 结果返回两个值：statistic → D值，pvalue → P值
# p值大于0.05，为正态分布

输出结果为：（pvalue=0.3066，D值也和之前算的值约相等）

KstestResult(statistic=0.1590180704824098, pvalue=0.3066297258358026)

3 相关性分析

相关性分析是指对两个或者多个具备相关性的变量元素进行分析，从而衡量两个因素的相关密切程度

相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析

分析的方式也是有多种：

• （1）图示初判（散点矩阵）
• （2）Pearson相关系数（皮尔逊相关系数）
• （3）Sperman秩相关系数（斯皮尔曼相关系数）

3.1 图示初判

data1 = pd.Series(np.random.rand(50)*100).sort_values()
data2 = pd.Series(np.random.rand(50)*50).sort_values()
data3 = pd.Series(np.random.rand(50)*500).sort_values(ascending = False)
# 创建三个数据：data1为0-100的随机数并从小到大排列，data2为0-50的随机数并从小到大排列，data3为0-500的随机数并从大到小排列，

fig = plt.figure(figsize = (10,4))
ax1 = fig.add_subplot(1,2,1)
ax1.scatter(data1, data2)
plt.grid()
# 正线性相关

ax2 = fig.add_subplot(1,2,2)
ax2.scatter(data1, data3)
plt.grid()
# 负线性相关

输出结果：（这里是两个因素之间的相关性比较）

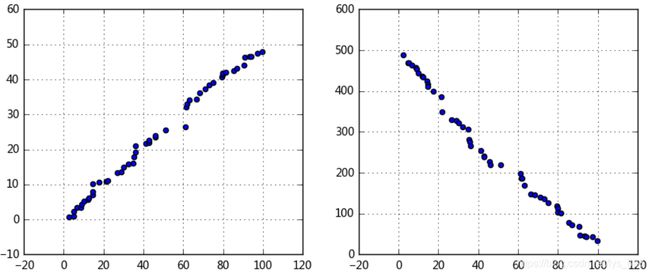
如果是多个因素，那么就可以使用散点矩阵

# （2）散点图矩阵初判多变量间关系

data = pd.DataFrame(np.random.randn(200,4)*100, columns = ['A','B','C','D'])
pd.plotting.scatter_matrix(data,figsize=(8,8),
                  c = 'k',
                 marker = '+',
                 diagonal='hist',
                 alpha = 0.8,
                 range_padding=0.1)

输出结果为：（直接通过分布就可以看出）

3.2 Pearson相关系数

3.2.1 计算推导

最常见的衡量相关性的标准，输出的结果范围为：-1到1之间，0代表着无相关性，负值代表着负相关，正值为正相关。前提：样本必须是正态分布

$0<|r|<1$表示不同程度的线性相关

• $|r|<=0.3\Rightarrow$不存在线性相关
• $0.3<|r|<=0.5\Rightarrow$低度线性相关
• $0.5<|r|<=0.8\Rightarrow$显著线性相关
• $0.8<|r|\Rightarrow$高度线性相关
  
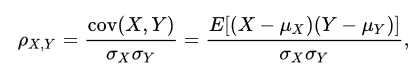
  代码实现：（就是按照上面的公式进行求解）

data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'value1':data1.values,
                     'value2':data2.values})
print(data.head())
print('------')
# 创建样本数据

u1,u2 = data['value1'].mean(),data['value2'].mean()  # 计算均值
std1,std2 = data['value1'].std(),data['value2'].std()  # 计算标准差
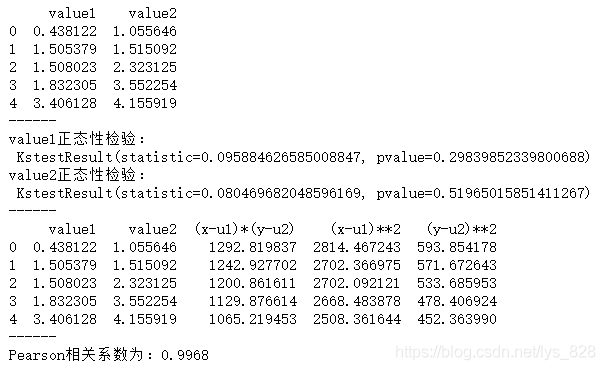
print('value1正态性检验：\n',stats.kstest(data['value1'], 'norm', (u1, std1)))
print('value2正态性检验：\n',stats.kstest(data['value2'], 'norm', (u2, std2)))
print('------')
# 正态性检验 → pvalue >0.05

data['(x-u1)*(y-u2)'] = (data['value1'] - u1) * (data['value2'] - u2)
data['(x-u1)**2'] = (data['value1'] - u1)**2
data['(y-u2)**2'] = (data['value2'] - u2)**2
print(data.head())
print('------')
# 制作Pearson相关系数求值表

r = data['(x-u1)*(y-u2)'].sum() / (np.sqrt(data['(x-u1)**2'].sum() * data['(y-u2)**2'].sum()))
print('Pearson相关系数为：%.4f' % r)
# 求出r
# |r| > 0.8 → 高度线性相关

输出结果为：（先检验正态性，然后按照公式求解即可）

3.2.2 代码一步到位

使用pandas的.corr()方法

data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'value1':data1.values,
                     'value2':data2.values})
print(data.head())
print('------')
# 创建样本数据

data.corr()
# pandas相关性方法：data.corr(method='pearson', min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson

输出结果为：（0.9937，很明显具有相关性）

3.3 Sperman秩相关系数

皮尔逊相关系数主要用于服从正态分布的连续变量，不服从正态分布的变量，分类的关联性可以采用Sperman秩相关系数，也称等级相关系数

计算逻辑：

• 对两个变量成对的取值按照从大到小顺序编秩，Rx代表Xi的秩次，Ry代表Yi的秩次，如果两个值大小相同，则秩次为（index1 + index2）/ 2
• di = Rx - Ry
• Sperman秩相关系数和Pearson相关系数在效率上是等价的

3.3.1 计算推导

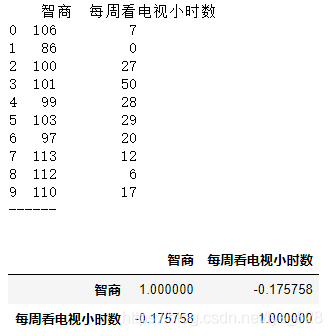
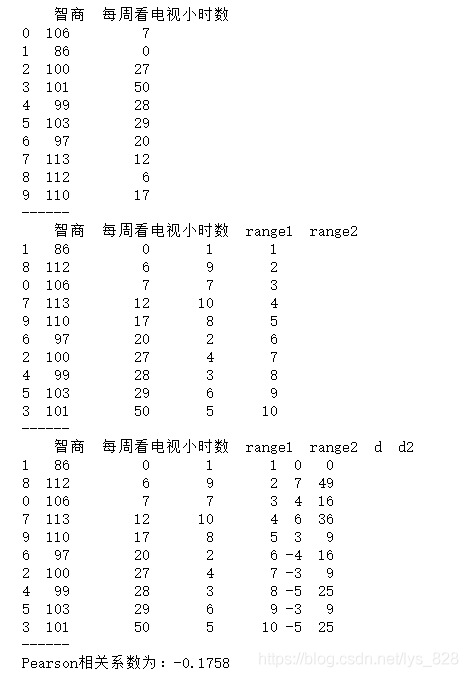
data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,110],
                    '每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})
print(data)
print('------')
# 创建样本数据

data.sort_values('智商', inplace=True)
data['range1'] = np.arange(1,len(data)+1)
data.sort_values('每周看电视小时数', inplace=True)
data['range2'] = np.arange(1,len(data)+1)
print(data)
print('------')
# “智商”、“每周看电视小时数”重新按照从小到大排序，并设定秩次index

data['d'] = data['range1'] - data['range2']
data['d2'] = data['d']**2
print(data)
print('------')
# 求出di，di2

n = len(data)
rs = 1 - 6 * (data['d2'].sum()) / (n * (n**2 - 1))
print('Pearson相关系数为：%.4f' % rs)
# 求出rs

输出结果为：（可以看出每周看电视的小时数和智商没有太大相关性）

3.3.2 代码一步到位

参数中有个method，换一下即可

data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,110],
                    '每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})
print(data)
print('------')
# 创建样本数据

data.corr(method='spearman')
# pandas相关性方法：data.corr(method='pearson', min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson

输出结果为：（可以发现最后的结果和上面的计算推导是一致的）

4 总结

（1）正态分布直接先通过柱状图和密度曲线查看
（2）正态性检验：stats.kstest(df['value'], 'norm', (u, std))
（3）Pearson相关系数：前提是正态分布，data.corr(）
（4）Sperman秩相关系数：不要求是正态分布，data.corr(method='spearman')