C++版NumPy-Eigen库快速入门

零、前言

如果你是一个pythoner，一定知道NumPy操作维度数组和矩阵非常方便，我也在实际开发过程中使用过NumPy来进行过各种算术运算，真是大大地提高了工作效率；曾经一直羡慕pythoner能这么方便的使用NumPy进行各种维度和矩阵运算，直到遇到了Eigen库，它堪称C++版的NumPy，虽然在使用的过程中发现它和NumPy比还有一些不足，但已经很好了，希望它越来越强大。网上虽然已经有了很多有关Eigen的介绍使用，但是自己在使用过程中还是有很多疑惑，于是根据官方提供的文档整理而成这篇文章，希望能够帮助初学者快速入门。

一、Eigen矩阵类

在Eigen中，所有矩阵和向量都是Matrix模板类的对象。向量只是矩阵的一种特殊情况，具有1行或1列。

1、矩阵类模板参数

该矩阵类需要六个模板参数，平时我们主要用到的就前三个参数，剩下的三个参数默认即可。

1>必选模板参数：
Matrix的三个必需模板参数是：
Matrix
Scalar是标量类型，即系数的类型，如果要使用浮点数矩阵，这里就传入float。

RowsAtCompileTime和ColsAtCompileTime是在编译时已知的矩阵的行数和列数。
例如：Matrix4f是一个4x4的浮点矩阵，Eigen定义的方式：
typedef Matrix Matrix4f;

2>可选模板参数
Matrix类其余三个参数是可选的,模板参数的完整列表：
Matrix int RowsAtCompileTime,
int ColsAtCompileTime,
int Options = 0,
int MaxRowsAtCompileTime = RowsAtCompileTime,
int MaxColsAtCompileTime = ColsAtCompileTime>

Options是位字段,用来指定是行优先存储还是列优先存储，默认情况下，矩阵和向量的存储方式是“列优先存储”，可以传值RowMajor和ColMajor。

例如，行优先的3x3矩阵：

MaxRowsAtCompileTime和MaxColsAtCompileTime用来指定矩阵大小的上限，即使在编译时不知道矩阵的确切大小，在编译时也知道固定的上限，这样做的最大原因是避免动态内存分配。

例如，下面矩阵类型使用12个浮点数的普通数组，而没有动态内存分配：
Matrix

2、向量

在Eigen中，向量只是具有1行或1列的矩阵的一种特殊情况，只有1列的向量称为列向量，只有1行的称为行向量。

例如，typedef Vector3f是3个浮点数的(列)向量。Eigen定义如下：
typedef Matrix Vector3f;
行向量的定义：
typedef Matrix RowVector2i;

3、特值动态

Eigen不仅限于其尺寸在编译时已知的矩阵，在RowsAtCompileTime和ColsAtCompileTime模板参数可以采取特殊值Dynamic这表明大小在编译时是未知的，所以必须作为运行时变量来处理。这种大小称为动态 大小；而在编译时已知的大小称为固定 大小。

例如typedef MatrixXd定义为具有动态大小的双精度矩阵，其定义如下：
typedef Matrix MatrixXd;

定义固定数量的行和动态的列数，例如：
矩阵

4、矩阵和向量的初始化

默认构造函数始终可用，从不执行任何动态内存分配，并且从不初始化矩阵系数。可以这样定义：

Matrix3f a;
MatrixXf b;

这里：
a 是一个3×3矩阵，具有未初始化系数的普通float [9]数组，
b 是一个动态大小的矩阵，其大小当前为0 x 0，并且其系数数组尚未分配。
也可以提供采用大小的构造函数。对于矩阵，总是先传递行数。对于矢量，只需传递矢量大小即可。他们分配给定大小的系数数组，但不自行初始化系数：

MatrixXf a(10,15);
VectorXf b(30);

这里：
a 是10x15动态尺寸矩阵，具有已分配但当前尚未初始化的系数。
b 是大小为30的动态大小向量，具有已分配但当前尚未初始化的系数。
为了在固定大小和动态大小的矩阵之间提供统一的API，合法的是在固定大小的矩阵上使用这些构造函数，即使在这种情况下传递大小都没有用。所以这是合法的：

Matrix3f a(3,3);

构造函数来初始化矢量的系数：

Vector2d a(5.0，6.0);
Vector3d b(5.0，6.0，7.0);
Vector4d c(5.0，6.0，7.0，8.0);

5、矩阵和向量的存取

Eigen中的主要系数访问器和变异器是重载的括号运算符。对于矩阵，总是先传递行索引。对于向量，只需传递一个索引。编号从0开始。
示例：

#include 
#include  
using namespace Eigen; 
int main()
{ 
 MatrixXd m(2,2);  
 m(0,0) = 3;  
 m(1,0) = 2.5;  
 m(0,1) = -1;  
 m(1,1) = m(1,0) + m(0,1);  
 std::cout << "Here is the matrix m:\n" << m << std::endl;  
 VectorXd v(2);  
 v(0) = 4;  
 v(1) = v(0) - 1;  
 std::cout << "Here is the vector v:\n" << v << std::endl;
 } 
 程序输出：
 Here is the matrix m:  3  -12.5 1.5 
 Here is the vector v:43

语法m(index)不限于矢量，它也可用于一般矩阵，这意味着在系数数组中基于索引的访问。但是，这取决于矩阵的存储顺序。所有Eigen矩阵默认为列优先存储顺序，但是可以将其更改为行优先。

6、逗号初始化

Eigen矩阵和矢量支持逗号初始化的语法：
例：

Matrix3f m;
m << 1, 2, 3,    
 4, 5, 6,    
 7, 8, 9;
std::cout << m; 
输出结果：
1 2 34 5 67 8 9

7、调整大小

矩阵的当前大小可以通过rows()，cols()和size()检索。这些方法分别返回行数，列数和系数数。调整动态大小矩阵的大小是通过resize()方法完成的。
例：

#include 
#include  
using namespace Eigen; 
int main()
{  
MatrixXd m(2,5);  
m.resize(4,3);  
std::cout << "The matrix m is of size "            << m.rows() << "x" << m.cols() << std::endl;  
std::cout << "It has " << m.size() << " coefficients" << std::endl;  
VectorXd v(2);  v.resize(5);  
std::cout << "The vector v is of size " << v.size() << std::endl;  
std::cout << "As a matrix, v is of size "            << v.rows() << "x" << v.cols() << std::endl;
} 
输出结果：
The matrix m is of size 4x3
It has 12 coefficients
The vector v is of size 5
As a matrix, v is of size 5x1

如果实际矩阵大小不变，则resize()方法为空操作。否则具有破坏性：系数的值可能会更改。

为了API的统一性，所有这些方法仍然可以在固定大小的矩阵上使用。实际上不能调整固定大小的矩阵的大小。尝试将固定大小更改为实际不同的值将触发断言失败。但是以下代码是合法的：
例：

#include 
#include  
using namespace Eigen; 
int main()
{  
Matrix4d m;  
m.resize(4,4); // no operation  
std::cout << "The matrix m is of size "<< m.rows() << "x" << m.cols() << std::endl;
} 
输出结果：
The matrix m is of size 4x4

分配和调整大小
赋值是使用将矩阵复制到另一个矩阵中的操作operator=。Eigen自动调整左侧矩阵的大小，使其与右侧大小的矩阵大小匹配；当然，如果左侧尺寸固定，则不允许调整尺寸。
例：

MatrixXf a(2,2);
std::cout << "a is of size " << a.rows() << "x" << a.cols() << std::endl;
MatrixXf b(3,3);
a = b;
std::cout << "a is now of size " << a.rows() << "x" << a.cols() << std::endl; 
输出结果：
a is of size 2x2a is now of size 3x3

固定尺寸与动态尺寸
什么时候应该使用固定尺寸(例如Matrix4f)，什么时候应该使用动态尺寸(例如MatrixXf)？
简单的答案是：将固定尺寸用于可以使用的非常小的尺寸，将动态尺寸用于较大的尺寸或必须使用的尺寸。对于小尺寸，特别是对于小于(大约)16的尺寸，使用固定尺寸对性能有极大的好处，因为它使Eigen避免动态内存分配。

在内部，固定大小的Eigen矩阵只是一个简单的数组，即
Matrix4f mymatrix;
等于float mymatrix[16];
MatrixXf对象还将其行数和列数存储为成员变量。

当然，使用固定大小的限制是，只有当您在编译时知道大小时，才有可能这样做。对于足够大的尺寸，例如，对于大于(大约)32的尺寸，使用固定尺寸的性能优势变得可以忽略不计。糟糕的是，尝试使用函数内部的固定大小创建非常大的矩阵可能会导致堆栈溢出，因为Eigen会尝试将数组自动分配为局部变量，而这通常是在堆栈上完成的。

二、矩阵和向量算法

Eigen通过常见的C ++算术运算符(例如+，-，*)的重载，或通过诸如dot()，cross()等特殊方法的方式提供矩阵/向量算术运算。对于Matrix类(矩阵和向量)，运算符仅重载以支持线性代数运算。

1、加减

左侧和右侧必须具有相同数量的行和列，还必须具有相同的标量类型，因为Eigen不会自动进行类型升级。操作如下：
二进制运算符+如 a+b
二进制运算符-如 a-b
一元运算符-如 -a
复合运算符+ =如 a+=b
复合运算符-=如 a-=b
例：

#include 
#include  
using namespace Eigen;
 int main()
{  
Matrix2d a; 
 a << 1, 2,       
 3, 4;  
MatrixXd b(2,2); 
 b << 2, 3,       
1, 4;  
std::cout << "a + b =\n" << a + b << std::endl;  
std::cout << "a - b =\n" << a - b << std::endl;  
std::cout << "Doing a += b;" << std::endl;  
a += b;  
std::cout << "Now a =\n" << a << std::endl;  
Vector3d v(1,2,3);  
Vector3d w(1,0,0);  
std::cout << "-v + w - v =\n" << -v + w - v << std::endl;
} 
输出结果：
a + b =
3 5
4 8
a - b =
-1 -1 
2  0
Doing a += b;
Now a =
3 5
4 8
-v + w - v =
-1
-4
-6

2、标量乘法和除法

标量的乘法和除法也非常简单，操作如下：
二进制运算符如 matrixscalar
二进制运算符如 scalarmatrix
二元运算符/如 matrix/scalar
复合运算符* =如 matrix*=scalar
复合运算符/ =如 matrix/=scalar
例：

#include 
#include  
using namespace Eigen; 
int main()
{  
Matrix2d a;  
a << 1, 2,       
3, 4;  
Vector3d v(1,2,3); 
 std::cout << "a * 2.5 =\n" << a * 2.5 << std::endl;  
std::cout << "0.1 * v =\n" << 0.1 * v << std::endl;  
std::cout << "Doing v *= 2;" << std::endl;  
v *= 2;  std::cout << "Now v =\n" << v << std::endl;
} 
输出结果如下：
a * 2.5 =
2.5   5
7.5  10
0.1 * v =
0.1
0.2
0.3
Doing v *= 2;
Now v =
2
4
6

3、转置、共轭和伴随

转置 、共轭 和伴随，矩阵或向量分别通过成员函数transpose()，conjugate()和adjoint()获得。例：

MatrixXcf a = MatrixXcf::Random(2,2);
cout << "Here is the matrix a\n" << a << endl; 
cout << "Here is the matrix a^T\n" << a.transpose() << endl;  
cout << "Here is the conjugate of a\n" << a.conjugate() << endl;  
cout << "Here is the matrix a^*\n" << a.adjoint() << endl;  
输出结果：
Here is the matrix a    
(-1,-0.737) (0.0655,-0.562)
(0.511,-0.0827)  (-0.906,0.358)
Here is the matrix a^T    
(-1,-0.737) (0.511,-0.0827)
(0.0655,-0.562)  (-0.906,0.358)
Here is the conjugate of a    
 (-1,0.737)  (0.0655,0.562) 
(0.511,0.0827) (-0.906,-0.358)
Here is the matrix a^*    
 (-1,0.737)  (0.511,0.0827) 
(0.0655,0.562) (-0.906,-0.358)

对于实矩阵，conjugate()是空运算，所以adjoint()等价于transpose()。

至于基本的算术运算符，transpose()并adjoint()简单地返回一个代理对象没有做实际的换位。如果这样做b = a.transpose()，则会在将结果写入的同时转置b。但是，这样做a = a.transpose()，那么Eigen将在转置完成之前开始将结果写入其中将会出现混叠问题：例：

Matrix2i a; 
a << 1, 2, 3, 4;
cout << "Here is the matrix a:\n" << a << endl;
 
a = a.transpose(); // !!! do NOT do this !!!
cout << "and the result of the aliasing effect:\n" << a << endl;
输出结果：
Here is the matrix a:
1 2
3 4
and the result of the aliasing effect:
1 2
2 4

解决上述问题，可以采用就地转置transposeInPlace()函数，上述中的a = a.transpose()，只需替换为a.transposeInPlace();即可输出正确结果。

MatrixXf a(2,3); 
a << 1, 2, 3, 4, 5, 6;
cout << "Here is the initial matrix a:\n" << a << endl;
a.transposeInPlace();
cout << "and after being transposed:\n" << a << endl;
输出结果：

Here is the initial matrix a:
1 2 3
4 5 6
and after being transposed:
1 4
2 5
3 6

4、矩阵矩阵和矩阵向量乘法

矩阵矩阵乘法operator*，由于向量是矩阵的特例，因此矩阵向量乘积实际上只是矩阵-矩阵乘积的一种特殊情况，向量-向量外积也是如此。所有这些情况仅由两个运算符处理：
二进制运算符如 ab
复合运算符* =的形式a*=b(在右边乘以：a*=b等于a = a*b)
例：

#include 
#include  
using namespace Eigen;
int main()
{  
Matrix2d mat;  
mat << 1, 2,         
3, 4;  
Vector2d u(-1,1), v(2,0);  
std::cout << "Here is mat*mat:\n" << mat*mat << std::endl;  
std::cout << "Here is mat*u:\n" << mat*u << std::endl;  
std::cout << "Here is u^T*mat:\n" << u.transpose()*mat << std::endl;  
std::cout << "Here is u^T*v:\n" << u.transpose()*v << std::endl;  
std::cout << "Here is u*v^T:\n" << u*v.transpose() << std::endl;  
std::cout << "Let's multiply mat by itself" << std::endl;  
mat = mat*mat;  
std::cout << "Now mat is mat:\n" << mat << std::endl;
} 
输出结果：
Here is mat*mat: 
7 10
15 22
Here is mat*u:
11
Here is u^T*mat:
2 2Here is u^T*v:
-2
Here is u*v^T:-
2 -0 2  0
Let's multiply mat by itself
Now mat is mat: 
7 10
15 22

5、点积和叉积

对于点积和叉积，使用dot()和cross()方法。当然，点积也可以作为u.adjoint()* v的1x1矩阵获得。例：

#include 
#include  
using namespace Eigen;
using namespace std;
int main()
{  
Vector3d v(1,2,3);  
Vector3d w(0,1,2);  
 cout << "Dot product: " << v.dot(w) << endl;  
double dp = v.adjoint()*w; // automatic conversion of the inner product to a scalar  
cout << "Dot product via a matrix product: " << dp << endl;  
cout << "Cross product:\n" << v.cross(w) << endl;
} 
输出结果：
Dot product: 8
Dot product via a matrix product: 8
Cross product: 
1
-2 
1

叉积仅适用于大小为3的向量。点积适用于任何大小的向量。当使用复数时，Eigen的点积在第一个变量中是共轭线性的，而在第二个变量中是线性的。

6、基本算术归约运算

Eigen还提供了一些归约运算以将给定的矩阵或向量归约为单个值，例如总和(由sum()计算)，乘积(prod())或最大值(maxCoeff())和最小值(minCoeff())的所有系数。例：

#include 
#include  
using namespace std;
int main()
{  
Eigen::Matrix2d mat;  
mat << 1, 2,         
3, 4;  
cout << "Here is mat.sum():       " << mat.sum()       << endl;  
cout << "Here is mat.prod():      " << mat.prod()      << endl;  
cout << "Here is mat.mean():      " << mat.mean()      << endl; 
cout << "Here is mat.minCoeff():  " << mat.minCoeff()  << endl; 
cout << "Here is mat.maxCoeff():  " << mat.maxCoeff()  << endl;  
cout << "Here is mat.trace():     " << mat.trace()     << endl;
} 
运行结果：
Here is mat.sum():       10
Here is mat.prod():      24
Here is mat.mean():      2.5
Here is mat.minCoeff():  1
Here is mat.maxCoeff():  4
Here is mat.trace():     5

minCoeff和maxCoeff函数的变体，它们通过参数返回相应系数的坐标：
例：

 Matrix3f m = Matrix3f::Random();  
std::ptrdiff_t i, j;  
float minOfM = m.minCoeff(&i,&j);  
cout << "Here is the matrix m:\n" << m << endl;  
cout << "Its minimum coefficient (" << minOfM << ") is at position (" << i << "," << j << ")\n\n";   
RowVector4i v = RowVector4i::Random();  
int maxOfV = v.maxCoeff(&i);  
cout << "Here is the vector v: " << v << endl;  
cout << "Its maximum coefficient (" << maxOfV        << ") is at position " << i << endl; 
输出结果：
Here is the matrix m:     
-1 -0.0827  -0.906 
-0.737  0.0655   0.358  
0.511  -0.562   0.359
Its minimum coefficient (-1) is at position (0,0)
Here is the vector v:  9 -2  0  7
Its maximum coefficient (9) is at position 0

7、操作的有效性

Eigen会检查执行操作的有效性。在编译时检查它们，从而产生编译错误。Eigen将重要消息写在UPPERCASE_LETTERS_SO_IT_STANDS_OUT中。例如：

Matrix3f m;
Vector4f v;
v = m * v;      //编译时错误：YOU_MIXED_MATRICES_OF_DIFFERENT_SIZES

当然，在许多情况下，例如在检查动态大小时，无法在编译时执行检查。然后，Eigen使用运行时断言。如果程序在“调试模式”下运行，则在执行非法操作时该程序将中止并显示一条错误消息，并且如果断言被关闭，它可能会崩溃。例如：

MatrixXf m(3,3);
VectorXf v(4);
v = m * v; //此处的运行时断言失败：“无效的矩阵乘积”

三、数组类和按系数运算

1、数组类

与用于线性代数的Matrix类相反，Array类提供了通用数组。此外，Array类提供了一种执行逐系数运算的简便方法，该运算可能没有线性代数含义，例如向数组中的每个系数添加一个常数或逐个系数地乘以两个数组。

Array是具有与Matrix相同的模板参数的类模板。与Matrix一样，前三个模板参数是必需的：
Array
最后三个模板参数是可选的，与Matrix完全相同。

Eigen还为某些常见情况提供了typedef，其方式类似于Matrix typedef，但有一些细微的差异，因为单词“ array”用于一维和二维数组。Eigen采用以下约定：ArrayNt形式的typedef代表一维数组，其中N和t是大小和标量类型，对于二维数组，使用ArrayNNt形式的typedef，示例：
Array ArrayXf
Array Array3f
Array ArrayXXd
Array Array33d

2、访问数组内的值

括号运算符被重载以提供对数组系数的写和读访问，就像矩阵一样。此外，<<可以使用运算符来初始化数组(通过逗号初始化程序)或打印它们。例：

#include 
#include  
using namespace Eigen;
using namespace std; 
int main()
{  
ArrayXXf  m(2,2);    // assign some values coefficient by coefficient  
m(0,0) = 1.0; 
m(0,1) = 2.0;  
m(1,0) = 3.0; 
m(1,1) = m(0,1) + m(1,0);    // print values to standard output  
cout << m << endl << endl;   // using the comma-initializer is also allowed  
m << 1.0,2.0,       3.0,4.0;       // print values to standard output  
cout << m << endl;
} 
运行结果：
1 2
3 5


1 2
3 4

3、加减

两个数组的加减法与矩阵相同。如果两个数组的大小相同，并且该加法或减法是按系数进行的，则此操作有效。

数组还支持以下形式的表达式：array + scalar将标量添加到数组中的每个系数。这提供了不能直接用于Matrix对象的功能。例：

#include 
#include  
using namespace Eigen;
using namespace std; 
int main()
{  
ArrayXXf a(3,3);  
ArrayXXf b(3,3);  
a << 1,2,3,       
4,5,6,       
7,8,9;  
b << 1,2,3,       
1,2,3,       
1,2,3;         // Adding two arrays  
cout << "a + b = " << endl << a + b << endl << endl;   // Subtracting a scalar from an array  
cout << "a - 2 = " << endl << a - 2 << endl;
} 
运行结果：
a + b =  
2 4 6 
5 7 9 
8 10 12


a-2 = 
-1 0 1 
2 3 4 
5 6 7

4、数组乘法

可以将一个数组乘以标量，这与矩阵的工作方式相同。数组与矩阵根本不同的地方是将两个矩阵相乘。矩阵将乘法解释为矩阵乘积，而数组将乘法解释为系数乘积。因此，当且仅当两个数组具有相同的维数时，它们才能相乘。例：

#include 
#include  
using namespace Eigen;
using namespace std; 
int main()
{  
ArrayXXf a(2,2);  
ArrayXXf b(2,2);  
a << 1,2,       
3,4;  
b << 5,6,       
7,8;  cout << "a * b = " << endl << a * b << endl;
} 
运行结果：
a * b =  
5 12
21 32

5、其他系数运算

所述阵列类定义其他系数为单位的运算除了加法，减法和上述乘法运算符。例如，.abs()方法获取每个系数的绝对值，而.sqrt()计算系数的平方根。两个大小相同的数组，则可以调用.min()来构造其系数为两个给定数组中对应系数的最小值的数组。例：

#include 
#include  
using namespace Eigen;
using namespace std;
 int main()
{ 
ArrayXf a = ArrayXf::Random(5);  
a *= 2;  
cout << "a =" << endl  << a << endl;  
cout << "a.abs() =" << endl  << a.abs() << endl;  
cout << "a.abs().sqrt() =" << endl << a.abs().sqrt() << endl;  
cout << "a.min(a.abs().sqrt()) =" << endl << a.min(a.abs().sqrt()) << endl;
} 
运行结果：
a =    
-2 
-1.47  
1.02
-0.165 
0.131
a.abs()=    
2 
1.47 
1.02
0.165
0.131
a.abs().sqrt()= 
1.41 
1.21 
1.01
0.407
0.362
a.min(a.abs().sqrt())=    
-2 
-1.47  
1.01
-0.165 
0.131

6、在数组和矩阵表达式之间转换

什么时候应该使用Matrix类的对象，什么时候应该使用Array类的对象？

不能对数组应用矩阵运算，也不能对矩阵应用数组运算。因此，如果需要进行线性代数运算(例如矩阵乘法)，则应使用矩阵。

如果需要进行系数运算，则应使用数组。但是，有时却需要同时使用Matrix和Array操作。在这种情况下，需要将矩阵转换为数组或反向转换。无论选择将对象声明为数组还是矩阵，都可以访问所有操作。

矩阵表达式具有.array()方法，可将它们“转换”为数组表达式，因此可以方便地应用按系数进行运算。相反，数组表达式具有.matrix()方法。与所有Eigen表达式抽象一样，这没有任何运行时开销。既.array()和.matrix()可被用作右值和作为左值。

Eigen禁止在表达式中混合矩阵和数组,运算+符的操作数应均为矩阵或均为数组,使用.array()和.matrix()可以轻松地将其转换为另一种。该规则的例外是赋值运算符：允许将矩阵表达式分配给数组变量，或将数组表达式分配给矩阵变量。

下面的示例演示如何通过使用.array()方法对矩阵对象使用数组操作。例如，语句result=m.array()*n.array()取两个矩阵m和n，将它们都转换成一个数组，用系数乘以它们，并将结果赋给矩阵变量result,这是合法的，因为Eigen允许将数组表达式赋给矩阵变量。这种使用情况非常普遍，以至于Eigen为矩阵提供了const.cwiseProduct()方法来计算系数乘积。
例：

#include 
#include  
using namespace Eigen;
using namespace std; 
int main()
{  
MatrixXf m(2,2);  
MatrixXf n(2,2);  
MatrixXf result(2,2);   
m << 1,2,       
3,4;  
n << 5,6,       
7,8;   
result = m * n;  
cout << "-- Matrix m*n: --" << endl << result << endl << endl;  
result = m.array() * n.array();  
cout << "-- Array m*n: --" << endl << result << endl << endl;  
result = m.cwiseProduct(n);  
cout << "-- With cwiseProduct: --" << endl << result << endl << endl;  
result = m.array() + 4;  
cout << "-- Array m + 4: --" << endl << result << endl << endl;
}
 -- Matrix m*n: --
19 22
43 50
-- Array m*n: -- 
5 12
21 32
-- With cwiseProduct: -- 
5 12
21 32
-- Array m + 4: 
--5 6
7 8

同样，如果array1和array2是数组，则表达式array1.matrix() * array2.matrix()将计算其矩阵乘积。
这是一个更高级的示例。该表达式(m.array() + 4).matrix() * m将4加到矩阵中的每个系数m，然后使用来计算结果的矩阵乘积m。类似地，表达式(m.array() * n.array()).matrix() * m计算矩阵的系数之积m和n，然后用结果的矩阵积m。
例：

#include 
#include  
using namespace Eigen;
using namespace std; 
int main()
{  
MatrixXf m(2,2);  
MatrixXf n(2,2);  
MatrixXf result(2,2);   
m << 1,2,       
3,4;  
n << 5,6,       
7,8;    
result = (m.array() + 4).matrix() * m;  
cout << "-- Combination 1: --" << endl << result << endl << endl;  
result = (m.array() * n.array()).matrix() * m;  
cout << "-- Combination 2: --" << endl << result << endl << endl;
} 
运行结果：
-- Combination 1: --
23 34
31 46
-- Combination 2: -- 
41  58
117 170

四、块操作

块是矩阵或阵列的矩形部分，块表达式既可以用作右值，也可以用作左值；与Eigen表达式一样，只要让编译器进行优化，此抽象的运行时成本为零。

1、使用块操作

Eigen中最通用的块操作称为.block()。有两个版本，其语法如下：
块操作:块大小(p,q)，从开始(i,j)
版本构造一个动态大小的块表达式:matrix.block(i，j，p，q) ;
版本构造一个固定大小的块表达式:matrix.block(i，j);

与Eigen一样，索引从0开始。

两种版本均可用于固定大小和动态大小的矩阵和数组。这两个表达式在语义上是等效的。唯一的区别是，如果块大小较小，则固定大小版本通常会为您提供更快的代码，但需要在编译时知道此大小。

以下程序使用动态尺寸和固定尺寸的版本来打印矩阵内几个块的值。例：

#include 
#include  
using namespace std; 
int main()
{  
Eigen::MatrixXf m(4,4);  
m <<  1, 2, 3, 4,        
5, 6, 7, 8,        
9,10,11,12,       
13,14,15,16;  
cout << "Block in the middle" << endl;  
cout << m.block<2,2>(1,1) << endl << endl;  
for (int i = 1; i <= 3; ++i)  
{    
cout << "Block of size " << i << "x" << i << endl;    
cout << m.block(0,0,i,i) << endl << endl; 
 }
} 
运行结果：
Block in the middle 
6  7
10 11
Block of size 1x1
1
Block of size 2x2
1 2
5 6
Block of size 3x3 
1  2  3 
5  6  7 
9 10 11

在上面的示例中，.block()函数用作右值，即仅从中读取。但是，块也可以用作左值，这意味着您可以分配给块。在下面的示例中对此进行了说明。例：

#include 
#include  
using namespace std;
using namespace Eigen; 
int main()
{  
Array22f m;  
m << 1,2,       
3,4;  
Array44f a = Array44f::Constant(0.6);  
cout << "Here is the array a:" << endl << a << endl << endl;  
a.block<2,2>(1,1) = m;  
cout << "Here is now a with m copied into its central 2x2 block:" << endl << a << endl << endl;  
a.block(0,0,2,3) = a.block(2,1,2,3);  
cout << "Here is now a with bottom-right 2x3 block copied into top-left 2x3 block:" << endl << a << endl << endl;
} 

Here is the array a:
0.6 0.6 0.6 0.6
0.6 0.6 0.6 0.6
0.6 0.6 0.6 0.6
0.6 0.6 0.6 0.6
Here is now a with m copied into its central 2x2 block:
0.6 0.6 0.6 0.6
0.6   1   2 0.6
0.6   3   4 0.6
0.6 0.6 0.6 0.6
Here is now a with bottom-right 2x3 block copied into top-left 2x3 block:  
3   4 0.6 0.6
0.6 0.6 0.6 0.6
0.6   3   4 0.6
0.6 0.6 0.6 0.6

尽管.block()方法可用于任何块操作，但对于特殊情况，还有其他方法可提供更专业的API和/或更好的性能。例如，如果您的块是矩阵中的单个整列，则使用下面描述的专用.col()函数让Eigen知道这一点，这可以为其提供优化机会。

2、列和行

单独的列和行是块的特殊情况。Eigen提供了可以轻松解决它们的方法：.col()和.row()。
块操作 方法
第i行matrix.row(i);
第j列: matrix.col(j);

对自变量col()和row()将被访问的列或行的索引。与Eigen一样，索引从0开始。
例：

#include 
#include  
using namespace std; 
int main()
{  
Eigen::MatrixXf m(3,3);  
m << 1,2,3,       
4,5,6,       
7,8,9;  
cout << "Here is the matrix m:" << endl << m << endl;  
cout << "2nd Row: " << m.row(1) << endl;  
m.col(2) += 3 * m.col(0);  
cout << "After adding 3 times the first column into the third column, the matrix m is:\n";  
cout << m << endl;
} 
运行结果：
Here is the matrix m:
1 2 3
4 5 6
7 8 9
2nd Row: 
4 5 6
After adding 3 times the first column into the third column, the matrix m is: 
1  2  6 
4  5 18 
7  8 30

该示例还演示了可以像其他表达式一样将块表达式(此处为列)用于算术运算。

3、与角相关的操作

Eigen还为针对矩阵或数组的角或侧面之一齐平的块提供了特殊的方法。例如，.topLeftCorner()可用于引用矩阵左上角的块。
下表总结了各种可能性：

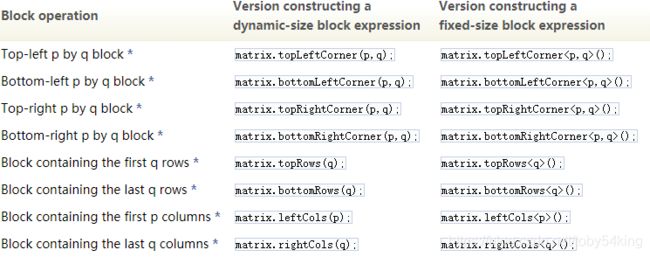
例：

#include 
#include  
using namespace std; 
int main()
{  
Eigen::Matrix4f m;  
m << 1, 2, 3, 4,       
5, 6, 7, 8,       
9, 10,11,12,       
13,14,15,16;  
cout << "m.leftCols(2) =" << endl << m.leftCols(2) << endl << endl;  
cout << "m.bottomRows<2>() =" << endl << m.bottomRows<2>() << endl << endl;  
m.topLeftCorner(1,3) = m.bottomRightCorner(3,1).transpose();  
cout << "After assignment, m = " << endl << m << endl;
} 
运行结果：
m.leftCols(2) = 
1  2 
5  6 
9 10
13 14
m.bottomRows<2>() = 
9 10 11 12
13 14 15 16
After assignment, m =  
8 12 16  4 
5  6  7  8 
9 10 11 12
13 14 15 16

4、向量的块运算

Eigen还提供了一组专门针对矢量和一维数组的特殊情况设计的块操作：

例：

#include 
#include  
using namespace std; 
int main()
{  
Eigen::ArrayXf v(6);  
v << 1, 2, 3, 4, 5, 6;  
cout << "v.head(3) =" << endl << v.head(3) << endl << endl;  
cout << "v.tail<3>() = " << endl << v.tail<3>() << endl << endl;  
v.segment(1,4) *= 2;  
cout << "after 'v.segment(1,4) *= 2', v =" << endl << v << endl;
} 
运行结果：
v.head(3) =
1
2
3
v.tail<3>() = 
4
5
6
after 'v.segment(1,4) *= 2', v = 
1 
4 
6 
8
10 
6

五、Eigen高级初始化

1、逗号初始值设定项

Eigen提供了一种逗号初始化器语法，该语法使用户可以轻松设置矩阵，向量或数组的所有系数。只需列出系数，从左上角开始，从左到右，从上到下移动。需要预先指定对象的大小。例：

Matrix3f m;
m << 1, 2, 3,     4, 5, 6,     7, 8, 9;
std::cout << m;  
输出：1 2 34 5 67 8 9

初始化列表的元素本身可以是向量或矩阵。通常的用途是将向量或矩阵连接在一起。例如，这是将两个行向量连接在一起的方法。请记住，必须先设置大小，然后才能使用逗号初始化程序。例：

RowVectorXd vec1(3);
vec1 << 1, 2, 3;
std::cout << "vec1 = " << vec1 << std::endl;
RowVectorXd vec2(4);
vec2 << 1, 4, 9, 16;
std::cout << "vec2 = " << vec2 << std::endl; 
RowVectorXd joined(7);
joined << vec1, vec2;
std::cout << "joined = " << joined << std::endl; 
运行结果：
vec1 = 1 2 3
vec2 =  1  4  9 16
joined =  1  2  3  1  4  9 16

可以使用相同的技术来初始化具有块结构的矩阵,例：

MatrixXf matA(2,2);
matA << 1,2,3,4;
MatrixXf matB(4,4);
matB << matA，matA / 10，matA / 10，matA;
std :: cout << matB << std :: endl;   
运行结果：
1 2 0.1 0.2  
3 4 0.3 0.4
0.1 0.2 1 2
0.3 0.4 3 4

逗号初始值设定项还可用于填充块表达式，例如m.row(i)。与上面的第一个示例相比，这是一种更复杂的方法来获得相同的结果,例：

Matrix3f m;
m.row(0)<< 1，2，3;
m.block(1,0,2,2)<< 4，5，7，8;
m.col(2).tail(2)<< 6，9;                   
std::cout << m; 
运行结果：
1 2 3
4 5 6
7 8 9

2、特殊矩阵和数组

Matrix和Array类具有像Zero()这样的静态方法，可用于将所有系数初始化为零。有三种变体。第一个变量没有参数，只能用于固定大小的对象。如果要将动态大小对象初始化为零，则需要指定大小。因此，第二个变量需要一个参数，可以用于一维动态大小对象，而第三个变量需要两个参数，可以用于二维对象。以下是三种变体的示例：
例：

std::cout << "A fixed-size array:\n";
Array33f a1 = Array33f::Zero();
std::cout << a1 << "\n\n";  
std::cout << "A one-dimensional dynamic-size array:\n";
ArrayXf a2 = ArrayXf::Zero(3);
std::cout << a2 << "\n\n";  
std::cout << "A two-dimensional dynamic-size array:\n";
ArrayXXf a3 = ArrayXXf::Zero(3, 4);
std::cout << a3 << "\n"; 
运行结果：
A fixed-size array:
0 0 0
0 0 0
0 0 0
A one-dimensional dynamic-size array:
0
0
0
A two-dimensional dynamic-size array:
0 0 0 0
0 0 0 0
0 0 0 0

同样，静态方法Constant(value)会将所有系数设置为value。如果需要指定对象的大小，则附加参数放在value参数之前，如中所示MatrixXd::Constant(rows, cols, value)。方法Random()用随机系数填充矩阵或数组。可以通过调用Identity()获得身份矩阵；此方法仅适用于Matrix，不适用于Array，因为“恒等矩阵”是线性代数概念。该方法LinSpaced(size, low, high)是仅可用于载体和一维数组; 它产生一个指定大小的向量，其系数在low和high之间平均间隔。下面是方法LinSpaced()的示例，该示例打印一张表格，其中包含以度为单位的角度，以弧度为单位的相应角度以及它们的正弦和余弦值。
例：

ArrayXXf table(10, 4);
table.col(0) = ArrayXf::LinSpaced(10, 0, 90);
table.col(1) = M_PI / 180 * table.col(0);
table.col(2) = table.col(1).sin();
table.col(3) = table.col(1).cos();
std::cout << "  Degrees   Radians      Sine    Cosine\n";
std::cout << table << std::endl; 
输出结果：
Degrees   Radians      Sine    Cosine        
0         0         0         1 
10     0.175     0.174     0.985
20     0.349     0.342      0.94
30     0.524       0.5     0.866
40     0.698     0.643     0.766 
50     0.873     0.766     0.643
60      1.05     0.866       0.5   
70      1.22      0.94     0.342      
80       1.4     0.985     0.174
90      1.57         1 -4.37e-08

此示例说明可以将诸如LinSpaced()返回的对象等对象分配给变量(和表达式)。Eigen定义了诸如setZero()，MatrixBase :: setIdentity()和DenseBase :: setLinSpaced()之类的实用程序函数来方便地执行此操作。下面的示例对比了三种构造矩阵的方法。使用静态方法和分配，使用静态方法和逗号初始化程序，或使用setXxx()方法。
例：

const int size = 6;
MatrixXd mat1(size, size);
mat1.topLeftCorner(size/2, size/2)= MatrixXd::Zero(size/2, size/2);
mat1.topRightCorner(size/2, size/2)= MatrixXd::Identity(size/2, size/2);
mat1.bottomLeftCorner(size/2, size/2)  = MatrixXd::Identity(size/2, size/2);
mat1.bottomRightCorner(size/2, size/2) = MatrixXd::Zero(size/2, size/2);
std::cout << mat1 << std::endl << std::endl; 
MatrixXd mat2(size, size);
mat2.topLeftCorner(size/2, size/2).setZero();
mat2.topRightCorner(size/2, size/2).setIdentity();
mat2.bottomLeftCorner(size/2, size/2).setIdentity();
mat2.bottomRightCorner(size/2, size/2).setZero();
std::cout << mat2 << std::endl << std::endl; 
MatrixXd mat3(size, size);
mat3 << MatrixXd::Zero(size/2, size/2), MatrixXd::Identity(size/2, size/2), MatrixXd::Identity(size/2, size/2), MatrixXd::Zero(size/2, size/2);
std::cout << mat3 << std::endl; 
输出结果：
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0

0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0

0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0

3、用作临时对象

可以在声明时或在赋值运算符的右侧使用静态方法Zero()和Constant()来初始化变量。可以将这些方法视为返回矩阵或数组。它们返回所谓的表达式对象，这些表达式对象在需要时求值到矩阵或数组，因此该语法不会产生任何开销。这些表达式也可以用作临时对象。
例：

#include 
#include  
using namespace Eigen;
using namespace std; 
int main()
{  
MatrixXd m = MatrixXd::Random(3,3);  
m = (m + MatrixXd::Constant(3,3,1.2)) * 50;  
cout << "m =" << endl << m << endl;  
VectorXd v(3);  
v << 1, 2, 3;  
cout << "m * v =" << endl << m * v << endl;
} 
输出结果：
m =  
10 55.9 14.7
23.2 63.3 77.9
85.6 31.9 77.9
m * v =
166
383
383

该表达式构造所有系数等于1.2加上相应的m系数的3-by-3矩阵表达式：
m + MatrixXf::Constant(3,3,1.2)。

逗号初始化程序也可以用于构造临时对象。下面的示例构造一个大小为2×3的随机矩阵，又乘以(0,1,1,0)矩阵。
例：

MatrixXf mat = MatrixXf::Random(2, 3);
std::cout << mat << std::endl << std::endl;
mat = (MatrixXf(2,2) << 0, 1, 1, 0).finished() * mat;
std::cout << mat << std::endl;
运行结果： 
-1 0.511 0.0655 
-0.737 -0.0827 -0.562 

-0.737 -0.0827 -0.562     
-1 0.511 0.0655

一旦临时子矩阵的逗号初始化完成，此处的finish()方法对于获取实际的矩阵对象是必要的。

如果想更多的深入了解Eigen库，建议花费点时间研究官方文档。