《OpenGL超级宝典（第5版）》——第1章，第1.4节3D编程的基本原则

本节书摘来自异步社区《OpenGL超级宝典（第5版）》一书中的第1章，第1.4节3D编程的基本原则，作者 【美】Richard S. Wright , Jr.Nicholas Haemel，更多章节内容可以访问云栖社区“异步社区”公众号查看

1.4　3D编程的基本原则
现在，我们对实时3D的基本概念已经有了相当程度的认识。我们讨论了一些术语以及PC上的一些示例应用程序。那么，如何在自己的计算机上创建这样的图像呢？好吧，这正是本书剩余部分的任务所在。不过，读者还需要知道一些基础知识，这正是我们接下来将要讨论的。

1.4.1　并非工具包
OpenGL基本上是一种底层渲染API（应用程序接口）。我们不能告诉它“在什么地方绘制什么”——我们需要自己动手，通过载入三角形，应用必要的变换和正确的纹理、着色器并在必要时应用混合模式来组合一个模型。这使我们能够进行大量的底层控制。与使用高层工具包相比，使用OpenGL这样的底层API的动人之处在于，我们不能仅仅是重现许许多多的标准3D渲染算法，我们可以创造自己的算法，甚至可以发现一些新的捷径、性能技巧和艺术视觉技术。

1.4.2　 坐标系统
现在，让我们考虑如何在三维中对物体进行描述。在指定一个物体的位置和大小之前，需要一个参考帧对它进行测量和定位。当我们在一个简单的平面计算机屏幕上绘制点和线时，我们根据行和列指定一个位置。例如，标准的VGA屏幕从左向右为640个像素，自上而下为480个像素。为了在屏幕的中间指定一个位置，可以指定（320，240）的点，也就是距离屏幕左边320个像素、距离屏幕顶端240个像素的位置。
在OpenGL或几乎所有的3D API中创建一个用于绘图的窗口时，必须指定希望使用的坐标系统以及指定的坐标如何映射到实际的屏幕像素。首先，我们讨论在二维绘图中应该怎样做，然后把这个原则扩展到三维图形中。
2D笛卡尔坐标
在二维绘图中，最为常用的坐标系统是笛卡尔坐标系统。笛卡尔坐标由一个x坐标和一个y坐标构成。x坐标测量水平方向的位置，而y坐标则测量垂直方向的位置。
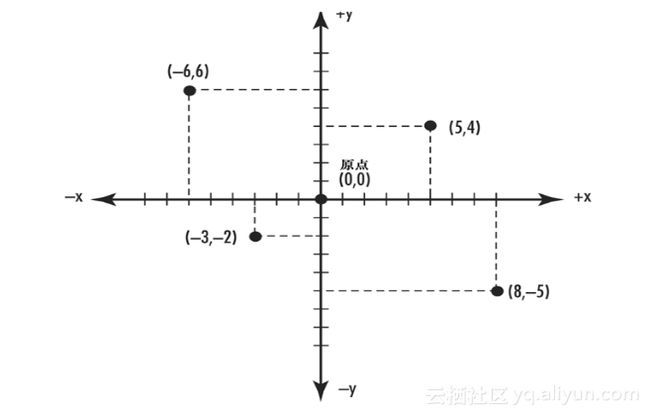
笛卡尔坐标系统的原点（Origin）是（x=0，y=0）。笛卡尔坐标用括号内的一个坐标对来表示，第一个是x坐标，第二个是y坐标，中间由一个逗号分隔。例如，原点就写成（0，0）。图1.17所示描述了二维的笛卡尔坐标系统。带刻度的x和y线被称为“轴”，可以从负无穷延伸到正无穷。这张图是我们在学校时经常使用的真实笛卡尔坐标系统。今天，当我们在绘图时指定坐标系统，不同的窗口映射模式可能会导致坐标的解释不一致。在本书后面章节，我们将看到如何使用不同的方式把真实的坐标空间映射到窗口坐标。

x轴和y轴是垂直的（直角相交），它们共同定义了一个xy平面。简而言之，平面就是指一个扁平的表面。在任何坐标系统中，两条轴（或两条线）如果以直角相交，那么它们就定义了一个平面。很显然，如果一个系统只有两个轴，那么就只有一个平面可以用来绘图。

图1.17　笛卡尔平面
坐标裁剪
窗口是以像素为单位进行度量的。开始在窗口中绘制点、线和形状之前，必须告诉OpenGL如何把指定的坐标对翻译为屏幕坐标。我们可以通过指定占据窗口的笛卡尔空间区域完成这个任务，这个区域称为裁剪区域。在二维空间中，裁剪区域就是窗口内部最小和最大的x和y值。另一种方法是根据窗口指定原点的位置。图1.22所示显示了两种常见的裁剪区域。

图1.18　两个裁剪区域
在第一个例子中，也就是图1.18所示的左侧，窗口x坐标的范围自左向右为0到+150，y坐标的范围从上而下为0到+100，屏幕正中的点用（75，50）来表示。在第二个例子所示的裁剪区域中，x坐标的范围自左向右为-75到+75，y坐标的范围从上而下为-50到+50。在这个例子中，屏幕正中的点就是原点（0，0）。我们还可以使用OpenGL函数（或用于GDI绘图的普通Windows函数）上下反转或左右反转坐标系统。事实上，在Windows窗口的默认映射中，坐标y的值始终为正，并且从上而下递增。这种默认的映射模式在自上而下绘制文本时非常有用，但在绘制图形时则显得不太方便。

视口：把绘图坐标映射到窗口坐标
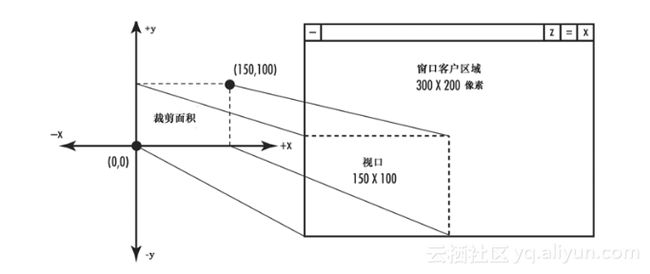
裁剪区域的宽度和高度很少正好与窗口的宽度和高度（以像素为单位）相匹配。因此，坐标系统必须从逻辑笛卡儿坐标映射到物理屏幕像素坐标。这个映射是通过一种叫做视口（ViewPort）的设置来指定的。视口就是窗口内部用于绘制裁剪区域的客户区域。视口简单地把裁剪区域映射到窗口中的一个区域。通常，视口被定义为整个窗口，但这并非严格必须的。例如，我们可能只希望在窗口的下半部分进行绘图。

图1.19所示是个很大的窗口，其大小为300×200像素，它的视口被定义为整个用户区域。如果这个窗口的裁剪区域被设置为沿x轴0至150，沿y轴0至100，我们所看到这个窗口的逻辑坐标将被映射到一个更大的屏幕坐标系统中。逻辑坐标系统的每个增量将与窗口物理坐标系统（像素）的两个增量相匹配。

图1.19　视口被定义为裁剪区域大小的两倍
与此形成对照的是，图1.20所示显示了一个与裁剪区域相匹配的视口。我们所看到的这个窗口仍然是300×200像素。但是，现在可视区域将占据窗口的左下部分。

我们可以使用视口来缩小或放大窗口中的图像，也可以通过把视口设置为大于窗口的用户区域，从而只显示裁剪区域的一部分。

图1.20　视口被定义为与裁剪区域相同的大小
顶点——空间中的一个位置
在2D和3D中，当我们绘制一个物体时，实际上都是用一些更小的称为图元（Primitives）的形状来组成这个物体。图元是一维或二维的实体或表面，如点、直线和多边形（平面多边的形状）。在3D空间中，我们把图元组合在一起创建3D物体。例如一个三维立方体是由6个二维的正方形组成，每个正方形代表一个独立的面。正方形（或其他任何图元）的每个角称为顶点（Vertex）。这些顶点就在3D空间中指定了一个特定的坐标。顶点其实也就是2D或3D空间中的一个坐标。创建实体3D几何图形其实不过就是一种连线游戏罢了。我们将在第3章讨论所有的OpenGL图元以及如何使用它们。
3D笛卡尔坐标
现在，我们把二维坐标系统扩展到三维空间中，并增加深度分量。图1.21所示的笛卡尔坐标系统增加了一个新的轴：z轴。z轴同时垂直于x轴和y轴。它代表了一条从屏幕的中心朝向读者的直线（我们已经旋转了这个坐标系统的视角，把y轴向左旋转，把x轴向下和后旋转。否则，z轴将直接面向我们，无法看到）。现在，我们用3个坐标（x，y，z）来指定三维空间中的一个位置。例如，图1.21所示显示了一个点（-4，4，4）。

图1.21　三维笛卡尔坐标

1.4.3　投影：从3D到2D
我们已经知道如何在3D空间中使用笛卡尔坐标来表示位置。但是，不管我们觉得自己的眼睛所看到的三维图像有多么真实，屏幕上的像素实际上只是二维的。那么OpenGL是如何把这些笛卡尔坐标翻译为可以在屏幕上绘图的二维坐标呢？简而言之，答案就是“三角法和简单的矩阵操纵”。简单？事实上或许并非如此，但是如果我们花很长的篇幅来讨论其中的概念，我们很可能会失去很多对这些细节不感兴趣的读者。而且，如果读者已经忘了大学里所学习的线性代数，那么他们可能无法理解这种“简单”的技巧。在第4章，我们将对此稍作讨论。至于更深入的讨论，读者可以参考附录A“更多阅读建议”中的参考部分。幸运的是，当我们使用OpenGL创建图形时，并不需要对数学有深入的理解。但是，我们在这方面的造诣越深，能够利用OpenGL所发挥的威力也就越大。
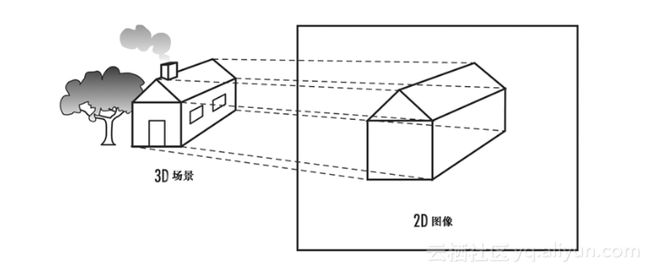
我们真正需要理解的第一个概念称为投影（Projection）。用于创建几何图形的3D坐标将投影到一个2D表面（窗口背景）。这有点像在一块玻璃后面用一支黑色的笔描绘一些物体的外形。当物体消失或者移动玻璃时，我们仍然可以看到这个边缘带角的物体的外形，在图1.22中，背景中的一座房子被描绘到一块扁平的玻璃上。通过指定投影，我们可以指定在窗口中显示的视景体（Viewing Volume），并指定如何对它进行变换。

图1.22　3D图像投影到2D表面
正投影
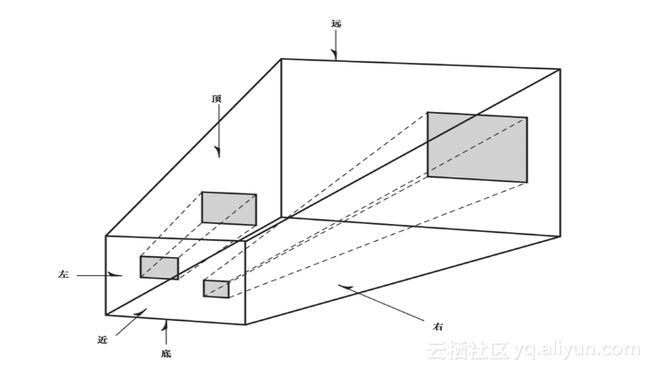
在OpenGL中，绝大多数情况下，我们所关心的是两种主要类型的投影。第一种称为正投影（Orthographic Projection）或平行投影。使用这种投影时，需要指定一个正方形或长方形的视景体。视景体之外的任何物体都不会被绘制。而且，所有实际大小相同的物体在屏幕上都具有相同的大小，不管它们是远是近。这种类型的投影（如图1.23所示）最常用于建筑设计、计算机辅助设计或2D图形中。此外，在3D图形场景中，我们也常常需要使用正投影，在场景的顶部添加文本或者2D覆盖图。

图1.23　正投影的视景体
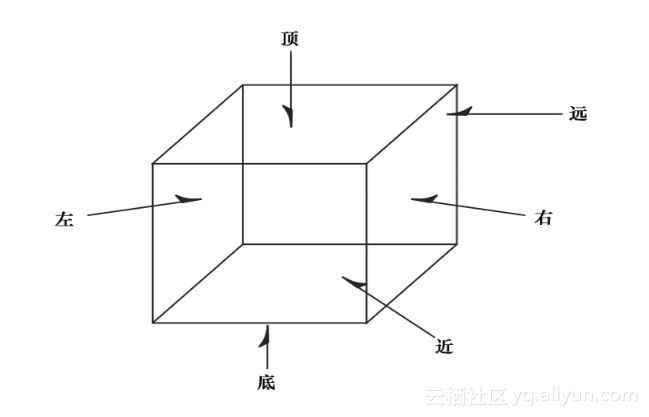
我们还可以在正投影中通过指定远、近、左、右、顶和底裁剪平面来指定视景体。在这个视景体中出现的物体和图形将被投影（考虑它们的方向）到一个在屏幕上出现的2D图像。

透视投影
第二种投影是透视投影（Perspective Projection），它更为常见。在这种投影中，远处的物体看上去比近处的物体更小一些。它的视景体（如图1.24所示）看上去有点像一个顶部被削平的金字塔。剩下来的这个形状称为平截头体（Frustum）。靠近视景体前面的物体看上去比较接近它们的原始大小。但是，当靠近视景体后部的物体被投影到视景体的前部时，它们看上去就显得比较小。在模拟和3D动画中，这种投影能够获得最大程度的逼真感。

图1.24　透视投影的视景体（平截头体）