GIOU、DIOU、CIOU

1 GIOU

论文：https://arxiv.org/abs/1902.09630
代码：https://github.com/generalized-iou/g-darknet

1.1 摘要

IOU是目标检测中的度量标准，但进行目标位置回归时一般使用的是$L_1$或$L_2$损失，作者证明了最小化这些损失并不等同于可以最大化IOU。因此，作者认为应该将最终的优化目标作为损失函数。但是普通的IOU在两个目标框不重叠时值为0，如果以它为损失函数此时反传的梯度为0，无法进行模型的训练。所以作者提出了一个新的度量标准GIOU(generalized IOU)，既把它当做度量标准，又把它当做优化的目标函数。实验结果证明，使用GIOU，在VOC和COCO数据集上取得了更好的目标检测效果。

1.2 简介

IOU，是最常用的用于度量两个任意形状相似度的度量标准。在目标检测中，一般认为通过最小化预测框和真实框之间的$L_n$范数可以最大化预测框和真实框之间的IOU。但实际上并不是这样的。如下图所示：

绿框表示gt box，黑框表示预测框。Fig.1 (a)中，在某一个给定的$l_2$范数时，预测框的右上角的位置在以绿框右上角位置为圆心的、半径为给定的$l_2$范数值的圆上的任一处都是可以的。但是预测框在不同的位置时，预测框和真实框之间的IOU却是存在变化的。Fig. 1(b)中，使用$L_1$范数时，也有相同的结论。因此，证明了使用$L_n$范数作为优化目标并不等同于最大化IOU。$L_n$范数的另一特点是随着检测框的尺度变化而变化，但IOU却具有尺度不变性。

作者提出直接使用IOU作为优化目标，但是IOU在两个目标完全不重叠时值为0，此时虽然偏差很大，但进行反传时的梯度为0，无法进行有效的模型训练。因此作者提出了一个GIOU，在保持IOU优点的同时克服了其缺点，从而使用其取得了更好的目标检测效果。

1.3 GIOU

IOU可以作为距离度量，$L_{IOU}=1-IOU$，其满足度量的四个标准：非负性、对称性、同一性及三角不等式。IOU具有尺度不变性。

IOU的主要缺点是，如果A和B的交集为空，无法度量A和B是离得很近还是离得非常远。

作者提出了GIOU：

C是A和B的最小凸包。

GIOU具有下述性质：

• GIOU也是一个度量，$L_{GIOU}=1-GIOU$，满足非负性、同一性、对称性和三角不等式；
• GIOU具有尺度不变性；
• GIOU是IOU的下限，A和B越一致，GIOU越接近IOU；
• $0\le IOU\le 1$，但$-1\le GIOU\le 1$。在A和B完全重叠时，GIOU等于1；当A和B相距非常远时，GIOU接近于-1。

A和B完全不重叠时，IOU为0，但如果两者离得越远，GIOU就越小，克服了IOU作为损失函数时的缺点。那么最小化$L_{GIOU}$就等价于迫使预测框接近于真实框，从而提高了预测的准确度。

def Giou(rec1,rec2):
    #分别是第一个矩形左右上下的坐标
    x1,x2,y1,y2 = rec1 
    x3,x4,y3,y4 = rec2
    iou = Iou(rec1,rec2)
    area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
    area_1 = (x2-x1)*(y1-y2)
    area_2 = (x4-x3)*(y3-y4)
    sum_area = area_1 + area_2

    w1 = x2 - x1   #第一个矩形的宽
    w2 = x4 - x3   #第二个矩形的宽
    h1 = y1 - y2
    h2 = y3 - y4
    W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)    #交叉部分的宽
    H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)    #交叉部分的高
    Area = W*H    #交叉的面积
    add_area = sum_area - Area    #两矩形并集的面积

    end_area = (area_C - add_area)/area_C    #闭包区域中不属于两个框的区域占闭包区域的比重
    giou = iou - end_area
    return giou

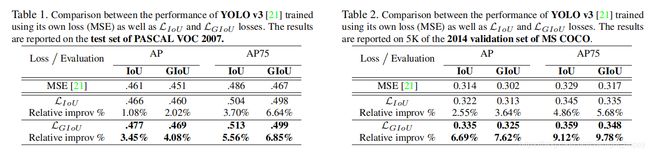
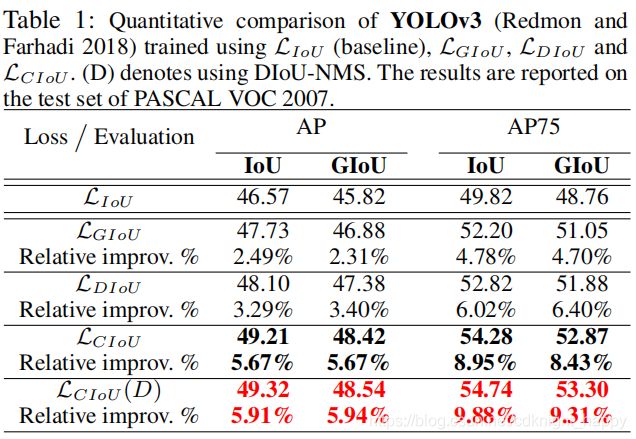
1.4 实验结果

2 DIOU & CIOU

论文：https://arxiv.org/pdf/1911.08287.pdf
代码：https://github.com/Zzh-tju/DIoU

2.1 IOU和GIOU的缺点

DIOU和CIOU是对GIOU的改善，作者首先分析了IOU和GIOU loss的缺点如下。

作者设计了一个包含不同距离、不同尺度和不同宽高比的检测数据集进行仿真实验：

• 在(10,10)点处设置了长宽比分别为1:4,1:3,1:2,1:1,2:1,3:1,4:1的、大小均为1的7个gt box；
• 对于anchor box，作者设计了7种宽高比，分别为1:4,1:3,1:2,1:1,2:1,3:1,4:1；anchor box有7个尺度；anchor box分布在距离(10,10)点半径为3的圆内的5000个点；

整体分布如下图(a)所示，共进行7 * 7 * 7 * 5000 = 1715000次回归。

回归训练的迭代过程为：

$B_i^{t-1}$表示第t-1轮迭代后的预测框的位置；$\nabla B_i^{t-1}$表示第t-1轮迭代后的损失对预测框给位置的梯度；$\eta$表示学习率；$B_i^t$表示第t轮迭代后的预测框的位置；$(2-IO{U}_i^{t-1})$是一个系数，目的是为了加速训练过程。使用$L_1$范数作为bounding box回归的度量标准。

Fig. 3(b)给出了使用不同损失函数时回归的收敛速度，可以明确看出作者提出的DIOU、CIOU的收敛速度快于IOU和GIOU。

Fig. 4是使用不同损失函数经过T轮迭代后的5000个点处的anchor box的回归误差。

Fig. 4(a)看出，IOU loss只对和gt box有重叠的anchor box有效，这是因为当anchor box和gt box不存在重叠时，IOU损失始终为1，无法给出迭代方向。

Fig. 4(b)看出，GIOU loss可以对和gt box不重叠的anchor box起作用，GIOU loss训练完成后的波形的谷底面积大于Fig. 4(a)，证明了相比于IOU loss，GIOU loss的有效性。但是在该图中也可以看出，和(10,10)点水平和垂直位置处的回归误差仍然很大，这是因为GIOU loss的目的是最小化$|C-A\cup B|$，但是当两个框存在包含关系或处于一条线上时，$|C-A\cup B|$比较小甚至可以为0，此时GIOU loss退化成IOU loss。只要训练的时间足够长，GIOU loss是可以取得较好的回归结果的，但是其收敛速度很慢。从Fig. 1可以看出，GIOU loss的训练过程往往是先增大预测框，使其和gt box存在重叠之后，然后再基于IOU使得预测框和真实框的IOU慢慢增大，整体上的收敛速度很慢。
综上，IOU loss无法处理预测框和真实框不交叉的情况，GIOU loss收敛速度慢。因此，作者提出了两个问题：

• 第一，是否应该最小化预测框和真实框中心点之间的距离以加速收敛？
• 第二，当预测框和真实框存在重叠甚至存在包含关系时，如果进行高效准确的回归训练？

2.2 DIOU

基于IOU的损失可以表示为：

$R(B,B^{gt})$表示预测框和真实框之间的惩罚项。

基于作者提出的第一个问题，作者提出了DIOU，即Distance-IOU。使用的惩罚项为预测框和真实框中心点之间的欧式距离除以两个框闭包框的对角线长度的平方。即：

因此，总的D-IOU损失为：

如Fig.5所示，D-IOU目的是最小化预测框和真实框中心点之间的距离，而GIOU目的是最小化$C-B\cup B^{gt}$。

相比于IOU和GIOU，DIOU和它们具有下述相同点：

• DIOU仍然具有尺度不变性；
• 在预测框和真实框不重叠时，DIOU向GIOU一样可以进行训练；
• 当预测框和真实框重叠时，IOU损失、GIOU损失和DIOU损失均为0，当两个框远离时，GIOU损失和DIOU损失接近于2.

但DIOU损失相比于IOU损失和GIOU损失，又具有下列优点：

• DIOU损失直接优化两个框中心点间的距离，比GIOU收敛更快；
• 当预测框和真实框存在包含关系时，或者是在一条线上时，DIOU损失仍然可以快速迭代，但此时GIOU由于$C-A\cup B$趋于0而退化为IOU损失。

def Diou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    dious = torch.zeros((rows, cols))
    if rows * cols == 0:#
        return dious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        dious = torch.zeros((cols, rows))
        exchange = True
    # #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1] 
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]
    
    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2 
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2 
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:]) 
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2]) 
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:]) 
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    dious = inter_area / union - (inter_diag) / outer_diag
    dious = torch.clamp(dious,min=-1.0,max = 1.0)
    if exchange:
        dious = dious.T
    return dious

2.3 CIOU

CIOU对应于作者提出的第二个问题，一个好的损失函数不仅应该考虑中心点的距离，而且应该考虑两个框的重叠面积和宽高比等因素。IOU loss考虑了重叠面积、DIOU增加了中心点距离，另一个CIOU又考虑了两个框的长宽比。

v对于w和h的梯度为：

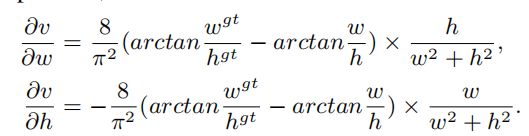
由于w和h进行了归一化处理，因此$w^2+h^2$比较小，所以会发生梯度爆炸。因此作者在实现的时候移除了这个分母，这样并不会改变梯度的方向。

def bbox_overlaps_ciou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    cious = torch.zeros((rows, cols))
    if rows * cols == 0:
        return cious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        cious = torch.zeros((cols, rows))
        exchange = True

    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1]
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]

    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    u = (inter_diag) / outer_diag
    iou = inter_area / union
    with torch.no_grad():
        arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)
        v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
        S = 1 - iou
        alpha = v / (S + v)
        w_temp = 2 * w1
    ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)
    cious = iou - (u + alpha * ar)
    cious = torch.clamp(cious,min=-1.0,max = 1.0)
    if exchange:
        cious = cious.T
    return cious

2.4 结合DIOU进行NMS

NMS最大的问题是容易在密集目标检测中因为不同目标靠的太近而被误删。作者将DIOU应用到NMS过程中，因为DIOU考虑了两个框中心点的距离。

DIOU-NMS：

两个框IOU很大，中心点的距离也很大，那么有可能是两个不同的目标，保持暂时先不删。

2.5 实验结果

参考：https://zhuanlan.zhihu.com/p/94799295?from_voters_page=true