【多目标跟踪学习笔记】1.卡尔曼滤波(Kalman Filter)
零 前言
在有些场景中,我们希望通过来自不同方面的数据来预测系统的下一个状态。卡尔曼滤波是解决此类问题的一个算法,但是其只能应用于线性的高斯系统。
\space
\space
一 引言
通过一个简单的例子先来说明。假如我们想预测一辆车下一时刻的位置,我们有两大数据来源:一是IMU(Internal Measurement Unit,可以测量加速度、角速度等),二是GPS,三是速度表。结合这三个测量值,我们可以估算出汽车的位置。卡尔曼滤波就可以应用于这个场景。
卡尔曼滤波总体的两大用处:
- 可以优化估算一些无法直接测量但可以间接测量的量
- 可以结合多个传感器的信息来估测系统现在的状态
\space
\space
二 从状态观测器的角度理解卡尔曼滤波
先写一下控制理论里面的几个简单概念:
- 状态变量: 确定系统状态的一组独立(最小)变量。是能完整、确定地描述系统的时域行为的最少的一组变量。
- 状态方程: 描述系统的状态变量之间,及其和系统输入量之间关系的一阶微分方程组。
- 输出方程: 描述系统输出变量与状态变量(有时还包括输入变量)之间的函数关系的代数方程。
- 状态观测器: 为了实现状态反馈控制,就要设法利用巳知的信息(输入量及输出量),通过一个模型来对状态变量进行估计。
系统的状态空间表达式由状态方程和输出方程组成,一般可以表示为:
x ˙ = A x + B u y = C x \dot{x}=Ax+Bu \\ y=Cx x˙=Ax+Buy=Cx
我们设计一个状态观测器 (在问题中,就是我们建立的模型) 来估计系统状态,状态观测器的系统状态变量和输出都用字母加hat表示,其状态空间表达式为:
x ^ ˙ = A x ^ + B u y ^ = C x ^ \dot{\hat{x}}=A\hat{x}+Bu \\ \hat{y}=C\hat{x} x^˙=Ax^+Buy^=Cx^
系统框图如下:

蓝色部分就是state observer,K是负反馈系统,用于将误差 x − x ^ x-\hat{x} x−x^最小化。
误差的表达式为:
e o b s = x − x ^ e_{obs}=x-\hat{x} eobs=x−x^
由:
x ˙ = A x + B u x ^ ˙ = A x ^ + B u + K ( y − y ^ ) \dot{x}=Ax+Bu \\ \dot{\hat{x}}=A\hat{x}+Bu + K(y-\hat{y}) x˙=Ax+Bux^˙=Ax^+Bu+K(y−y^)
得到:
e o b s ˙ = x ˙ − x ^ ˙ = A ( x − x ^ ) − K ( C ( x − x ^ ) ) = A e o b s − K C e o b s = ( A − K C ) e o b s \dot{e_{obs}}=\dot{x}-\dot{\hat{x}}=A(x-\hat{x})-K(C(x-\hat{x}))=Ae_{obs}-KCe_{obs}=(A-KC)e_{obs} eobs˙=x˙−x^˙=A(x−x^)−K(C(x−x^))=Aeobs−KCeobs=(A−KC)eobs
解这个微分方程,得到:
e o b s ( t ) = e ( A − K C ) t e o b s ( 0 ) e_{obs}(t)=e^{(A-KC)t}e_{obs}(0) eobs(t)=e(A−KC)teobs(0)
所以,如果 A − K C < 0 A-KC<0 A−KC<0,则误差会收敛,否则不会。 因此 K K K的选择对于收敛速度就尤为重要,选择 K K K的方法,就是使用Kalman滤波器。
\space
\space
三 卡尔曼滤波的工作原理
先以一个最简单的一维例子说明。假设我们要造一个自动驾驶汽车,而且想要时刻预测它的位置。那么状态向量就只有位置信息一个,即 k k k时刻的状态为:
x k = [ p o s i t i o n ] x_k=[position] xk=[position]
我们要获取的信息就是小车的位置,因此
y k = C x k = x k y_k=Cx_k=x_k yk=Cxk=xk
假设系统的输入是速度,考虑噪声(干扰),其框图可表示如下:

其中 A A A为状态转换矩阵,将上一状态投射到这一状态; B B B为控制输入矩阵,将输入投射到当前状态; v k ∼ N ( 0 , R ) , w k ∼ N ( 0 , Q ) v_k\sim N(0,R), w_k\sim N(0,Q) vk∼N(0,R),wk∼N(0,Q).(卡尔曼滤波适用于线性、高斯)
这时候,跟之前说的模型一样,我们有一个自己计算小车位置的模型。此时卡尔曼滤波的作用就是将我们模型的预测值和测量值结合起来,得到最佳的新的状态的估计。 如下图所示:

- 好像跟前面第二部分 K K K的作用有些出入,不过Kalman的确是“作用”在真实测量和模型预测之间,来减少误差的部分。所以Kalman滤波的确像一个状态观测器,只不过它是针对随机系统的。
具体怎么做呢?假设 k − 1 k-1 k−1时刻小车的状态为 x k − 1 x_{k-1} xk−1,其是一个高斯分布。第 k k k时刻状态为 x k x_k xk,且方差会增加(为什么?),测量值也是高斯分布,我们将这两个高斯分布相乘,就能得到最佳估计值,如下图所示:
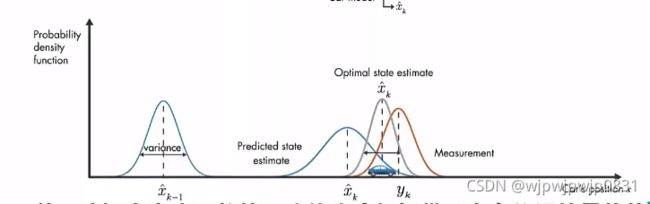
这就是一维case的基本思想。
我手推了一下(懒得打公式了),思路参考的是卡尔曼滤波:从入门到精通,知乎专栏


因此,卡尔曼滤波就是一个将预测和测量结合,进行数据融合的算法,如此进行迭代下去,就可以预测每一时刻的状态。
再总结一下,Kalman滤波分两步,
1.predict:
x t ^ − = A x t − 1 ^ + B u t P t − = A P t − 1 A T + Q \hat{x_t}^-=A\hat{x_{t-1}}+Bu_t \\ P_t^-=AP_{t-1}A^T+Q xt^−=Axt−1^+ButPt−=APt−1AT+Q
2.update:
K t = C t P t − C t P t − C t T + R , 称 作 卡 尔 曼 增 益 x t ^ = x t ^ − + K t ( y t − C t x t ^ − ) P t = ( I − K t C t ) P t − K_t=\frac{C_tP_t^-}{C_tP_t^-C_t^T+R} ,称作卡尔曼增益\\ \hat{x_t}=\hat{x_t}^-+K_t(y_t-C_t\hat{x_t}^-) \\ P_t=(I-K_tC_t)P_t^- Kt=CtPt−CtT+RCtPt−,称作卡尔曼增益xt^=xt^−+Kt(yt−Ctxt^−)Pt=(I−KtCt)Pt−
可以看到,状态更新方程 x t ^ = x t ^ − + K t ( y t − C t x t ^ − ) \hat{x_t}=\hat{x_t}^-+K_t(y_t-C_t\hat{x_t}^-) xt^=xt^−+Kt(yt−Ctxt^−)很像状态观测器方程,再次说明了卡尔曼滤波就是一种特殊的state observer。
\space
注
卡尔曼滤波只适用于线性高斯分布情形,对于其他情形有扩展卡尔曼滤波、粒子滤波等。以后再学,把他们的特点和使用条件先记一下。


