c++十大经典排序算法

目录

代码

1 冒泡排序

2. 选择排序

3. 插入排序

4. 希尔排序

5. 归并排序

6. 快速排序

7. 堆排序

8. 计数排序

9. 桶排序

10. 基数排序

总结

技术参考

---

代码

1 冒泡排序

冒泡排序是一种简单直观的入门排序算法。它的原理就是从第一个元素开始，与后面的元素逐个比较，如果顺序不对就交换，直到没有可比较的元素为止。

 1 // 冒泡排序
 2 void BublingSort(int *arr, int len)
 3 {
 4     if(len == 0)
 5     {
 6         return;
 7     }
 8     std::cout<<"冒泡排序"< arr[j])
14             {
15                 std::swap(arr[i], arr[j]);
16             }
17         }
18     }
19 }

 冒泡排序是稳定的排序，思路简单和代码都非常简单，但是算法复杂度较高，不适合大数据量场景使用。

2. 选择排序

选择排序是基于冒泡排序的优化，减少了交换的次数。每次遍历后找出最小/最大的元素，然后和第一个元素交换，再从剩下的元素里重复这个过程。

 1 void SelectSort(int *arr, int length)
 2 {
 3     std::cout<<"选择排序"<< std::endl;
 4     for(int i = 0; i < length; ++i)
 5     {
 6         int min_pos = i;
 7         for(int j = i +1; j < length; ++j)
 8         {
 9             if(arr[min_pos] > arr[j])
10             {
11                 min_pos = j;
12             }
13         }
14         if(min_pos != i)
15         {
16             int tmp = arr[i];
17             arr[i] = arr[min_pos];
18             arr[min_pos] = tmp;
19         }
20     }
21 }

用数组实现的选择排序是不稳定的。用链表结构则是稳定的。

选择排序优于冒泡排序，但同样不适合在大数据量场景使用。

3. 插入排序

原理是把第一个元素当做已经排好序的队列，从第二个元素开始依次比较已经排好序的队列，找到合适的位置进行交换。这和我们平时打扑克牌摸牌的过程差不多。

 1 void InsertSort(int *arr, int len)
 2 {
 3     if(len == 0)
 4     {
 5         return;
 6     }
 7 
 8     std::cout<<"插入排序"< 0)
14         {
15             if(arr[j - 1] > arr[j])
16             {
17                 std::swap(arr[j], arr[j-1]);
18             }
19             --j;
20         }
21     }
22 }

 插入排序是稳定的算法，但是不适合大数据量场景中使用。

4. 希尔排序

尔排序是基于插入排序的一种改进。

希尔排序（shell sort）这个排序方法又称为缩小增量排序，是1959年D·L·Shell提出来的。该方法的基本思想是：设待排序元素序列有n个元素，首先取一个整数increment（小于n）作为间隔将全部元素分为increment个子序列，所有距离为increment的元素放在同一个子序列中，在每一个子序列中分别实行直接插入排序。然后缩小间隔increment，重复上述子序列划分和排序工作。直到最后取increment=1，将所有元素放在同一个子序列中排序为止。

 1 void ShellSort(int *arr, int length)
 2 {
 3     std::cout<<"希尔排序"< 0; gap /=2)
 5     {
 6         for(int i = gap; i < length; ++i)
 7         {
 8             int j = i;
 9             while((j - gap) >= 0 && arr[j] < arr[j - gap])
10             {
11                 int tmp = arr[j-gap];
12                 arr[j-gap] = arr[j];
13                 arr[j] = tmp;
14                 j -= gap;
15             }
16         }
17     }
18 }

 希尔排序优于插入排序，适用于中小规模数据量场景。

5. 归并排序

归并排序是用分治的思想处理，通过递归不断将数组分割为两部分，直到最小单元只有1个元素，然后对两两最小单元进行比较合并。

 1 void MergeArr(int *arr, int left, int mid, int right)
 2 {
 3     // 设置两个游标
 4     int curLeft = left;
 5     int curMid = mid;
 6     // 开辟一个缓存区
 7     int len = right - left + 1;
 8     int *tmpArr = new int[len];
 9     // 从两个序列依次取出按顺序放入缓存区
10     int *curArr = tmpArr;
11     while(curLeft < mid && curMid <= right) // 注意mid是右边序列的第一个元素位置 不能用等号判断
12     {
13         if(arr[curLeft] <= arr[curMid])
14         {
15             *curArr++ = arr[curLeft++];
16         }
17         else
18         {
19             *curArr++ = arr[curMid++];
20         }
21     }
22     while(curLeft < mid)
23     {
24         *curArr++ = arr[curLeft++];
25     }
26     while(curMid <= right)
27     {
28         *curArr++ = arr[curMid++];
29     }
30 
31     for(int i = left, k = 0; i <= right;)
32     {
33         arr[i++] = tmpArr[k++];
34     }
35 
36     delete[] tmpArr;
37 }
38 
39 void MergeSort(int *arr, int left, int right)
40 {
41     if(left >= right)
42     {
43         return;
44     }
45 
46     int mid = (left + right) >> 1;
47     MergeSort(arr, left, mid);
48     MergeSort(arr, mid + 1, right);
49     MergeArr(arr, left, mid + 1, right);
50 }

归并排序在数据量比较大的时候也有较为出色的表现（效率上），但是，其空间复杂度O(n)使得在数据量特别大的时候（例如，1千万数据）几乎不可接受。而且，考虑到有的机器内存本身就比较小，因此，采用归并排序一定要注意。

6. 快速排序

快速排序和归并排序都是用分治法处理的，归并排序是按长度平均分成子序列最后合并比较。而快速排序一般是以第一个元素作为基准数，分成大于和小于基准数的子序列。

 1 void QuickSort(int *arr, int left, int right)
 2 {
 3     if(left >= right)
 4     {
 5         return;
 6     }
 7 
 8     int cur_left = left;
 9     int cur_right = right;
10     int tmp_value = arr[cur_left];
11 
12     while(cur_left < cur_right)
13     {
14         while(cur_left < cur_right && arr[cur_right] > tmp_value)
15         {
16             --cur_right;
17         }
18         if(cur_left < cur_right)
19         {
20             arr[cur_left++] = arr[cur_right];
21         }
22         while(cur_left < cur_right && arr[cur_left] < tmp_value)
23         {
24             ++cur_left;
25         }
26         if(cur_left < cur_right)
27         {
28             arr[cur_right--] = arr[cur_left];
29         }
30     }
31 
32     arr[cur_left] = tmp_value; // 每次递归都确定了一个正确的位置
33     QuickSort(arr, left, cur_left - 1);
34     QuickSort(arr, cur_left + 1, right);
35 }

 快排是不稳定的算法，但是在大部分场景都适合使用，尤其是大数据量场景中性能优势明显。

7. 堆排序

二叉堆是一颗完全二叉树，一般用数组表示。其中根元素用 arr[0] 表示，而其他结点（第 i 个结点的存储位置,i > 0）满足下表中的特性：

• 第i个节点的父节点所在的位置: arr[i/2];

• 第i个节点的左孩子:arr[2 * i + 1]:

• 第i个节点的右孩子:arr[2 * i + 2]:

堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。一般升序用大顶堆，降序用小顶堆。

堆排序步骤:

• 用无序数组构建大顶堆;

• 将根节点数据与数组最后一个元素交换值;

• 在除最后一个元素的剩下数组里重构大顶堆;

• 重复上面两个步骤，直到只剩下一个元素即根节点，算法结束。

 1 void HeapAdjust(int *arr, int length, int root)
 2 {
 3     int left_child = root * 2 + 1;
 4     int right_child = root * 2 + 2;
 5 
 6     int max_idx = root;
 7     if(left_child < length && arr[left_child] > arr[max_idx])
 8     {
 9         max_idx = left_child;
10     }
11     if(right_child < length && arr[right_child] > arr[max_idx])
12     {
13         max_idx = right_child;
14     }
15 
16     if(max_idx != root)
17     {
18         int tmp = arr[max_idx];
19         arr[max_idx] = arr[root];
20         arr[root] = tmp;
21         HeapAdjust(arr, length, max_idx);
22     }
23 }
24 
25 void HeapSort(int *arr, int length)
26 {
27     // 构建大顶堆
28     for(int i = length / 2 - 1; i >= 0; --i)
29     {
30         HeapAdjust(arr, length, i);
31     }
32     // 用大顶堆完成升序排序
33     for(int i = length - 1; i > 0; --i)
34     {
35         int tmp = arr[0];
36         arr[0] = arr[i];
37         arr[i] = tmp;
38         HeapAdjust(arr, i, 0);
39     }
40 }

堆排序在建立堆和调整堆的过程中会产生比较大的开销，在元素少的时候并不适用。但是，在元素比较多的情况下，还是不错的一个选择。尤其是在解决诸如“前n大的数”一类问题时，几乎是首选算法。

8. 计数排序

任何比较排序算法的时间复杂度的上限为O(NlogN), 不存在比o(nlgN)更少的比较排序算法。如果想要在时间复杂度上超过O(NlogN)的时间复杂度，肯定需要加入其它条件。计数排序就加入了限制条件，从而使时间复杂度为O(N).

计数排序的核心思想(来自算法导论）：计数排序要求待排序的n个元素的大小在[0, k]之间，并且k与n在一个数量级上，即k=O(n).对于每一个输入元素x, 确定小于等于x的个数为i。利用这一信息，就可以把元素x放到输出数组的正确位置,即把元素x放到输出数组下标为i-1的位置。

代码比较简单:

 1 void CountSort(int *arr, int length, int max_value)
 2 {
 3     if(arr == NULL || length <= 0)
 4     {
 5         return;
 6     }
 7     int *tmp_arr = new int[max_value + 1]();
 8     for(int i = 0; i < length; ++i)
 9     {
10         ++tmp_arr[arr[i]];
11     }
12     int idx = 0;
13     for(int i = 0; i < max_value + 1; ++i)
14     {
15         while (tmp_arr[i] > 0)
16         {
17             arr[idx++] = i;
18             --tmp_arr[i];
19         }
20     }
21 }

 计数排序适用于确定最大值且数据量集中的场景，比如高考分数排序。

9. 桶排序

 桶排序是按一定规则分配n个桶，这n个桶是有序的。然后对桶内的数字再进行排序，最后依次合并桶内数据。

需要注意三个点：

1. 桶的数据结构可以用数组或者链表，用链表更加灵活，没有大小限制

2. 桶的划分规则视具体业务而定，以数据能均匀分布到各个桶内为基准。

3. 单个桶的排序算法不固定，一般用插入排序。

 1 void bucket_sort(int *arr, int len)
 2 {
 3     if(len<= 0)
 4     {
 5         return;
 6     }
 7     cout<<"桶排序"< 0 && temp < buckets[index][j - 1]; --j)
23         {
24             buckets[index][j] = buckets[index][j - 1];
25         }
26         buckets[index][j] = temp;
27     }
28 
29     int k = 0;
30     for(int i = 0; i < 10; ++i)
31     {
32         for(int j = 0; j < count[i]; ++j)
33         {
34             arr[k++] = buckets[i][j];
35         }
36     }
37 
38     for(int i = 0 ; i < 10; ++i)
39     {
40         delete []buckets[i];
41         buckets[i] = NULL;
42     }
43     delete []buckets;
44     buckets = NULL;
45 }

桶排序可用于最大最小值相差较大的数据情况，但桶排序要求数据的分布必须均匀，否则可能导致数据都集中到一个桶中。比如[104,150,123,132,20000], 这种数据会导致前4个数都集中到同一个桶中。导致桶排序失效。

10. 基数排序

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

 1 int GetMaxBits(int *arr, int len)
 2 {
 3     if(len<= 0)
 4     {
 5         return 0;
 6     }
 7     int ret = 0;
 8     for(int i  = 0; i < len; ++i)
 9     {
10         int tmp = arr[i];
11         int k = 0;
12         while(tmp > 0)
13         {
14             tmp /= 10;
15             ++k;
16         }
17         if(k > ret)
18         {
19             ret = k;
20         }
21     }
22 
23     return ret;
24 }
25 
26 void RadixSort(int *arr, int len)
27 {
28     if(len<= 0)
29     {
30         return;
31     }
32     cout<<"基数排序"<= 0; --q)
61         {
62             int tmp = (arr[q] / radix) % 10;
63             tmparr[count_arr[tmp] - 1] = arr[q];
64             count_arr[tmp]--;
65         }
66 
67         for(int i = 0; i < len; ++i)
68         {
69             arr[i] = tmparr[i];
70         }
71 
72         radix *= 10;
73     }
74 
75     
76 
77     delete[] tmparr;
78     delete[] count_arr;
79 }

基数排序要求较高，元素必须是整数，整数时长度10W以上，最大值100W以下效率较好，但是基数排序比其他排序好在可以适用字符串，或者其他需要根据多个条件进行排序的场景，例如日期，先排序日，再排序月，最后排序年 ，其它排序算法可是做不了的。

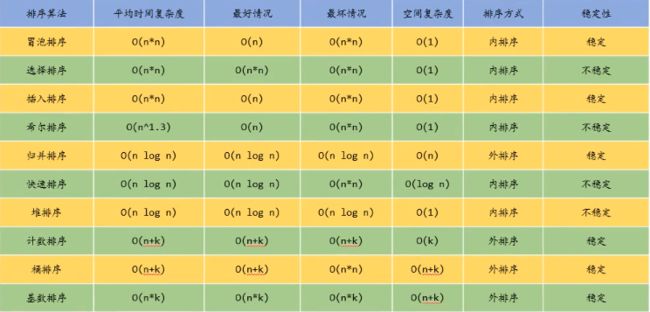
总结

最后附上各种排序的复杂度和稳定性：

技术参考

1. 视频技术参考：C/C++Linux服务器开发/后台架构师