在线学习(online learning)——Chapter 2 Problem Formulations and Related Theory

在线学习(online learning)——Chapter 2 Problem Formulations and Related Theory

本章中，我们将首先给出一个经典的在线学习问题的形式化描述，即在线二分类(online binary classification)，然后介绍统计学习理论、在线凸优化和博弈论的基本知识，作为在线学习技术的理论基础。

一、问题的设立

考虑一个在线二分类任务，在线学习以序列方式进行的。在每一轮中，学习器接收一个数据实例，然后对该实例进行预测。在做出预测后，学习者从环境中获得关于实例的真实答案作为反馈(feedback)。根据反馈，学习者可以根据预测和答案之间的差值(difference)来衡量损失(loss)。最后，学习器通过某种策略(strategy)更新其预测模型，以提高对未来接收实例的预测性能。

将垃圾邮件检测视为在线二分类的运行示例，其中学习者以二分方式回答每个问题: 是或否。该任务是有监督的二分类问题(supervised binary classification)。

我们可以公式化地描述如上问题：

1. 考虑一个用向量空间表示的实例/对象序列，$x_t\in {\mathbb{R}}^d$，其中 $t$ 表示第 $t$ 轮，$d$ 表示维度，使用 $y_t\in \{+1,-1\}$表示实例的标签。
2. 在线二分类任务以序列方式进行，在第 $t$ 轮，学习器收到实例 $x_t$，然 后使用一个二分类器 $w_t$进行预测
3. 比如 ${\hat{y}}_t=\text{sign}(w_t^T{x}^t)$，当$w_t^T{x}^t\ge 0$ 输出 ${\hat{y}}_t=+1$，当$w_t^T{x}^t<0$ 输出 ${\hat{y}}_t=-1$
4. 做出预测后，学习器接收到真实的标签 $y_t$，然后衡量损失，比如使用 $hinge-loss\ell (w_t)=\max (0,1-y_t{w}_t^T{x}^t)$
5. 当损失不为零时，学习者通过在训练示例 $(x_t,y_t)$ 上应用一些策略，将预测模型从 $w_t$ 更新到 $w_{t+1}$。

算法1总结了在线二分类的过程。

通过连续 $T$ 轮进行在线学习，可以衡量在线学习者所犯的错误数量为 $M_T={\sum }_{t=1}^TⅡ(\widehat{y_t}\ne y_t)$。一般来说，在线学习任务的经典目标是尽量减少在线学习者对后知的最佳固定模型的预测的悔值(regret)，定义为
$$R_T=\sum _{t=1}^T{\ell }_t(w_t)-\underset{w}{\min }\sum _{t=1}^T{\ell }_t(w)\text{\hspace{1em}(1)}$$
其中第二项是最优模型 $w^{\ast }$所遭受的损失，只有在看到所有实例及其标签后才能知道。从悔值最小化的理论角度来看，如果一个在线算法保证它的后悔关为 $T$ 的函数是次线性的(sublinear) ，即$R_T=o(T)$，这意味着${\lim }_{T\to \infty }R(T)/T=0$，即平均而言，学习者的表现几乎与最好的固定模型一样好。

二、统计学理论

接下来介绍一些统计学的基本概念和框架。

2.1 经验误差最小化

假设实例$x_t$ 由一个固定但未知的分布 $P(x)$随机生成，它的类标签 $y$ 也由一个固定但未知的分布 $P(y|x)$ 生成。标记数据的联合分布为 $P(x,y)=P(x)P(y|x)$ 。目标是找到一个预测函数 $f(x)$，使损失函数的期望值最小化：
$$R(f)=\int \ell (y,f(x))\text{d}P(x,y)$$
它也被称为 $TrueRisk$ 函数。它的解 $f^{\ast }=\text{arg}\min R(f)$ 是最优的预测器。通常，由于未知分布$P(x,y)$，不能直接计算 $TrueRisk$ 函数 $R(f)$。在实践中，我们通过估计有限的实例集合$(x_1，y_1),\dots ,(x_n，y_n)$得出的$\text{i.i.d}$ 上的风险来近似真实的风险，这称为“经验风险”(Empirical Risk)或“经验误差"(Empirical Error)。
$$R_{emp}(f)=\frac{1}{N}\sum _{n=1}^N\ell (y_n,f(x_n))$$
使用经验误差最小化（Empirical Error Minimization ERM），学习的问题是在一个假设空间$\mathcal{F}$上通过最小化经验误差找到一个假设$f$：
$$\widehat{f_n}=\text{arg}\underset{f\in \mathcal{F}}{\min }{R}_{emp}(f)$$
ERM是许多机器学习算法的理论基础。例如，在二分类问题中，假设$\mathcal{F}$是线性分类器的集合，并使用$hinge-loss$，ERM原理表明，通过最小化以下目标，可以训练出最佳线性模型 $w$：
$$R_{emp}(w)=\frac{1}{N}\sum _{n=1}^N\max (0,1-y_n{w}^T{x}_n)$$

2.2 误差分解

最佳预测因子$f^{\ast }$和经验最佳预测因子$\widehat{f_n}$之间的差异可以通过 $ExcessRisk$ 来衡量，它可以分解如下:

其中第一项被称为估计误差（Estimation Error），因为有限数量的训练样本可能不足以代表未知分布，第二项被称为近似误差（Approximation Error d），因为模型类 $\mathcal{F}$ 的限制可能不够灵活，无法包括最佳预测因子$f^{\ast }$。

一般情况下，增加训练数据量会减小估计误差，而增加模型的复杂度/容量可以减小近似误差。然而，随着模型复杂性的增加，估计误差往往会增加，给模型选择带来挑战。

三、凸优化理论

许多在线学习问题本质上可以(重新)表述为在线凸优化(Online Convex Optimization OCO)任务。下面，我们将介绍OCO的一些基础知识。

在线凸优化任务通常由两个主要元素组成：凸集 $\mathcal{S}$ 和凸代价函数 ${\ell }_t(\cdot )$。在每一个时间步 $t$，在线算法决定选择一个权重向量 $w_t\in \mathcal{S}$，之后基于凸代价函数计算损失 ${\ell }_t(w_t)$。在线算法的目标是选择一个决策序列 $w_1,w2，\dots$，使得悔值最小化。

更正式地说，在线算法的目标是在 $T$ 轮之后实现低悔值 $R_T$，其中悔值 $R_T$被定义为：
$$R_T=\sum _{t=1}^T{\ell }_t(w_t)-\underset{w^{\ast }}{\inf }\sum _{t=1}^T{\ell }_t(w^{\ast })$$

其中$w^{\ast }$是最小化凸目标函数 ${\sum }_{t=1}^T{\ell }_t(w)$ 的解。

inf： infimum 或 infima，中文叫下确界或最大下界。 inf(S)， S表示一个集合， inf(S)是指集合S的下确界， 即小于或等于S中所有元素的最大值， 这个数不一定在集合S中。

例如，考虑一个在线二分类任务，用于从标记实例 $(x_t,y_t),t=1,...,T$ 序列训练在线支持向量机(SVM)，其中$x_t\in {\mathcal{R}}^d,y_t\in \{+1,-1\}$。对于某个常数参数 $C$，可以将损失函数$\ell (\cdot )$定义为${\ell }_t(w_t)=\max (0,1-y_t{w}^{T}x)$，凸集 $\mathcal{S}$ 定义为 $\{\forall w\in {\mathcal{R}}^d|\Vert w\Vert \le C\}$。有多种算法可以解决这个问题。下面我们简要回顾三种主要的在线凸优化方法，包括一阶算法、二阶算法和基于正则化的方法。

3.1 一阶方法

一阶方法旨在利用一阶梯度信息优化目标函数。在线梯度下降(Online Gradient Descent OGD)(Zinkevich, 2003)可以被看作是凸优化中的随机梯度下降(Stochastic Gradient Descent SGD)的在线版本，是最简单和最流行的凸优化方法之一。

在每一次迭代中，算法根据实例 $x_t$ 所遭受的损失，按照当前损失函数梯度的方向，从当前模型更新到新的模型。由更新可知：$u=w_t-{\eta }_t\nabla {\ell }_t(wt)$。由此产生的更新可能会将模型推到可行域(feasible domain)之外。因此，该算法将模型投影到可行域中，即 ${\Pi }_{\mathcal{S}}(u)=\text{arg}\min \Vert w-u\Vert$(其中$\Pi$表示投影操作)。OGD是简单和容易实现的，但投影步骤有时可能是计算密集型的，这取决于特定的任务。理论上(Zinkevich, 2003)，对于(有界梯度的) 凸代价函数的任意序列$T$，OGD实现了次线性悔值$O(\sqrt{T})$。

论文链接

3.2 二阶方法

二阶算法指的是利用模型的二阶信息，如模型的协方差矩阵，样本的相关性矩阵等来构造更新规则。这一类型的算法能加速在线学习算法的收敛速率。

一种流行的方法是 Online Newton Step 算法。Online Newton Step(Hazan 等人， 2007)可以被视为批量优化中Newton-Raphson方法的在线模拟。与OGD一样，ONS也通过在每次在线迭代中从当前模型中减去一个向量来执行更新。

OGD减去的向量是基于当前模型的损失函数的梯度，而ONS减去的向量是逆Hessian矩阵乘以梯度，即 $A_t^{-1}\nabla {\ell }_t(w_t)$，其中 $A_t$ 与 Hessian 矩阵有关。 $A_t$ 也在每次迭代中更新，$A_t=A_{t-1}+\nabla {\ell }_t(w_t)\nabla {\ell }_t(w_t{)}^T$。更新后的模型投影回可行域, $w_{t+1}={\Pi }_{\mathcal{S}}^{A_t}{w}_t-\eta A_t^{-1}\nabla {\ell }_t(w_t)$，其中${\Pi }_{\mathcal{S}}^A=\text{arg}{\min }_{w\in S}(w-u{)}^{T}A(w-u)$。

与OGD在欧几里得范数下进行投影不同，ONS在矩阵 $A_t$ 所诱发的范数下进行投影。虽然ONS的时间复杂度$O(n^2)$高于OGD的 $O(n)$，但在相对较弱的exp-concave代价函数假设下，它保证了对数悔值$O(\log T)$。

论文链接

3.3 正则化

与传统的凸优化不同，OCO的目标是优化悔值。传统的方法(被称为Follow the Leader (FTL))可能不稳定，在最坏的情况下导致高悔值(例如线性悔值)。这激发了通过正则化来稳定这些方法的需求。这里我们介绍常用的正则化方法。

Follow-the-Regularized-Leader (FTRL)

通过对FTL增加一个凸的、光滑的和二次可微分的正则化项 $R(w)$ 来达到优化目的，在每次迭代中解决如下优化问题：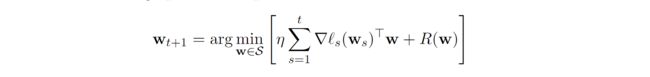

理论上，FTRL算法总体上实现了一个次线性悔值界$O(\sqrt{T})$。

Online Mirror Descent (OMD)

Online Mirror Descent算法是离线优化算法Mirror Descent在在线学习场景中的应用。它是广泛应用的梯度下降方法的一种泛化形式。Online Mirror Descent(OMD)算法有两种形式。算法流程如下从上面算法流程我们可以看出两种更新策略都是通过函数VR进行更新的。OMD算法的泛化能力来源于它的更新策略是在对偶空间进行的，且对偶空间是根据正则项进行定义的。正则项的梯度就像是从 ${\mathbb{R}}^d$ 到它自己的一个映射。Lazy方式更新关注欧式空间下的一个点，并在每轮预测的时候将其投影到定义域上。Active方式更新时刻关注模型本身，它也可以看作是OGD算法的一个泛化。

OMD算法的lay更新和FTRL有一样的悔界上界。对于OMD算法的active更新，同样可以得出类似的悔界分析结果，这里我们省略。当$R(w)=\frac{1}{2}\Vert w{\Vert }_2^2$时，OMD算法等价于OGD算法。如果使用其他的正则项函数 $R$,我们可以得出其他一些著名的算法。

Exponential Gradient (EG)

Exponential Gradient算法设 $R(w)=w\ln w$是负的熵函数，定义域是一个simplex满足$\mathcal{S}={\Delta }_d=\{w\in {\mathbb{R}}_{+}^d|{\sum }_i{w}_i=1\}$，此时OMD算法等价于exponential gradient(EG)算法。在这个特例中，投影为$L1norm$。每轮的更新法则为：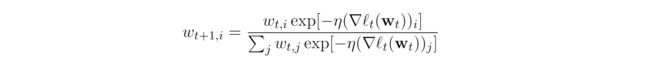

作为OMD的特殊情况，EG的悔值界为 $O(\sqrt{T})$。

Adaptive (Sub)-Gradient Methods

前面提到的算法中，在整个学习的过程中，正则项函数R是总数固定的且和数据无关。Adaptive Gradient算法可以看作是拥有自适应正则项的OMD算法，也就是说正则项函数 $R$ 会时刻变化。算法具体流程为在t时刻的正则项R等价于历史累计的梯度的统计结果，虽然严格意义上说仅仅利用了一阶的信息，但是它近似了二阶梯度的信息。

阅读论文

四、博弈论

博弈论与在线学习密切相关。一般来说，在线预测任务可以被描述为学习在学习者和环境之间进行重复游戏的问题。以在线分类为例，在每次迭代中，算法从有限数量的类中选择一个类，环境揭示真实的类标签。假设环境是稳定的(例如，独立同分布)。该算法的目标是达到最佳固定策略的效果。因此，经典的在线分类问题可以在最简单的假设、充分反馈和稳定的环境下用博弈论建模。更一般地说，博弈论中的各种设置可以与许多其他类型的在线学习问题相关。例如，反馈可能被部分观察到，或者环境不是独立同分布，或者可以由旨在最大化预测器损失的对手操作。

在本节中，我们将介绍一些关于博弈论的基本概念。

4.1 博弈与纳什均衡

K-Player Normal Form Games

考虑一个有 $K$ 个参与者 $(1<K<\infty )$的博弈，其中每个参与者 $k\in 1，\dots ，K$可以采取 $N_k$个可能的动作。玩家的行动可以用向量 $i=(i_1，\dots ，i_K),i_k\in 1，\dots ，N_k$表示参与者的动作。参与者 $k$ 遭受的损失用 ${\ell }^{(k)}$表示，因为损失不仅与参与人 $k$ 的行为有关，而且与所有其他参与人的行为有关。在游戏的每一次迭代中，每个参与者 $k$ 都试图采取行动，以尽量减少自己的损失。

使用混合策略，参与者 $k$ 根据概率分布$p^{(k)}=(p_1^{(k)},....,p_{N_k}^{(k)})$在动作集 $\{1,...,N_k\}$中采取行动。所有 $K$ 个参与者的行动可以表示为一个随机向量 $I=(I_1,...,I_K)$，其中 $I_k$ 是玩家 $k$ 的行动，是一个在 $\{1,...,N_k\}$集合上取值的随机变量。参与者 $k$ 的期望损失可以量化为：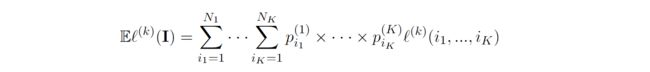

纳什均衡(Nash equilibrium)

这是博弈论中的一个重要概念。特别地，所有参与者 $p^{(1)}\times \cdot \cdot \cdot \times p^{(K)}$的集体策略被称为纳什均衡，如果 $K$ 个参与者)中的任意一个混合策略 $p^{(k)}$ 被任何新的混合策略 $q^{(k)}$ 所取代，而所有其他 $K-1$个参与人的混合策略没有改变，我们就有：
$$\mathbb{E}{\ell }^{(k)}(I)\le \mathbb{E}{\ell }^{(k)}(I^{\prime })$$
其中 $I^{\prime }$ 表示K个参与者使用新策略的行动。这个定义意味着在纳什均衡中，如果其他参与者不改变策略，没有参与者可以通过改变自己的策略来减少损失。在纳什均衡中，每个参与者都有自己的最优策略，并且没有改变策略的动机。人们可以证明每个有限博弈至少有一个纳什均衡，但一个博弈可能有多个纳什均衡，这取决于博弈的结构和损失函数。

4.2 重复的两方零和博弈

K-Player Normal Form Games的一个简单但重要的特殊类别是两方零和博弈游戏，其中只有一个玩家对阵一个对手，即 $K=2$ 。零和意味着对于任何行动，所有参与者的损失之和为零。这表明游戏是纯粹的竞争，一个参与者的损失导致另一个参与者的收获。在这种博弈中，第一个参与者通常被称为行参与者，第二个参与人被称为列参与者，其目标是使第一个参与人的损失最大化。

为了简化符号，我们认为行参与者有N个可能的操作，列参与者有M个可能的操作。我们用 $L\in [0,1{]}^{N\times M}$表示损失，其中 $L(i,j)$是行参与者采取行动 $i$ 而列参与者选择行动 $j $的损失，行参与者和列参与者的混合策略用 $p=(p，\dots ，pN)$ 和 $q=(q，\dots ，qN)$。对于 $p$ 和 $q$ 两种混合策略，行参与者的预期损失(相当于列参与者的预期收益)可以通过以下式子计算：
$$L(p,q)=\sum _{i=1}^N\sum _{j=1}^{M}p(i)q(j)L(i,j)$$
一对混合策略$(p,q)$是纳什均衡当且仅当:
$$L(p,q^{\prime })\le L(p,q)\le L(p^{\prime },q),\forall p^{\prime },\forall q^{\prime }$$
两方零和博弈的一个自然解决方案是遵循 minimax 解。

Minimax算法又名极小化极大算法，是一种找出失败的最大可能性中的最小值的算法。Minimax算法常用于棋类等由两方较量的游戏和程序，这类程序由两个游戏者轮流，每次执行一个步骤。我们众所周知的五子棋、象棋等都属于这类程序，所以说Minimax算法是基于搜索的博弈算法的基础。该算法是一种零总和算法，即一方要在可选的选项中选择将其优势最大化的选择，而另一方则选择令对手优势最小化的方法。

（1）Minimax是一种悲观算法，即假设对手每一步都会将我方引入从当前看理论上价值最小的格局方向，即对手具有完美决策能力。因此我方的策略应该是选择那些对方所能达到的让我方最差情况中最好的，也就是让对方在完美决策下所对我造成的损失最小。

（2）Minimax不找理论最优解，因为理论最优解往往依赖于对手是否足够愚蠢，Minimax中我方完全掌握主动，如果对方每一步决策都是完美的，则我方可以达到预计的最小损失格局，如果对方没有走出完美决策，则我方可能达到比预计的最悲观情况更好的结局。总之我方就是要在最坏情况中选择最好的。

我们现在可以把博弈论和在线学习联系起来，把它看作是学习重复玩二人零和游戏的问题。在在线学习环境中，行参与者也被称为学习者，列参与者被称为环境。行参与者和列参与者之间的重复博弈被视为学习者与环境之间进行 $T$ 轮交互的序列。在第 $t$ 轮，$t=1,...,T$：

• 学习者选择一个混合策略 $p_t$;
• 环境选择混合策略 $q_t$ (可能由知识 $p_t$ 选择);
• 学习者观察损失 $L(i,q_t)\forall i\in [N]$

一般来说，学习器的目标是使累积损失最小化，即${\sum }_{t=1}^{T}L(p_t,q_t)$。

引用

[1]Hoi S C H, Sahoo D, Lu J, et al. Online learning: A comprehensive survey[J]. Neurocomputing, 2021, 459: 249-289.点击阅读

[2] 数学上sup、inf含义，和max、min的区别

[3] 刘成昊. 在线学习算法研究与应用[D].浙江大学,2017.

[4] Minimax算法（极小化极大算法）及实例讲解