机器学习学习笔记之——模型评估与改进之交叉验证和网格搜索
交叉验证与网格搜索
前面讨论了监督学习和无监督学习的基本原理,并探索了多种机器学习算法,本章我们深入学习模型评估与参数选择。
我们将重点介绍监督方法,包括回归与分类,因为在无监督学习中,模型评估与选择通常是一个非常定性的过程。
到目前为止,为了评估我们的监督模型,我们使用 train_test_split 函数将数据集划分为训练集和测试集,在训练集上调用 fit 方法来构建模型,并且在测试集上用 score 方法来评估这个模型——对于分类问题而言,就是计算正确分类的样本所占的比例。下面是这个 过程的一个示例:
from sklearn.datasets import make_blobs
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# create a synthetic dataset
X, y = make_blobs(random_state=0)
# split data and labels into a training and a test set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# instantiate a model and fit it to the training set
logreg = LogisticRegression().fit(X_train, y_train)
# evaluate the model on the test set
print("Test set score: {:.2f}".format(logreg.score(X_test, y_test)))
# Test set score: 0.88
请记住,之所以将数据划分为训练集和测试集,是因为我们想要度量模型对前所未见的新数据的泛化性能。我们对模型在训练集上的拟合效果不感兴趣,而是想知道模型对于训练过程中没有见过的数据的预测能力。
本章我们将从两个方面进行模型评估。我们首先介绍交叉验证,然后讨论评估分类和回归性能的方法,其中前者是一种更可靠的评估泛化性能的方法,后者是在默认度量(score 方法给出的精度和 R2 )之外的方法。
我们还将讨论网格搜索,这是一种调节监督模型参数以获得最佳泛化性能的有效方法。
1、交叉验证
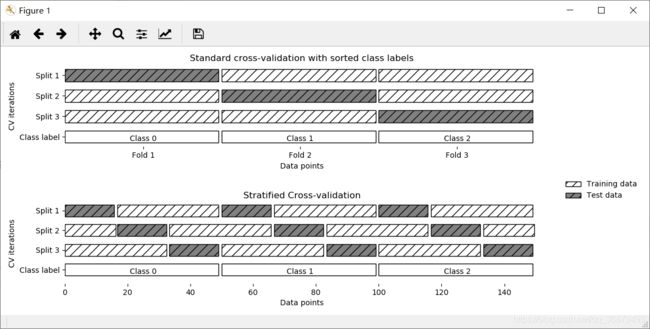
交叉验证(cross-validation)是一种评估泛化性能的统计学方法,它比单次划分训练集和测试集的方法更加稳定、全面。在交叉验证中,数据被多次划分,并且需要训练多个模型。 最常用的交叉验证是 k 折交叉验证(k-fold cross-validation),其中 k 是由用户指定的数字, 通常取 5 或 10。在执行 5 折交叉验证时,首先将数据划分为(大致)相等的 5 部分,每一部分叫作折(fold)。接下来训练一系列模型。使用第 1 折作为测试集、其他折(2~5)作为训练集来训练第一个模型。利用 2~5 折中的数据来构建模型,然后在 1 折上评估精度。 之后构建另一个模型,这次使用 2 折作为测试集,1、3、4、5 折中的数据作为训练集。利用 3、4、5 折作为测试集继续重复这一过程。对于将数据划分为训练集和测试集的这 5 次划分,每一次都要计算精度。最后我们得到了 5 个精度值。整个过程如下图所示。
mglearn.plots.plot_cross_validation()

通常来说,数据的前五分之一是第 1 折,第二个五分之一是第 2 折,以此类推。
1.1、scikit-learn 中的交叉验证
scikit-learn 是利用 model_selection 模块中的 cross_val_score 函数来实现交叉验证的。 cross_val_score 函数的参数是我们想要评估的模型、训练数据与真实标签。我们在 iris 数据集上对 LogisticRegression 进行评估:
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
iris = load_iris()
logreg = LogisticRegression(max_iter=1000)
scores = cross_val_score(logreg, iris.data, iris.target)
print("Cross-validation scores: {}".format(scores))
# Cross-validation scores: [0.96666667 1. 0.93333333 0.96666667 1. ]
默认情况下,cross_val_score 执行 5 折交叉验证,返回 5 个精度值。可以通过修改 cv 参数来改变折数:
scores = cross_val_score(logreg, iris.data, iris.target, cv=3)
print("Cross-validation scores: {}".format(scores))
# Cross-validation scores: [0.98 0.96 0.98]
总结交叉验证精度的一种常用方法是计算平均值:
print("Average cross-validation score: {:.2f}".format(scores.mean()))
# Average cross-validation score: 0.97
我们可以从交叉验证平均值中得出结论,我们预计模型的平均精度约为 96%。观察 5 折交叉验证得到的所有 5 个精度值,我们还可以发现,折与折之间的精度有较大的变化,范围为从 100% 精度到 90% 精度。这可能意味着模型强烈依赖于将某个折用于训练,但也可能只是因为数据集的数据量太小。
1.2、交叉验证的优点
使用交叉验证而不是将数据单次划分为训练集和测试集,这种做法具有下列优点。
- 首先,
train_test_split对数据进行随机划分。想象一下,在随机划分数据时我们很 “幸运”,所有难以分类的样例都在训练集中。在这种情况下,测试集将仅包含 “容易分类的” 样例, 并且测试集精度会高得不切实际。相反,如果我们 “不够幸运”,则可能随机地将所有难以分类的样例都放在测试集中,因此得到一个不切实际的低分数。但如果使用交叉验证, 每个样例都会刚好在测试集中出现一次:每个样例位于一个折中,而每个折都在测试集中出现一次。因此,模型需要对数据集中所有样本的泛化能力都很好,才能让所有的交叉验证得分(及其平均值)都很高。 - 对数据进行多次划分,还可以提供我们的模型对训练集选择的敏感性信息。对于
iris数据 集,我们观察到精度在 90% 到 100% 之间。这是一个不小的范围,它告诉我们将模型应用于新数据时在最坏情况和最好情况下的可能表现。 - 与数据的单次划分相比,交叉验证的另一个优点是我们对数据的使用更加高效。在使用
train_test_split时,我们通常将 75% 的数据用于训练,25% 的数据用于评估。在使用 5 折交叉验证时,在每次迭代中我们可以使用 4/5(80%)的数据来拟合模型。在使用 10 折交叉验证时,我们可以使用 9/10(90%)的数据来拟合模型。更多的数据通常可以得到更为精确的模型。
缺点:
- 交叉验证的主要缺点是增加了计算成本。现在我们要训练 k 个模型而不是单个模型,所以 交叉验证的速度要比数据的单次划分大约慢 k 倍。
重要的是要记住,交叉验证不是一种构建可应用于新数据的模型的方法。交叉验证不会返回一个模型。在调用
cross_val_score时,内部会构建多个模型,但交叉验证的目的只是评估给定算法在特定数据集上训练后的泛化性能好坏。
1.3、分层 k 折交叉验证和其他策略
将数据集划分为 k 折时,从数据的前 k 分之一开始划分(正如上一节所述),这可能并不总 是一个好主意。例如,我们来看一下 iris 数据集:
from sklearn.datasets import load_iris
iris = load_iris()
print("Iris labels:\n{}".format(iris.target))
'''
Iris labels:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
'''
如你所见,数据的前三分之一是类别 0,中间三分之一是类别 1,最后三分之一是类别 2。 想象一下在这个数据集上进行 3 折交叉验证。第 1 折将只包含类别 0,所以在数据的第一次划分中,测试集将只包含类别 0,而训练集只包含类别 1 和 2。由于在 3 次划分中训练集和测试集中的类别都不相同,因此这个数据集上的 3 折交叉验证精度为 0。这没什么帮助,因为我们在 iris 上可以得到比 0% 好得多的精度。
由于简单的 k 折策略在这里失效了,所以 scikit-learn 在分类问题中不使用这种策略,而 是使用分层 k 折交叉验证(stratified k-fold cross-validation)。在分层交叉验证中,我们划分数据,使每个折中类别之间的比例与整个数据集中的比例相同,如下图所示。
mglearn.plots.plot_stratified_cross_validation()
举个例子,如果 90% 的样本属于类别 A 而 10% 的样本属于类别 B,那么分层交叉验证可以确保,在每个折中 90% 的样本属于类别 A 而 10% 的样本属于类别 B。
使用分层 k 折交叉验证而不是 k 折交叉验证来评估一个分类器,这通常是一个好主意,因 为它可以对泛化性能做出更可靠的估计。在只有 10% 的样本属于类别 B 的情况下,如果使用标准 k 折交叉验证,很可能某个折中只包含类别 A 的样本。利用这个折作为测试集的话,无法给出分类器整体性能的信息。
对于回归问题,scikit-learn 默认使用标准 k 折交叉验证。也可以尝试让每个折表示回归目标的不同取值,但这并不是一种常用的策略,也会让大多数用户感到意外。
1.3.1、对交叉验证的更多控制
我们之前看到,可以利用 cv 参数来调节 cross_val_score 所使用的折数。但 scikit-learn 允许提供一个交叉验证分离器(cross-validation splitter)作为 cv 参数,来对数据划分过程进行更精细的控制。对于大多数使用场景而言,回归问题默认的 k 折交叉验证与分类问题的分层 k 折交叉验证的表现都很好,但有些情况下你可能希望使用不同的策略。比如说, 我们想要在一个分类数据集上使用标准 k 折交叉验证来重现别人的结果。为了实现这一 点,我们首先必须从 model_selection 模块中导入 KFold 分离器类,并用我们想要使用的折数来将其实例化:
from sklearn.model_selection import KFold
kfold = KFold(n_splits=5)
然后我们可以将 kfold 分离器对象作为 cv 参数传入 cross_val_score:
print("Cross-validation scores:\n{}".format(
cross_val_score(logreg, iris.data, iris.target, cv=kfold)))
'''
Cross-validation scores:
[1. 1. 0.86666667 0.93333333 0.83333333]
'''
通过这种方法,我们可以验证,在 iris 数据集上使用 3 折交叉验证(不分层)确实是一个非常糟糕的主意:
kfold = KFold(n_splits=3)
print("Cross-validation scores:\n{}".format(
cross_val_score(logreg, iris.data, iris.target, cv=kfold)))
'''
Cross-validation scores:
[0. 0. 0.]
'''
请记住,在 iris 数据集中每个折对应一个类别,因此学不到任何内容。解决这个问题的另一种方法是将数据打乱来代替分层,以打乱样本按标签的排序。可以通过将 KFold 的 shuffle 参数设为 True 来实现这一点。如果我们将数据打乱,那么还需要固定 random_ state 以获得可重复的打乱结果。否则,每次运行 cross_val_score 将会得到不同的结果, 因为每次使用的是不同的划分(这可能并不是一个问题,但可能会出人意料)。在划分数据之前将其打乱可以得到更好的结果:
kfold = KFold(n_splits=3, shuffle=True, random_state=0)
print("Cross-validation scores:\n{}".format(
cross_val_score(logreg, iris.data, iris.target, cv=kfold)))
'''
Cross-validation scores:
[0.98 0.96 0.96]
'''
1.3.2、留一法交叉验证
另一种常用的交叉验证方法是留一法(leave-one-out)。你可以将留一法交叉验证看作是每折只包含单个样本的 k 折交叉验证。对于每次划分,你选择单个数据点作为测试集。这种方法可能非常耗时,特别是对于大型数据集来说,但在小型数据集上有时可以给出更好的估计结果:
from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()
scores = cross_val_score(logreg, iris.data, iris.target, cv=loo)
print("Number of cv iterations: ", len(scores))
# Number of cv iterations: 150
print("Mean accuracy: {:.2f}".format(scores.mean()))
# Mean accuracy: 0.97
1.3.3、打乱划分交叉验证
另一种非常灵活的交叉验证策略是打乱划分交叉验证(shuffle-split cross-validation)。在打乱划分交叉验证中,每次划分为训练集取样 train_size 个点,为测试集取样 test_size 个 (不相交的)点。将这一划分方法重复 n_iter 次。下图显示的是对包含 10 个点的数据集运行 4 次迭代划分,每次的训练集包含 5 个点,测试集包含 2 个点(你可以将 train_size 和 test_size 设为整数来表示这两个集合的绝对大小,也可以设为浮点数来表示占整个数据集的比例):
mglearn.plots.plot_shuffle_split()
下面的代码将数据集划分为 50% 的训练集和 50% 的测试集,共运行 10 次迭代 :
from sklearn.model_selection import ShuffleSplit
shuffle_split = ShuffleSplit(test_size=.5, train_size=.5, n_splits=10)
scores = cross_val_score(logreg, iris.data, iris.target, cv=shuffle_split)
print("Cross-validation scores:\n{}".format(scores))
'''
Cross-validation scores:
[0.97333333 0.96 0.90666667 0.92 0.94666667 0.97333333
0.97333333 0.94666667 0.97333333 0.93333333]
'''
打乱划分交叉验证可以在训练集和测试集大小之外独立控制迭代次数,这有时是很有帮助的。它还允许在每次迭代中仅使用部分数据,这可以通过设置 train_size 与 test_size 之和不等于 1 来实现。用这种方法对数据进行二次采样可能对大型数据上的试验很有用。
ShuffleSplit 还有一种分层的形式,其名称为 StratifiedShuffleSplit,它可以为分类任务提供更可靠的结果。
1.3.4、分组交叉验证
另一种非常常见的交叉验证适用于数据中的分组高度相关时。比如你想构建一个从人脸图片中识别情感的系统,并且收集了 100 个人的照片的数据集,其中每个人都进行了多次拍摄,分别展示了不同的情感。我们的目标是构建一个分类器,能够正确识别未包含在数据集中的人的情感。你可以使用默认的分层交叉验证来度量分类器的性能。但是这样的话, 同一个人的照片可能会同时出现在训练集和测试集中。对于分类器而言,检测训练集中出现过的人脸情感比全新的人脸要容易得多。因此,为了准确评估模型对新的人脸的泛化能力,我们必须确保训练集和测试集中包含不同人的图像。
为了实现这一点,我们可以使用 GroupKFold,它以 groups 数组作为参数,可以用来说明照片中对应的是哪个人。这里的 groups 数组表示数据中的分组,在创建训练集和测试集的时候不应该将其分开,也不应该与类别标签弄混。
数据分组的这种例子常见于医疗应用,你可能拥有来自同一名病人的多个样本,但想要将其泛化到新的病人。同样,在语音识别领域,你的数据集中可能包含同一名发言人的多条 记录,但你希望能够识别新的发言人的讲话。
下面这个示例用到了一个由 groups 数组指定分组的模拟数据集。这个数据集包含 12 个数据点,且对于每个数据点,groups 指定了该点所属的分组(想想病人的例子)。一共分成 4 个组,前 3 个样本属于第一组,接下来的 4 个样本属于第二组,以此类推:
from sklearn.model_selection import GroupKFold
# 创建模拟数据集
X, y = make_blobs(n_samples=12, random_state=0)
# 假设前 3 个样本属于同一组,接下来的 4 个属于同一组,以此类推
# then the next four, etc.
groups = [0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3, 3]
scores = cross_val_score(logreg, X, y, groups=groups, cv=GroupKFold(n_splits=3))
print("Cross-validation scores:\n{}".format(scores))
'''
Cross-validation scores:
[0.75 0.6 0.66666667]
'''
样本不需要按分组进行排序,我们这么做只是为了便于说明。基于这些标签计算得到的划分如下图所示。
如你所见,对于每次划分,每个分组都是整体出现在训练集或测试集中:
mglearn.plots.plot_group_kfold()
scikit-learn 中还有很多交叉验证的划分策略,适用于更多的使用场景 [ 你可以在 scikitlearn 的用户指南页面查看这些内容(http://scikit-learn.org/stable/modules/cross_validation. html)]。但标准的 KFold、StratifiedKFold 和 GroupKFold 是目前最常用的几种。
2、网格搜索
现在我们知道了如何评估一个模型的泛化能力,下面继续学习通过调参来提升模型的泛化性能。在前面的各种算法中讨论过 scikit-learn 中许多算法的参数设置,在尝试调参之前, 重要的是要理解参数的含义。找到一个模型的重要参数(提供最佳泛化性能的参数)的取值是一项棘手的任务,但对于几乎所有模型和数据集来说都是必要的。由于这项任务如此常见,所以 scikit-learn 中有一些标准方法可以帮你完成。最常用的方法就是网格搜索(grid search),它主要是指尝试我们关心的参数的所有可能组合。
考虑一个具有 RBF(径向基函数)核的核 SVM 的例子,它在 SVC 类中实现。正如前面介绍时中所述,它有 2 个重要参数:核宽度 gamma 和正则化参数 C。假设我们希望尝试 C 的取值为 0.001、0.01、0.1、1、10 和 100,gamma 也取这 6 个值。由于我想要尝试的 C 和 gamma 都有 6 个不同的取值,所以总共有 36 种参数组合。所有可能的组合组成了 SVM 的参数设置表(网格),如下所示。
| C=0.001 | C=0.01 | … | C=10 | |
|---|---|---|---|---|
| gamma=0.001 | SVC(C=0.001, gamma=0.001) | SVC(C=0.01, gamma=0.001) | … | SVC(C=10, gamma=0.001) |
| gamma=0.01 | SVC(C=0.001, gamma=0.01) | SVC(C=0.01, gamma=0.01) | … | SVC(C=10, gamma=0.01) |
| … | … | … | … | … |
| gamma=10 | SVC(C=0.001, gamma=10) | SVC(C=0.01, gamma=10) | SVC(C=10, gamma=10) |
2.1、简单的网格搜索
我们可以实现一个简单的网格搜索,在 2 个参数上使用 for 循环,对每种参数组合分别训练并评估一个分类器:
from sklearn.svm import SVC
X_train, X_test, y_train, y_test = train_test_split(
iris.data, iris.target, random_state=0)
print("Size of training set: {} size of test set: {}".format(
X_train.shape[0], X_test.shape[0]))
# Size of training set: 112 size of test set: 38
best_score = 0
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# 对每种参数组合都训练一个SVC
svm = SVC(gamma=gamma, C=C)
svm.fit(X_train, y_train)
# 在测试集上评估SVC
score = svm.score(X_test, y_test)
# 如果我们得到了更高的分数,则保存该分数和对应的参数
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
print("Best score: {:.2f}".format(best_score))
# Best score: 0.97
print("Best parameters: {}".format(best_parameters))
# Best parameters: {'C': 100, 'gamma': 0.001}
2.2、参数过拟合的风险与验证集
看到这个结果,我们可能忍不住要报告,我们找到了一个在数据集上精度达到 97% 的模型。然而,这种说法可能过于乐观了(或者就是错的),其原因如下:我们尝试了许多不同的参数,并选择了在测试集上精度最高的那个,但这个精度不一定能推广到新数据上。 由于我们使用测试数据进行调参,所以不能再用它来评估模型的好坏。我们最开始需要将数据划分为训练集和测试集也是因为这个原因。我们需要一个独立的数据集来进行评估, 一个在创建模型时没有用到的数据集。
为了解决这个问题,一种方法是再次划分数据,这样我们得到 3 个数据集:用于构建模型的训练集,用于选择模型参数的验证集(开发集),用于评估所选参数性能的测试集。下图给出了这 3 个集合的图示:
mglearn.plots.plot_threefold_split()
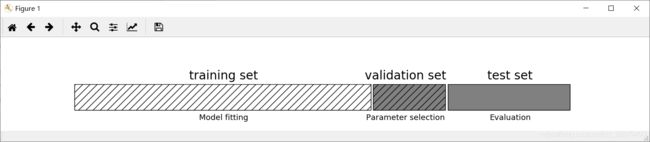
利用验证集选定最佳参数之后,我们可以利用找到的参数设置重新构建一个模型,但是要同时在训练数据和验证数据上进行训练。这样我们可以利用尽可能多的数据来构建模型。 其实现如下所示:
from sklearn.svm import SVC
# 将数据划分为训练+验证集与测试集
X_trainval, X_test, y_trainval, y_test = train_test_split(
iris.data, iris.target, random_state=0)
# 将训练+验证集划分为训练集与验证集
X_train, X_valid, y_train, y_valid = train_test_split(
X_trainval, y_trainval, random_state=1)
print("Size of training set: {} size of validation set: {} size of test set:"
" {}\n".format(X_train.shape[0], X_valid.shape[0], X_test.shape[0]))
# Size of training set: 84 size of validation set: 28 size of test set: 38
best_score = 0
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# 对每种参数组合都训练一个SVC
svm = SVC(gamma=gamma, C=C)
svm.fit(X_train, y_train)
# 在验证集上评估SVC
score = svm.score(X_valid, y_valid)
# 如果我们得到了更高的分数,则保存该分数和对应的参数
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
# 在训练+验证集上重建一个模型,并在测试集上进行评估
svm = SVC(**best_parameters)
svm.fit(X_trainval, y_trainval)
test_score = svm.score(X_test, y_test)
print("Best score on validation set: {:.2f}".format(best_score))
# Best score on validation set: 0.96
print("Best parameters: ", best_parameters)
# Best parameters: {'C': 10, 'gamma': 0.001}
print("Test set score with best parameters: {:.2f}".format(test_score))
# Test set score with best parameters: 0.92
验证集上的最高分数是 96%,这比之前略低,可能是因为我们使用了更少的数据来训练模 型(现在 X_train 更小,因为我们对数据集做了两次划分)。但测试集上的分数(这个分数实际反映了模型的泛化能力)更低,为 92%。因此,我们只能声称对 92% 的新数据正确分类,而不是我们之前认为的 97% !
训练集、验证集和测试集之间的区别对于在实践中应用机器学习方法至关重要。任何根据测试集精度所做的选择都会将测试集的信息 “泄漏”(leak)到模型中。因此,保留一个单独的测试集是很重要的,它仅用于最终评估。好的做法是利用训练集和验证集的组合完成所有的探索性分析与模型选择,并保留测试集用于最终评估——即使对于探索性可视化也是如此。严格来说,在测试集上对不止一个模型进行评估并选择更好的那个,将会导致对模型精度过于乐观的估计。
2.3、带交叉验证的网格搜索
虽然将数据划分为训练集、验证集和测试集的方法(如上所述)是可行的,也相对常用,但这种方法对数据的划分方法相当敏感。从上面代码片段的输出中可以看出,网格搜索选择 'C': 10, 'gamma': 0.001 作为最佳参数,而前面的代码输出选择 'C': 100, 'gamma': 0.001 作为最佳参数。为了得到对泛化性能的更好估计,我们可以使用交叉验证来评估每种参数组合的性能,而不是仅将数据单次划分为训练集与验证集。这种方法用代码表示如下:
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# 对于每种参数组合都训练一个SVC
svm = SVC(gamma=gamma, C=C)
# 执行交叉验证
scores = cross_val_score(svm, X_trainval, y_trainval, cv=5)
# 计算交叉验证平均精度
score = np.mean(scores)
# 如果我们得到了更高的分数,则保存该分数和对应的参数
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
# 在训练+验证集上重新构建一个模型
svm = SVC(**best_parameters)
svm.fit(X_trainval, y_trainval)
要想使用 5 折交叉验证对 C 和 gamma 特定取值的 SVM 的精度进行评估,需要训练 36×5 = 180 个模型。你可以想象,使用交叉验证的主要缺点就是训练所有这些模型所需花费的时间。
下面的可视化说明了上述代码如何选择最佳参数设置:
mglearn.plots.plot_cross_val_selection()
对于每种参数设置(图中仅显示了一部分),需要计算 5 个精度值,交叉验证的每次划分都要计算一个精度值。然后,对每种参数设置计算平均验证精度。最后,选择平均验证精度最高的参数,用圆圈标记。
如前所述,交叉验证是在特定数据集上对给定算法进行评估的一种方法。但它通常与网格搜索等参数搜索方法结合使用。因此,许多人使用交叉验证 (
cross-validation)这一术语来通俗地指代带交叉验证的网格搜索。
划分数据、运行网格搜索并评估最终参数,这整个过程如下图所示。
mglearn.plots.plot_grid_search_overview()
由于带交叉验证的网格搜索是一种常用的调参方法, 因此 scikit-learn 提供了 GridSearchCV 类,它以估计器(estimator)的形式实现了这种方法。要使用 GridSearchCV 类,你首先需要用一个字典指定要搜索的参数。然后 GridSearchCV 会执行所有必要的模型拟合。字典的键是我们要调节的参数名称(在构建模型时给出,在这个例子中是 C 和 gamma),字典的值是我们想要尝试的参数设置。如果 C 和 gamma 想要尝试的取值为 0.001、 0.01、0.1、1、10 和 100,可以将其转化为下面这个字典:
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
print("Parameter grid:\n{}".format(param_grid))
'''
Parameter grid:
{'C': [0.001, 0.01, 0.1, 1, 10, 100], 'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
'''
现在我们可以使用模型(SVC)、要搜索的参数网格(param_grid)与要使用的交叉验证策略(比如 5 折分层交叉验证)将 GridSearchCV 类实例化:
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
grid_search = GridSearchCV(SVC(), param_grid, cv=5, return_train_score=True)
GridSearchCV 将使用交叉验证来代替之前用过的划分训练集和验证集方法。但是,我们仍需要将数据划分为训练集和测试集,以避免参数过拟合:
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=0)
我们创建的 grid_search 对象的行为就像是一个分类器,我们可以对它调用标准的 fit、 predict 和 score 方法。但我们在调用 fit 时,它会对 param_grid 指定的每种参数组合都运行交叉验证:
grid_search.fit(X_train, y_train)
拟合 GridSearchCV 对象不仅会搜索最佳参数,还会利用得到最佳交叉验证性能的参数在整个训练数据集上自动拟合一个新模型。GridSearchCV 类提供了一个非常方便的接口,可以用 predict 和 score 方 法来访问重新训练过的模型。为了评估找到的最佳参数的泛化能力,我们可以在测试集上调用 score:
print("Test set score: {:.2f}".format(grid_search.score(X_test, y_test)))
# Test set score: 0.97
利用交叉验证选择参数,我们实际上找到了一个在测试集上精度为 97% 的模型。重要的是,我们没有使用测试集来选择参数。我们找到的参数保存在 best_params_ 属性中,而交叉验证最佳精度(对于这种参数设置,不同划分的平均精度)保存在 best_score_ 中:
print("Best parameters: {}".format(grid_search.best_params_))
# Best parameters: {'C': 10, 'gamma': 0.1}
print("Best cross-validation score: {:.2f}".format(grid_search.best_score_))
# Best cross-validation score: 0.97
同样,注意不要将
best_score_与模型在测试集上调用score方法计算得到的泛化性能弄混。使用score方法(或者对predict方法的输出进行评估) 采用的是在整个训练集上训练的模型。而best_score_属性保存的是交叉验证的平均精度,是在训练集上进行交叉验证得到的。
能够访问实际找到的模型,这有时是很有帮助的,比如查看系数或特征重要性。你可以用 best_estimator_ 属性来访问最佳参数对应的模型,它是在整个训练集上训练得到的:
print("Best estimator:\n{}".format(grid_search.best_estimator_))
'''
Best estimator:
SVC(C=10, gamma=0.1)
'''
由于 grid_search 本身具有 predict 和 score 方法,所以不需要使用 best_estimator_ 来进 行预测或评估模型。
2.3.1、分析交叉验证的结果
将交叉验证的结果可视化通常有助于理解模型泛化能力对所搜索参数的依赖关系。由于运行网格搜索的计算成本相当高,所以通常最好从相对比较稀疏且较小的网格开始搜索。然后我们可以检查交叉验证网格搜索的结果,可能也会扩展搜索范围。网格搜索的结果可以在 cv_results_ 属性中找到,它是一个字典,其中保存了搜索的所有内容。你可以在下面的输出中看到,它里面包含许多细节,最好将其转换成 pandas 数据框后再查看:
import pandas as pd
# 转换为DataFrame(数据框)
results = pd.DataFrame(grid_search.cv_results_)
# 显示前5行
print(results.head())
'''
mean_fit_time ... std_train_score
0 0.000581 ... 0.005581
1 0.000601 ... 0.005581
2 0.000799 ... 0.005581
3 0.000601 ... 0.005581
4 0.000597 ... 0.005581
[5 rows x 22 columns]
'''
results 中每一行对应一种特定的参数设置。对于每种参数设置,交叉验证所有划分的结果都被记录下来,所有划分的平均值和标准差也被记录下来。由于我们搜索的是一个二维参数网格(C 和 gamma),所以最适合用热图可视化。我们首先提取平均验证分数,然后改变分数数组的形状,使其坐标轴分别对应于 C 和 gamma:
scores = np.array(results.mean_test_score).reshape(6, 6)
# 对交叉验证平均分数作图
mglearn.tools.heatmap(scores, xlabel='gamma', xticklabels=param_grid['gamma'],
ylabel='C', yticklabels=param_grid['C'], cmap="viridis")
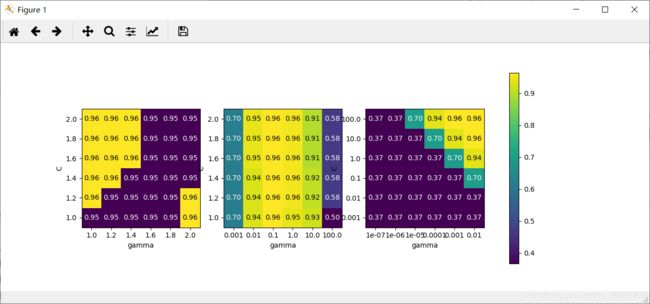
热图中的每个点对应于运行一次交叉验证以及一种特定的参数设置。颜色表示交叉验证的精度:浅色表示高精度,深色表示低精度。你可以看到,SVC 对参数设置非常敏感。对于许多种参数设置,精度都在 40% 左右,这是非常糟糕的;对于其他参数设置,精度约为 96%。我们可以从这张图中看出以下几点。首先,我们调节的参数对于获得良好的性能非常重要。这两个参数(C 和 gamma)都很重要,因为调节它们可以将精度从 40% 提高到 96%。此外,在我们选择的参数范围中也可以看到输出发生了显著的变化。同样重要的是要注意,参数的范围要足够大:每个参数的最佳取值不能位于图像的边界上。
下面我们来看几张图,其结果不那么理想,因为选择的搜索范围不合适。
fig, axes = plt.subplots(1, 3, figsize=(13, 5))
param_grid_linear = {'C': np.linspace(1, 2, 6),
'gamma': np.linspace(1, 2, 6)}
param_grid_one_log = {'C': np.linspace(1, 2, 6),
'gamma': np.logspace(-3, 2, 6)}
param_grid_range = {'C': np.logspace(-3, 2, 6),
'gamma': np.logspace(-7, -2, 6)}
for param_grid, ax in zip([param_grid_linear, param_grid_one_log,
param_grid_range], axes):
grid_search = GridSearchCV(SVC(), param_grid, cv=5)
grid_search.fit(X_train, y_train)
scores = grid_search.cv_results_['mean_test_score'].reshape(6, 6)
# plot the mean cross-validation scores
scores_image = mglearn.tools.heatmap(
scores, xlabel='gamma', ylabel='C', xticklabels=param_grid['gamma'],
yticklabels=param_grid['C'], cmap="viridis", ax=ax)
plt.colorbar(scores_image, ax=axes.tolist())
第一张图没有显示任何变化,整个参数网格的颜色相同。在这种情况下,这是由参数 C 和 gamma 不正确的缩放以及不正确的范围造成的。但如果对于不同的参数设置都看不到精度的变化,也可能是因为这个参数根本不重要。通常最好在开始时尝试非常极端的值,以观察改变参数是否会导致精度发生变化。
第二张图显示的是垂直条形模式。这表示只有 gamma 的设置对精度有影响。这可能意味着 gamma 参数的搜索范围是我们所关心的,而 C 参数并不是——也可能意味着 C 参数并不重要。
第三张图中 C 和 gamma 对应的精度都有变化。但可以看到,在图像的整个左下角都没有发 生什么有趣的事情。我们在后面的网格搜索中可以不考虑非常小的值。最佳参数设置出现在右上角。由于最佳参数位于图像的边界,所以我们可以认为,在这个边界之外可能还有更好的取值,我们可能希望改变搜索范围以包含这一区域内的更多参数。
基于交叉验证分数来调节参数网格是非常好的,也是探索不同参数的重要性的好方法。但是,你不应该在最终测试集上测试不同的参数范围——前面说过,只有确切知道了想要使用的模型,才能对测试集进行评估。
2.3.2、在非网格的空间中搜索
在某些情况下,尝试所有参数的所有可能组合(正如 GridSearchCV 所做的那样)并不是一个好主意。例如,SVC 有一个 kernel 参数,根据所选择的 kernel(内核),其他参数也是与之相关的。如果 kernel='linear',那么模型是线性的,只会用到 C 参数。如果 kernel='rbf',则需要使用 C 和 gamma 两个参数(但用不到类似 degree 的其他参数)。在这种情况下,搜索 C、gamma 和 kernel 所有可能的组合没有意义:如果 kernel='linear', 那么 gamma 是用不到的,尝试 gamma 的不同取值将会浪费时间。为了处理这种 “条件”(conditional)参数,GridSearchCV 的 param_grid 可以是字典组成的列表(a list of dictionaries)。列表中的每个字典可扩展为一个独立的网格。包含内核与参数的网格搜索可能如下所示。
param_grid = [{'kernel': ['rbf'],
'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]},
{'kernel': ['linear'],
'C': [0.001, 0.01, 0.1, 1, 10, 100]}]
print("List of grids:\n{}".format(param_grid))
'''
List of grids:
[{'kernel': ['rbf'], 'C': [0.001, 0.01, 0.1, 1, 10, 100], 'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}, {'kernel': ['linear'], 'C': [0.001, 0.01, 0.1, 1, 10, 100]}]
'''
在第一个网格中,kernel 参数始终等于 ‘rbf’(注意 kernel 是一个长度为 1 的列表),而 C 和 gamma 都是变化的。在第二个网格中,kernel 参数始终等于 ‘linear’,只有 C 是变化 的。下面我们来应用这个更加复杂的参数搜索:
grid_search = GridSearchCV(SVC(), param_grid, cv=5,
return_train_score=True)
grid_search.fit(X_train, y_train)
print("Best parameters: {}".format(grid_search.best_params_))
# Best parameters: {'C': 10, 'gamma': 0.1, 'kernel': 'rbf'}
print("Best cross-validation score: {:.2f}".format(grid_search.best_score_))
# Best cross-validation score: 0.97
我们再次查看 cv_results_。正如所料,如果 kernel 等于 ‘linear’,那么只有 C 是变化的:
results = pd.DataFrame(grid_search.cv_results_)
# we display the transposed table so that it better fits on the page:
print(results.T)
2.3.3、使用不同的交叉验证策略进行网格搜索
与 cross_val_score 类似,GridSearchCV 对分类问题默认使用分层 k 折交叉验证,对回归问题默认使用 k 折交叉验证。但是,你可以传入任何交叉验证分离器作为 GridSearchCV 的 cv 参数。特别地,如果只想将数据单次划分为训练集和验证集,你可以使用 ShuffleSplit 或 StratifiedShuffleSplit,并 设置 n_iter=1。这对于非常大的数据集或非常慢的模型可能会有帮助。
-
嵌套交叉验证
在前面的例子中,我们先介绍了将数据单次划分为训练集、验证集与测试集,然后介绍了先将数据划分为训练集和测试集,再在训练集上进行交叉验证。但前面在使用
GridSearchCV时,我们仍然将数据单次划分为训练集和测试集,这可能会导致结果不稳定,也让我们过于依赖数据的此次划分。我们可以再深入一点,不是只将原始数据一次划分为训练集和测试集,而是使用交叉验证进行多次划分,这就是所谓的嵌套交叉验证 (nested cross-validation)。在嵌套交叉验证中,有一个外层循环,遍历将数据划分为训练 集和测试集的所有划分。对于每种划分都运行一次网格搜索(对于外层循环的每种划分可能会得到不同的最佳参数)。然后,对于每种外层划分,利用最佳参数设置计算得到测试集分数。这一过程的结果是由分数组成的列表——不是一个模型,也不是一种参数设置。这些分数告诉我们在网格找到的最佳参数下模型的泛化能力好坏。由于嵌套交叉验证不提供可用于新数据的模型,所以在寻找可用于未来数据的预测模型时很少用到它。但是,它对于评估给定模型在特定数据集上的效果很有用。
在
scikit-learn中实现嵌套交叉验证很简单。我们调用cross_val_score,并用GridSearchCV的一个实例作为模型:param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100], 'gamma': [0.001, 0.01, 0.1, 1, 10, 100]} scores = cross_val_score(GridSearchCV(SVC(), param_grid, cv=5), iris.data, iris.target, cv=5) print("Cross-validation scores: ", scores) # Cross-validation scores: [0.96666667 1. 0.96666667 0.96666667 1. ] print("Mean cross-validation score: ", scores.mean()) # Mean cross-validation score: 0.9800000000000001嵌套交叉验证的结果可以总结为 “
SVC在iris数据集上的交叉验证平均精度为 98%”—— 不多也不少。这里我们在内层循环和外层循环中都使用了分层 5 折交叉验证。由于
param_grid包含 36 种参数组合,所以需要构建 36×5×5 = 900 个模型,导致嵌套交叉验证过程的代价很高。 这里我们在内层循环和外层循环中使用相同的交叉验证分离器,但这不是必需的,你可以在内层循环和外层循环中使用交叉验证策略的任意组合。理解上面单行代码的内容可能有点困难,将其展开为for循环可能会有所帮助,正如我们在下面这个简化的实现中所做的那样:def nested_cv(X, y, inner_cv, outer_cv, Classifier, parameter_grid): outer_scores = [] # 对于外层交叉验证的每次数据划分,split 方法返回索引值 for training_samples, test_samples in outer_cv.split(X, y): # 利用内层交叉验证找到最佳参数 best_parms = {} best_score = -np.inf # 遍历参数 for parameters in parameter_grid: # 在内层划分中累加分数 cv_scores = [] # 遍历内层交叉验证 for inner_train, inner_test in inner_cv.split( X[training_samples], y[training_samples]): # 对于给定的参数和训练数据来构建分类器 clf = Classifier(**parameters) clf.fit(X[inner_train], y[inner_train]) # 在内层测试集上进行评估 score = clf.score(X[inner_test], y[inner_test]) cv_scores.append(score) # 计算内层交叉验证的平均分数 mean_score = np.mean(cv_scores) if mean_score > best_score: # 如果比前面的模型都要好,则保存其参数 best_score = mean_score best_params = parameters # 利用外层训练集和最佳参数来构建模型 clf = Classifier(**best_params) clf.fit(X[training_samples], y[training_samples]) # 评估模型 outer_scores.append(clf.score(X[test_samples], y[test_samples])) return np.array(outer_scores)下面我们在
iris数据集上运行这个函数:from sklearn.model_selection import ParameterGrid, StratifiedKFold scores = nested_cv(iris.data, iris.target, StratifiedKFold(5), StratifiedKFold(5), SVC, ParameterGrid(param_grid)) print("Cross-validation scores: {}".format(scores)) # Cross-validation scores: [0.96666667 1. 0.96666667 0.96666667 1. ] -
交叉验证与网格搜索并行
虽然在许多参数上运行网格搜索和在大型数据集上运行网格搜索的计算量可能很大,但令人尴尬的是,这些计算都是并行的(
parallel)。这也就是说,在一种交叉验证划分下使用特定参数设置来构建一个模型,与利用其他参数的模型是完全独立的。这使得网格搜索与交叉验证成为多个 CPU 内核或集群上并行化的理想选择。你可以将n_jobs参数设置为你想使用的CPU内核数量,从而在GridSearchCV和cross_val_score中使用多个内核。你可 以设置 n_jobs=-1 来使用所有可用的内核。你应该知道,
scikit-learn不允许并行操作的嵌套。因此,如果你在模型(比如随机森林)中使用了n_jobs选项,那么就不能在GridSearchCV使用它来搜索这个模型。如果你的数据集和模型都非常大,那么使用多个内核可能会占用大量内存,你应该在并行构建大型模型时监视内存的使用情况。