强化学习DDPG算法

强化学习DDPG算法

前言

因为疫情一直在辗转隔离，没心思学习，索性整理一下学过的东西，记一下学习笔记，就当自我安慰了。推导部分观看了这个B站的学习视频.

DDPG

与DQN不同，DDPG解决问题的能力要比DQN强一些(虽然有一些问题更适合用DQN去解决)。DDPG的一个特点是它可以被用来去解决连续动作空间-连续状态空间(continuous state space and continuous action space)的强化学习问题。比如一个封闭空间的机器人导航的问题，DQN所能给出的机器人动作要么只是“前后左右”这种“概念式”的答案；要么就是把机器人车轮转速离散等分成若干份之后的某一份。而DDPG可以直接给出机器人车轮转速的数值，这是DDPG相对于DQN来讲一个比较有代表性的优点。
我们知道强化学习如果分类的话可以被分成值迭代(value-based)，策略迭代(policy-based)和同时迭代(Actor-Critic)三类，DDPG就属于Actor-Critic大类中的一种。Actor-Critic，顾名思义，就是强化学习的值函数网络(Critic)与策略网络(Actor)同时更新的算法。其中策略网络(Actor)用来给出具体的动作(控制系统就对应控制器输出，小车导航就对应车轮的转速)，值函数网络(Critic)用来评价Actor的输出的好坏程度。
DDPG的全称是Deep Deterministic Policy Gradient。

策略梯度(Policy Gradient)

回想DQN算法，如果所求问题的动作空间是离散的，比如机器人走迷宫(只有上下左右四个选择)，那么对于这个问题，智能体的策略输出就是一个$4\times 1$的向量，其值分别是对应四种选择的概率。但是如果所求问题的动作空间是连续的，比如输出是一个电机的转速，电机转速的连续变化的量，那么这个时候策略网络的输出就不再是一个概率的“分布列”，而是一个连续的概率密度函数。
策略网络(Policy Network)本质上就是强化学习算法的策略$\pi \left(a|s\right)$，只不过用一个神经网络$\pi \left(a|s;\theta \right)$去表示，其中$\theta$是这个神经网络的参数。而策略梯度类算法本质上就是通过改进策略网络(改进网络参数$\theta$)的方式来尽可能地最大化值函数的期望。
$${\pi }^{\ast }=\underset{\pi }{\mathrm{argmax}}{\mathbb{E}}_s{\Sigma }_a\pi \left(a|s;\theta \right)Q_{\pi }\left(s,a\right)$$其中$Q_{\pi }\left(s,a\right)=\mathbb{E}\left[G|S=s,A=a\right]$，$G_t={\Sigma }_{k=0}^{\infty }{\gamma }^k{R}_{t+k}$。

策略梯度的基本思路就是通过对价值函数求导的方式对神经网络的参数$\theta$做梯度上升，从而一步一步地优化策略网络$\pi \left(a|s;\theta \right)$的过程。回想一下DQN(Q-Learning)部分提到过的强化学习的累计奖励(cumulative reward)，状态行为值函数(state-action value function)，和状态值函数的定义(state value function)：
$$\begin{gathered} G_t={\Sigma }_{k=0}^{\infty }{\gamma }^k{R}_{t+k} \\ {Q}_{\pi }\left(s,a\right)=\mathbb{E}\left[G_t|S=s,A=a\right] \\ {V}_{\pi }\left(s\right)={\mathbb{E}}_A\left[Q_{\pi }\left(s,a\right)\right] \end{gathered}$$
策略梯度的目的就是通过优化网络参数($\theta$)的方式来最大化状态值函数的期望。
$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmax}}J\left(\theta \right)=\underset{\theta }{\mathrm{argmax}}\mathbb{E}\left[V_{\pi }\left(s;\theta \right)\right]$$$$\theta \leftarrow \theta +\beta \frac{\partial V_{\pi }\left(s;\theta \right)}{\partial \theta }$$
其中，
$$\begin{array}{rl}\frac{\partial V_{\pi }\left(s;\theta \right)}{\partial \theta }& =\frac{\partial {\Sigma }_a\pi \left(a,s;\theta \right)Q_{\pi }\left(s,a\right)}{\partial \theta }\\ & ={\Sigma }_a\frac{\partial \pi \left(a,s;\theta \right)Q_{\pi }\left(s,a\right)}{\partial \theta }\\ & ={\Sigma }_a\frac{\partial \pi \left(a,s;\theta \right)}{\partial \theta }{Q}_{\pi }\left(s,a\right)(FORM1)\\ & ={\Sigma }_a\pi \left(a,s;\theta \right)\frac{\partial \log \pi \left(a,s;\theta \right)}{\partial \theta }{Q}_{\pi }\left(s,a\right)\\ & ={\mathbb{E}}_{A\sim \pi \left(\cdot |s;\theta \right)}\left[\frac{\partial \log \pi \left(A,s;\theta \right)}{\partial \theta }{Q}_{\pi }\left(s,A\right)\right](FORM2)\end{array}$$
其中，FORM1适用于离散动作空间，FORM2适用于连续动作空间。对于FORM2，直接求是完全不可能的！！里面各种神经网络，log函数，求导，整个函数甚至连一个解析的形式也没有，所以单纯的FORM2那个公式就是个摆设。因此，实际求的时候需要对FORM2里面的策略网络进行蒙特卡洛近似，可以用一次或者多次随机采样的$(s,a)$进行近似，假设某一次随机采样的动作是$\hat{a}$，记
$$f\left(\hat{a},\theta \right)=\frac{\partial \log \pi \left(\hat{a},s;\theta \right)}{\partial \theta }{Q}_{\pi }\left(s,\hat{a}\right)$$根据定义可知，$f\left(\hat{a},\theta \right)$是真值的无偏估计，因此如此近似合理(实际用的时候不见得估计得多好，但是只能这么推，没得办法，因为没办法保证MC采样足够充分)。

$Q_{\pi }\left(s,a\right)$

上一小节看似已经解决了策略梯度问题的求解，但是$Q_{\pi }\left(s,a\right)$一直被忽略了，这部分其实是未知的(很显然是未知的，要是已知的那就不用做了，直接比较大小得到最优策略了，问题就没意义了)。因此，这个函数也是需要用“某种方法”被估计的。有两个办法近似这个$Q_{\pi }\left(s,a\right)$：

方法1：REINFORCE

根据现有的策略网络，生成一条轨迹$s_0,a_0,r_0,s_1,a_1,r_1,\cdots ,s_T,a_T,r_T$(如果是有限时间的就正常采样就行；如果是无限时间的，比如机器人控制系统，那就可以人为指定一个时间截取一下就可以，比如就规定10秒之内必须收敛，那就取10秒的数据作为一条采样轨迹)。然后利用这条轨迹计算出对应地累计奖励$G_t$，将$G_t$作为对Q的估计。

方法2：Actor-Critic

这种方法是用一个神经网络来代替Q函数(理论有点不靠谱，但是实际都这么用)。代替Q函数的神经网络是Critic，策略网络是Actor。Actor-Critic就是DDPG所采用的结构(没错，扣题了^_^)。Actor-Critic是基于策略RL算法与基于值函数的RL算法的结合体。
Actor-Critic中将值函数和策略函数各用一个神经网络表示，也就是说分别用一个神经网络去估计策略的概率分布和状态行为值函数的函数值。
$$\begin{array}{rl}& \pi \left(a|s;\theta \right)\to \pi \left(a|s\right)\\ & q\left(s,a;\omega \right)\to Q_{\pi }\left(s,a\right)\end{array}$$其中$\theta$和$\omega$分别是两个神经网络的网络参数。
策略网络的输入是状态，输出是动作(动作的数值，或者动作的概率分布)；值网络的输入是状态和这个状态对应的动作，输出是一个实数，用来表示与该状态和动作所对应和值函数。
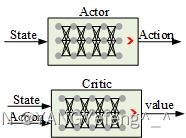策略网络更新的目的是为了让智能体得到值函数最大，值网络更新的目的是为了让Critic的打分更准确，显然最开始两个网络都是瞎猜的，都是在慢慢优化的过程中才逐渐发现规律。下边说两个网络都是如何更新的。

Critic-Q网络

使用TD算法对Q网络进行更新。

Actor-$\pi$网络

使用之前提到过的梯度上升算法更新$\pi$网络。此外，$\pi$网络里面会用到Q网络的数值，那就把上一步的Q网络带进去计算就行(结尾会给出自己实现代码的地址，虽然实现地不太好，但是基本是好用的)。

个人感觉

至此，Actor-Critic方法的全部内容就结束了，这个就是DDPG的工作过程。看到这里还是十分困惑，似乎什么都说了，又似乎什么都没说。看过程感觉非常理所当然，也非常简单，但是往代码实现的方向思考一下，又似乎什么都没说，因为以上提到的东西大多数都是不知道的，而且还有神经网络在里面，个人感觉还是通过代码去体会比较好，网上有很多大神写过的，简洁又好用，可以参考。最后，个人感觉这种算法的理论和实际完全是两个路子，理论上写的公式，早就被实际应用中的各种各样的近似给覆盖掉了。而且为了加强神经网络的稳定性，DDPG也使用了跟DQN一样的估计网络和目标网络的概念，所以实际工作时一共有四个神经网络：Evaluate-Q，Target-Q，Evaluate-$\pi$，Target-$\pi$，然后更新方式可以使用跟DQN一样的硬复制，也可以使用跟神经网络学习参数更新机制一样的软更新。

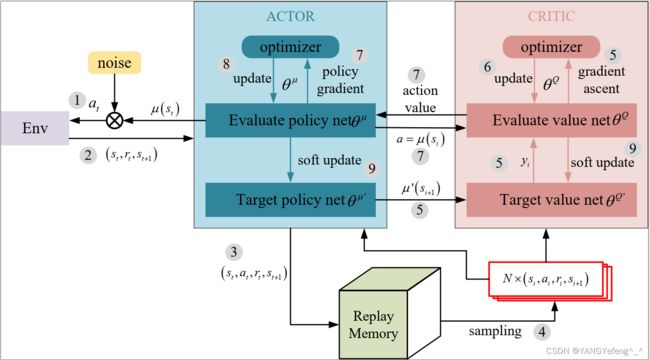
流程图

伪代码

原理图

局限性

貌似很多人认为DDPG几乎全方位地打败了DQN，因为它不仅使用了策略梯度的思想，也把值函数估计的概念引入进去，在Actor-Critic框架下可以实现对任意环境中复杂智能体的学习。
但是实际上DDPG在使用中个人感觉还是有不足的：

1. 比较依赖初始经验池中数据的质量，如果初始经验池中根本就没有成功的回合，或者都是比较相似的回合，那么DDPG学出来的东西可能会很“奇葩”。
2. DDPG中噪声使用的是OU-Noise，具体实现的时候为了简化有时候也用Gaussian-Noise，但是这两种噪声都是在原有输出的基础上附近波动，如果此时真正的最优action离策略网络的原本输出比较远的时候，仅仅通过加噪声的方法很有可能不会让智能体学习地特别充分。
3. 因为action的噪声在学习阶段是一直加在策略网络输出外部的，所以很有可能会遇到学习效果先变好后变差的现象。因为本来action已经接近最优了，但是突然有噪声又把action拉偏了，并且拉偏之后的数据也进入了经验池，然后又碰巧被选中了，就会自然而然地被影射到网络参数中，具体表现就是本来挺好的网络，突然又犯病了…>_<

解决方法除了换算法或者使用诸如TD3等等DDPG的改进之外，比较实用的就是针对具体问题具体分析：修改action噪声的方差、修改网络结构、改变从经验池中挑选数据的策略、有一定的概率输出完全随机的action等等…

以上就是学习笔记，哪里有问题欢迎各位大佬指正。附上代码链接：哈哈哈.