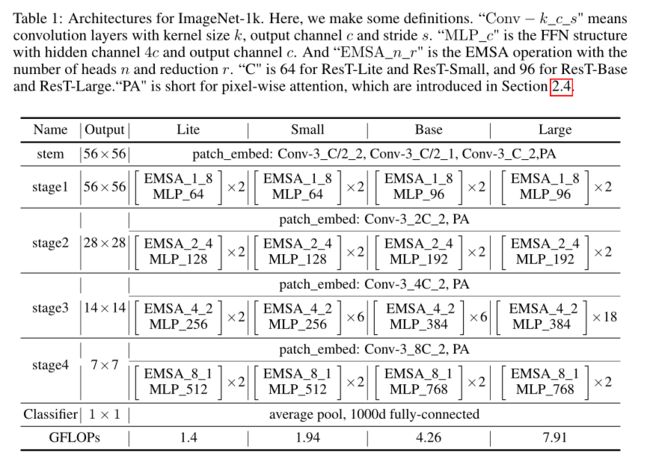
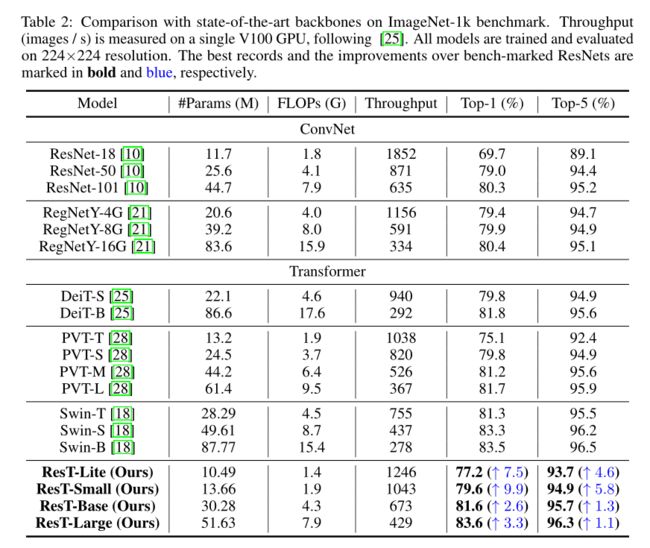
ResT: An Efficient Transformer for Visual Recognition

文章地址: https://arxiv.org/pdf/2105.13677.pdf
code

一、引言

本文提出了一种高效的多尺度视觉Transformer，称为ResT，它能够作为图像识别的通用骨干。与现有的Transformer方法不同，现有的Transformer方法使用标准Transformer块来处理固定分辨率的原始图像，ResT有几个优点:
(1)构建了一个内存高效的多头自注意力，它通过简单的深度卷积来压缩内存，并在保持多头多样性能力的情况下跨注意力头维度投射交互;
(2)将位置编码构造为空间注意力，更灵活，无需插值或微调即可处理任意大小的输入图像;
(3)没有在每个阶段的开始直接进行简单的标记，而是将补丁嵌入设计为在标记映射上进行的重叠卷积操作的堆叠。
与CNN相比，Transformer骨干有很大的发展潜力，但它仍有四个主要的缺点:
(1)由于现有的Transformer骨干网直接从原始输入图像中对patch进行标记化，因此很难提取图像中构成一些基本结构的底层特征(如角和边)。
(2) Transformer块中MSA的内存和计算量与空间或嵌入维度(即通道数量)成二次比例，导致训练和推理的巨大开销。
(3) MSA中的每个头只负责嵌入维数的一个子集，这可能会影响网络的性能，特别是当令牌(每个头)的嵌入维数较短时，查询与键的点积无法构成一个信息函数。
(4)现有Transformer主干中的输入标记和位置编码都是固定规模的，不适合需要密集预测的视觉任务。
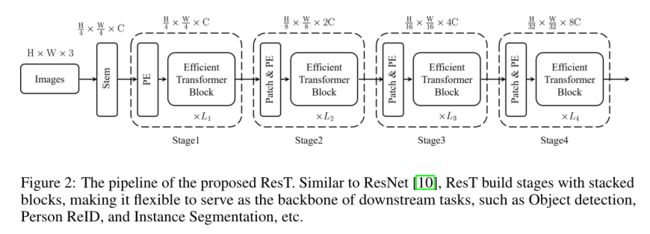
ResT可以解决上述问题。如下图所示，ResT与ResNet的结构完全相同，首先是一个用于提取底层信息并加强局部性的stem模块，然后是构造分层特征图的四个阶段，最后是一个用于分类的head模块。每个阶段包括一个贴片嵌入，一个位置编码模块，以及具有特定空间分辨率和通道维度的多个Transformer块。贴片嵌入模块通过分层扩展通道容量，同时通过重叠卷积操作降低空间分辨率，从而创建多尺度的特征金字塔。
与传统方法只能处理固定尺度的图像不同，本文的位置编码模块被构造为空间注意力，它以输入标记的局部邻域为条件，所提出的方法更加灵活，可以处理任意大小的输入图像，无需插值或微调。此外，为了提高MSA的效率，构建了一个高效的多头自注意力(EMSA)算法，该算法通过简单的重叠深度卷积(Depth-wise Conv2d)显著降低了计算成本。此外，通过在注意头维度上投射交互来弥补每个头的短长度限制，同时保持多个头的多样性能力。

二、ResT

ResT与ResNet共享完全相同的pipeline，即一个用于提取低级信息的主干模块，然后经过四个阶段来捕获多尺度特征映射。每个级由三个组件组成，一个贴片嵌入模块，一个位置编码模块和一组高效Transformer块。具体而言，在每个阶段的开始，采用贴片嵌入模块，降低输入令牌的分辨率，扩大通道维度。融合位置编码模块，抑制位置信息，增强贴片嵌入的特征提取能力。之后，输入令牌被馈送到有效的Transformer块(如下图所示)。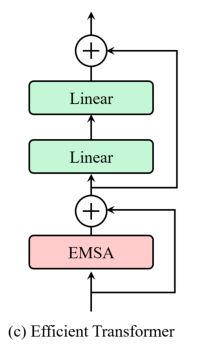

一、Transformer模块的再思考

标准Transformer块由MSA和FFN两个子层组成。每个子层都有一个残差连接。在MSA和FFN之前，应用层归一化(LN)。对于一个令牌输入$x\in R^{n\times d_m}$，其中$n,d_m$分别表示空间维数，通道维数。每个Transformer块的输出是:

MSA:MSA首先通过对输入应用三组投影来获得查询Q、键K和值V，每一组投影由K个线性层(即头部)组成，这些层将$d_m$维输入映射到$d_k$维空间，其中$d_k=d_m/K$是头部维数。为便于描述，设k = 1，则MSA可简化为单头自注意力(single-head self-attention, SA)。令牌序列之间的全局关系可以定义为：

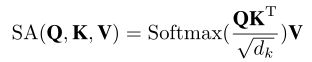
然后将每个头的输出值连接并线性投影以形成最终输出。MSA的计算代价为$O(2d_m{n}^2+4d_m^{2}n)$，根据输入令牌与空间维度或嵌入维度成二次比例。
FFN:FFN用于特征变换和非线性处理。它由两个非线性激活的线性层组成。第一层将输入的嵌入维数从$d_m$扩展到$d_f$，第二层将输入的嵌入维数从$d_f$减小到$d_m$:

其中$W_1\in R^{d_m\times d_f},W_2\in R^{d_f\times d_m}$分别为两个线性层的权值，$b_1\in R^{d_f},b_2\in R^{d_m}$为偏置项，σ(·)为激活函数GELU。在Transformer中，通道尺寸扩大了4倍，即$d_f=4d_m$。FFN的计算代价为$8n{d}_m^2$。
如上所述，MSA有两个缺点:
(1)计算量根据输入令牌按$d_m$或n进行二次扩展，造成大量的训练和推理开销;
(2) MSA中的每个头只负责嵌入维的一个子集，这可能会影响网络的性能，特别是当token嵌入维(每个头)较短时.

二、Efficient Transformer Block

为了解决这些问题，作者提出了一个高效的多头自注意力模块(如下图所示)。

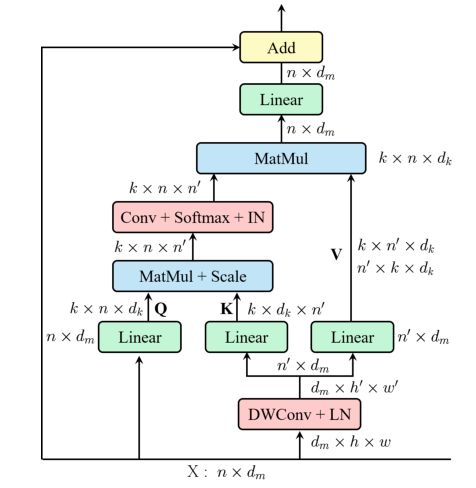
(1)与MSA类似，EMSA首先采用一组投影来获得查询Q。
(2)为了压缩内存，二维输入令牌$x\in R^{n\times d_m}$在空间维度上被重塑为三维(即:$x\in R^{d_m\times h\times w}$)，然后馈入深度卷积运算，将高度和宽度维度降低一个因子s。简单来说，s是由特征图大小或阶段数自适应设置的。内核大小、步幅和填充分别为s + 1、s和s/2。
(3)将空间约简后的新令牌映射为二维令牌映射，即:$x\in R^{d_m\times h/s\times w/s}$, $n^{{}^{\prime }}=h/s\times w/s$。然后，将x馈送给两组投影以获得键K和值V。
(4)之后，采用下式计算查询Q、K和值V的注意力函数。

Conv(·)是一个标准的1 × 1卷积运算，它模拟了不同头之间的相互作用。因此，每个头的注意功能可以依赖于所有的键和查询。然而，这将削弱MSA在不同位置共同处理来自不同表示子集的信息的能力。为了恢复这种多样性能力，我们为点积矩阵(在Softmax之后)添加了一个实例规范化(即IN(·))。

(5)最后，将每个头的输出值进行串联并线性投影，形成最终输出。
EMSA的计算代价为$O(\frac{2d_m{n}^2}{s^2}+2d_m^{2}n(1+\frac{1}{s^2})+d_{m}n\frac{(s+1{)}^2}{s^2}+\frac{k^2{n}^2}{s^2})$，大大低于原来的MSA(假设s > 1)，特别是在较低阶段，s较高时。
此外，在EMSA之后加入FFN来进行特征转换和非线性。每个Efficient Transformer Block的输出为:

三、Patch Embedding

标准Transformer接收一系列令牌嵌入作为输入。以ViT为例，对输入图像$x\in R^{3\times h\times w}$进行patch大小为p × p的分割，将这些patch平化为二维patch，然后映射到大小为c的嵌入，即$x\in R^{n\times c}$，其中$n=hw/p^2$。
然而，这种简单的标记化无法捕获低级特征信息(如边和角)。此外，ViT中标记的长度在不同的块中都是固定的大小，不适合下游视觉任务，如需要多尺度特征映射表示的对象检测和实例分割。
在这里，构建了一个高效的多尺度主干，称为ResT，用于密集预测。如上所述，每个阶段的Efficient Transformer块在相同的尺度上运行，在通道和空间维度上具有相同的分辨率。因此，需要采用贴片嵌入模块逐步扩大通道维度，同时降低整个网络的空间分辨率。
与ResNet类似，采用了stem模块(可以看作是第一个补丁嵌入模块)对高维和宽维都进行了缩窄，缩窄系数为4。为了在参数较少的情况下有效地捕获低特征信息，这里我们介绍了一种简单而有效的方法，即分别将3个3 × 3标准卷积层(均为填充1)与stride 2、stride 1和stride 2进行堆叠。批处理规范化和ReLU激活应用于前两层。
阶段2、阶段3、阶段4采用patch embedding模块对空间维数进行4倍的下采样，通道维数增加2倍。这可以通过步幅2和填充1的标准3 × 3卷积来实现。例如，阶段2的贴片嵌入模块将分辨率从h/4 × w/4 × c改变为h/8 × w/8 × 2c(如下图所示)。

四、Positional Encoding

位置编码对于利用序列的顺序是至关重要的。在ViT中，一组可学习的参数被添加到输入令牌中来编码位置。设$x\in R^{n\times c}$为输入，$\theta \in R^{n\times c}$为位置参数，则编码后的输入可表示为:

但是，位置的长度与输入令牌的长度完全相同，这限制了应用场景。
为了解决这个问题，新的位置编码需要根据输入标记具有可变长度。求和操作很像给输入分配像素权重。设θ与x相关，即θ = GL(x)，其中GL(·)为与c的分组线性运算，则可以表达为下式：

除了上式， θ也可以通过更灵活的空间注意机制得到。在这里，提出了一个简单而有效的空间注意力模块，称为PA(像素注意力)来编码位置。具体来说，PA应用3 × 3深度卷积(填充1)操作来获得像素权重，然后按sigmoid函数σ(·)缩放。PA模块的位置编码可以表示为：

由于每个阶段的输入令牌也是通过卷积运算获得的，因此可以将位置编码嵌入到补丁嵌入模块中。阶段i的整体结构如下所示。请注意PA可以被任何空间注意模块所取代，这使得位置编码在ResT中更加灵活。

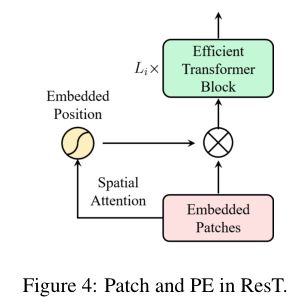
五、整体架构

三、实验

一、分类

使用AdamW优化器训练300个周期，使用余弦衰减学习率调度器和5个周期的线性预热。批处理大小为2048(使用8个GPU，每个GPU 256张图像)，初始学习率为5e-4，权重衰减为0.05，并且使用最大范数为5的梯度归一化。在训练中使用了的大部分增强和正则化策略，包括RandAugment ， Mixup ， Cutmix ， Random erase ， stochastic depth。对于较大的模型，随机深度增强程度增加，即ResT-Lite、Rest-Small、ResT-Base和ResT-Large分别为0.1、0.1、0.2、0.3。对于验证集的测试，首先将输入图像的短边调整为256，并使用224 × 224的中心裁剪进行评估.

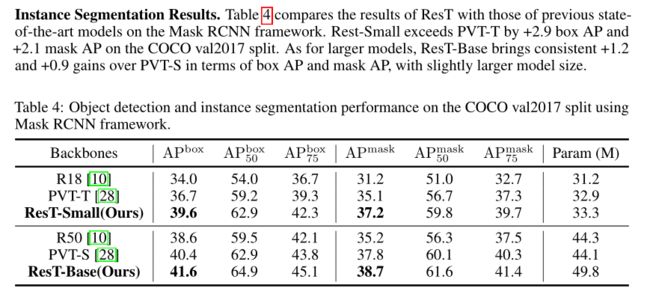
二、目标检测及语义分割

多尺度训练(调整输入的大小，使较短的一侧在480到800之间，而较长的一侧最多为1333)，AdamW优化器(初始学习率为1e-4，权重衰减为0.05，批大小为16)，以及1×调度(12个周期)。
与CNN骨干网不同，骨干网采用归一化后，可直接应用于下游任务。
ResT采用预归一化策略来加速网络收敛，即每个阶段的输出在馈送到FPN之前没有被归一化。在这里，每个阶段的输出(FPN之前)添加了一个层归一化(LN)，类似于Swin。结果在验证分割上报告。

三、消融实验

将输入图像通过随机水平翻转随机裁剪到224 × 224。ResT-Lite的所有架构都使用SGD优化器(权值衰减1e-4，动量0.9)训练100个epoch，从初始学习率0.1 × batch_size/512(线性预热5个epoch)开始，每30个epoch降低10倍。另外，批处理大小为2048(使用8个GPU，每个GPU 256张图像）
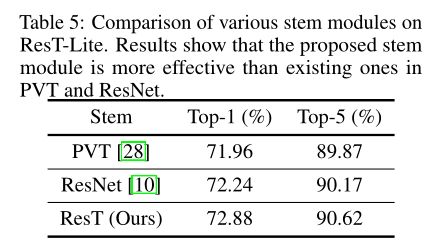
不同类型的stem模块:在这里，测试了三种类型的stem模块:(1)PVT中的第一个补丁嵌入模块，即stride为4且无填充的4 × 4卷积运算;
(2) ResNet中的stem模块，即一个stride 2和padding 3的7 × 7卷积层，后面是一个3 × 3 max-pooling层;
(3)所提出ResT中的stem模块，即3个3 × 3卷积层(均为填充1)，分别为stride 2、stride 1和stride 2。结果如下。ResT中的stem模块比PVT和ResNet更有效:Top-1精度分别提高0.92%和0.64%

EMSA消融研究:采用深度Conv2d来减少MSA的计算量。在这里，提供了具有相同减少步幅的更多策略的比较。结果如下所示。可以看出，与原始的Depth-wise Conv2d相比，平均池化的结果略差(-0.24%)，而Max pooling策略的结果是最差的。由于池化操作不会引入额外的参数，因此，平均池化在实践中可以作为深度Conv2d的替代方法。

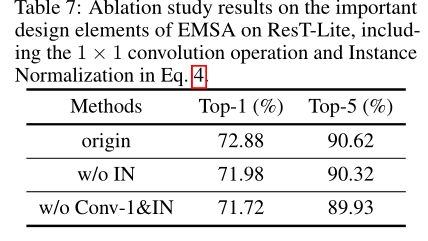
此外，EMSA还在标准MSA的基础上增加了两个重要元素，即1 × 1卷积运算，用于模拟不同头之间的相互作用，实例归一化(Instance Normalization, In)用于恢复不同头的多样性。在这里，验证了这两种设置的有效性。结果如下所示。我们可以看到，在没有IN的情况下，Top-1的准确率下降了0.9%，我们将其归因于不同头之间的多样性被破坏，因为1 × 1的卷积运算使得所有头都集中在所有令牌上。此外，在没有卷积运算和In的情况下，性能下降了1.16%。这说明长序列和多样性的结合对注意力都很重要。

不同类型的位置编码：原始定长可学习参数(LE)、提出的分组线性模式(GL)和PA模式。这些编码在每个阶段的开始时添加/相乘到输入补丁标记。在这里，将提出的GL和PA与LE进行比较，结果如下表所示。可以看到，去掉PA编码后，Top-1的精度从72.88%下降到71.54%，这说明位置编码对于ResT至关重要。LE和GL具有相似的性能，这意味着可以构造可变长度的位置编码。此外，PA模式显著优于GL模式，Top-1精度提高0.84%，表明空间注意力也可以被建模为位置编码。