数学建模——一元线性回归

宋体

一.理论部分

1.什么是一元线性回归 ？

  回归分析是研究相关关系的数学工具。设$Y关于x的回归函数为\mu (x)$，则利用样本$(x_1,Y_1),(x_2,Y_2),...,(x_n,Y_n)$来估计回归函数的问题就称为求$Y$关于$x$的回归问题。当这个回归函数恰好为线性函数(i.e.$\mu (x)=a+bx$)时的回归问题就是一元线性回归问题。

2.一元线性回归模型与基本假设 ？

  一元线性回归模型：$$Y=\mu (x)+\epsilon =a+bx+\epsilon$$
一元线性回归模型的基本假设：
（1）同方差性;即假设对于们一个x的每一个值有Y服从$N(a+bx,{\sigma }^2)$ 。
（2）参数$b\ne 0$（线性假设的显著性检验就要用这个，要是t检验的pvalue<0.5,说明拒绝原假设$H_0:b=0$那么没有就理由认为模型有问题）。

3.怎么求出得到回归函数的估计 ？

用极大似然估计得到的似然函数：$$L(a,b)=\prod C_1{e}^{-C_{2}Q(a,b)}$$,其中C_{1},C_{2}都是大于0的常数.有$Q(a,b)={\sum }_{i=1}^n(y_i-a-b{x}_i)$.通过分析很容易看出来要使得似然函数取最大值是对应的参数$a，b$就是是得$Q(a,b)$取得最小值是对应的参数$a,b$.于是问题转换为极值问题。即可解出参数$a,b$的估计值（求极值点的过程在《概率论与数理统计》第243页）。于是得到回归函数的估计：$\hat{\mu }(x)=\hat{a}+\hat{b}x$回归函数的估计称为回归方程记作：$\hat{y}=\hat{a}+\hat{b}x$.总结一下得到回归函数的估计的方法就是先做一个极大似然估计，然后使得其取极大值。换个角度看$Q(a,b)$实际是残差平方和，直观上看如果这个值越小，那么得到的回归方程对于的直线实际对样本的拟合程度越高。第二种思路就是所谓的最小二乘法。第二部分我们将使用statsmodels提供给的OLS（Ordinary least square）来求解得到模型中的params。

下面我们将手动和利用statsmodels package来判断葡萄酒引用量和心脏病死亡率之间有什么关系。

二.手动实现一元线性回归

先绘制散点图看看酒精摄取量和死亡率之间大致的相关关系，如果接近线性的话就可以用一元线性回归做做看。

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit
import scipy.stats
x=np.array([2.5,3.9,2.9,2.4,2.9,0.8,9.1,0.8,0.7,7.9,
           1.8,1.9,0.8,6.5,1.6,5.8,1.3,1.2,2.7])
y=np.array([211,167,131,191,220,297,71,211,300,107,
           167,266,277,86,207,115,285,199,172])
ax1=plt.subplot(121)
ax1.scatter(x,y,marker='o',color='r')

再用最小二乘法求出参数估计值。这里直接用scipy.optimzie提供的curve_fit做了。这个函数用的是非线性的最小二乘去得到参数估计值。实际上我们这里应该使用线性最小二乘因为模型是参数的线性函数。但是由于curve_fit这个函数的f参数是我们自己来定义的，所以用它来做一元线性回归参数估计也没问题。（numpy提供的polyfit函数同样可以得到参数估计值）。

# 拟合
model_func=lambda x,beta,alpha:beta+alpha*x
f=curve_fit(model_func,x,y)
print('参数估计值:',f[0])  #  [266.16625514 -23.95058865]
# 样本的的估计值
func=lambda x:266.16625514-23.95058865*x
new_y=func(x)
ax2=plt.subplot(122)
ax2.plot(x,new_y,label='fitting line');ax2.scatter(x,y,color='cyan',label='sample point')
ax2.legend(loc='best')
plt.suptitle('Univariate linear regression')

下面我们做（1）线性假设的显著性检验（就是T检验b是否为0，套结论就好了。详细推导在《概率论与数理统计》第249页）。（2）求解$R^2$，这个参数反映出有多少数据点落到回归曲线上，显然越接近1那么回归直线越好。（3）F-statisic,这个还是做了f检验来检验我们b是不是为0.其实没必要再做了。（i.e. 1,3选一个做好了）

xmean,ymean=np.mean(x),np.mean(y)
lxy=np.sum((x-xmean)*(y-ymean))
lxx=np.sum((x-xmean)**2)
lyy=np.sum((y-ymean)**2)
# Sum of squares of total variation，Sum of squares of the regression，Sum of Squares for Error
SST=lyy
SSR=np.sum((new_y-ymean)**2)
SSE=np.sum((y-new_y)**2)

输出结果分析：看p值就好了，<0.5说明原假设被拒绝，就是说b不为0.这是在预期内的，于是没有理由有认为模型有问题。而Rsqared即$R^2$=0.7213,说明有72%左右得到点是落到回归直线上的，那么这个回归直线是比较好的。就是说葡萄酒用量和心脏病死亡率之间的关联是很显著的。所以适当饮酒有益健康LOL…

三.使用Python的statsmodels package来完成

# use statsmodels can be easier
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
# 样本
x=np.array([2.5,3.9,2.9,2.4,2.9,0.8,9.1,0.8,0.7,7.9,
           1.8,1.9,0.8,6.5,1.6,5.8,1.3,1.2,2.7])
y=np.array([211,167,131,191,220,297,71,211,300,107,
           167,266,277,86,207,115,285,199,172])
# 因为我们的模型是a+bx，而OLS模型默认没有截距项，使用add_constant添加截距项
X=sm.add_constant(x)
# 拟合模型并获取总结表.
# OLS即ordinary least square 是一种找到是得总变差最小的参数的算法
result=sm.OLS(y,X).fit()
print(result.summary())

绘制一下回归直线

# 打印下参数估计值
print(result.params)  #[266.1663,23.9506]
# 回归方程
new_y=(lambda x:266.1663-23.9506*x)(x)
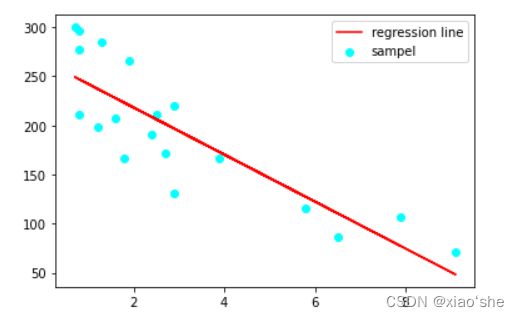
# 绘图
plt.plot(x,new_y,label='regression line',color='r')
plt.scatter(x,y,label='sampel',color='cyan')
plt.legend(loc='best')