《算法导论》读书笔记之第15章 动态规划—最长公共子序列
1、基本概念
一个给定序列的子序列就是该给定序列中去掉零个或者多个元素的序列。形式化来讲就是:给定一个序列X={x1,x2,……,xm},另外一个序列Z={z1、z2、……,zk},如果存在X的一个严格递增小标序列<i1,i2……,ik>,使得对所有j=1,2,……k,有xij = zj,则Z是X的子序列。例如:Z={B,C,D,B}是X={A,B,C,B,D,A,B}的一个子序列,相应的小标为<2,3,5,7>。从定义可以看出子序列直接的元素不一定是相邻的。
公共子序列:给定两个序列X和Y,如果Z既是X的一个子序列又是Y的一个子序列,则称序列Z是X和Y的公共子序列。例如:X={A,B,C,B,D,A,B},Y={B,D,C,A,B,A},则序列{B,C,A}是X和Y的一个公共子序列,但不不是最长公共子序列。
最长公共子序列(LCS)问题描述:给定两个序列X={x1,x2,……,xm}和Y={y1,y2,……,yn},找出X和Y的最长公共子序列。
2、动态规划解决过程
1)描述一个最长公共子序列
如果序列比较短,可以采用蛮力法枚举出X的所有子序列,然后检查是否是Y的子序列,并记录所发现的最长子序列。如果序列比较长,这种方法需要指数级时间,不切实际。
LCS的最优子结构定理:设X={x1,x2,……,xm}和Y={y1,y2,……,yn}为两个序列,并设Z={z1、z2、……,zk}为X和Y的任意一个LCS,则:
(1)如果xm=yn,那么zk=xm=yn,而且Zk-1是Xm-1和Yn-1的一个LCS。
(2)如果xm≠yn,那么zk≠xm蕴含Z是是Xm-1和Yn的一个LCS。
(3)如果xm≠yn,那么zk≠yn蕴含Z是是Xm和Yn-1的一个LCS。
定理说明两个序列的一个LCS也包含两个序列的前缀的一个LCS,即LCS问题具有最优子结构性质。
2)一个递归解
根据LCS的子结构可知,要找序列X和Y的LCS,根据xm与yn是否相等进行判断的,如果xm=yn则产生一个子问题,否则产生两个子问题。设C[i,j]为序列Xi和Yj的一个LCS的长度。如果i=0或者j=0,即一个序列的长度为0,则LCS的长度为0。LCS问题的最优子结构的递归式如下所示:

3)计算LCS的长度
采用动态规划自底向上计算解。书中给出了求解过程LCS_LENGTH,以两个序列为输入。将计算序列的长度保存到一个二维数组C[M][N]中,另外引入一个二维数组B[M][N]用来保存最优解的构造过程。M和N分别表示两个序列的长度。该过程的伪代码如下所示:
1 LCS_LENGTH(X,Y) 2 m = length(X); 3 n = length(Y); 4 for i = 1 to m 5 c[i][0] = 0; 6 for j=1 to n 7 c[0][j] = 0; 8 for i=1 to m 9 for j=1 to n 10 if x[i] = y[j] 11 then c[i][j] = c[i-1][j-1]+1; 12 b[i][j] = '\';
13 else if c[i-1][j] >= c[i][j-1] 14 then c[i][j] = c[i-1][j]; 15 b[i][j] = '|'; 16 else
17 c[i][j] = c[i][j-1]; 18 b[i][j] = '-'; 19 return c and b
由伪代码可以看出LCS_LENGTH运行时间为O(mn)。
4)构造一个LCS
根据第三步中保存的表b构建一个LCS序列。从b[m][n]开始,当遇到'\'时,表示xi=yj,是LCS中的一个元素。通过递归即可求出LCS的序列元素。书中给出了伪代码如下所示:
1 PRINT_LCS(b,X,i,j) 2 if i==0 or j==0
3 then return
4 if b[i][j] == '\'
5 then PRINT_LCS(b,X,i-1,j-1) 6 print X[i] 7 else if b[i][j] == '|'
8 then PRINT_LCS(b,X,i-1,j) 9 else PRINT_LSC(b,X,i,j-1)
3、编程实现
现在采用C++语言实现上述过程,例如有两个序列X={A,B,C,B,D,A,B}和Y={B,D,C,A,B,A},求其最长公共子序列Z。完整程序如下所示:
1 #include <iostream> 2 using namespace std; 3 #define X_LEN 7 4 #define Y_LEN 6 5 #define EQUAL 0 6 #define UP 1 7 #define LEVEL 2 8 void lcs_length(char* X,char* Y,int c[X_LEN+1][Y_LEN+1],int b[X_LEN+1][Y_LEN+1]); 9 void print_lcs(int b[X_LEN+1][Y_LEN+1],char *X,int i,int j); 10 11 int main() 12 { 13 char X[X_LEN+1] = {' ','A','B','C','B','D','A','B'}; 14 char Y[Y_LEN+1] = {' ','B','D','C','A','B','A'}; 15 int c[X_LEN+1][Y_LEN+1]={0}; 16 int b[X_LEN+1][Y_LEN+1] = {0}; 17 int i,j; 18 lcs_length(X,Y,c,b); 19 for(i=0;i<=X_LEN;i++) 20 { 21 for(j=0;j<=Y_LEN;j++) 22 cout<<c[i][j]<<" "; 23 cout<<endl; 24 } 25 cout<<"The length of LCS is: "<<c[X_LEN][Y_LEN]<<endl; 26 cout<<"The longest common subsequence between X and y is: "<<endl; 27 print_lcs(b,X,X_LEN,Y_LEN); 28 return 0; 29 } 30 //采用动态规划方法自底向上的进行计算,寻找最优解 31 void lcs_length(char* X,char* Y,int c[X_LEN+1][Y_LEN+1],int b[X_LEN+1][Y_LEN+1]) 32 { 33 int i,j; 34 //设置边界条件,即i=0或者j=0 35 for(i=0;i<X_LEN;i++) 36 c[i][0] = 0; 37 for(j=0;j<Y_LEN;j++) 38 c[0][j] = 0; 39 for(i=1;i<=X_LEN;i++) 40 for(j=1;j<=Y_LEN;j++) 41 { 42 if(X[i] == Y[j]) //满足递归公式第二条 43 { 44 c[i][j] = c[i-1][j-1]+1; 45 b[i][j] = EQUAL ; 46 } 47 else if(c[i-1][j] >= c[i][j-1]) //递归公式第三条 48 { 49 c[i][j] = c[i-1][j]; 50 b[i][j] = UP; 51 } 52 else 53 { 54 c[i][j] = c[i][j-1]; 55 b[i][j] = LEVEL; 56 } 57 } 58 } 59 void print_lcs(int b[X_LEN+1][Y_LEN+1],char *X,int i,int j) 60 { 61 if(i==0 || j==0) 62 return; 63 if(b[i][j] == EQUAL) 64 { 65 print_lcs(b,X,i-1,j-1); 66 cout<<X[i]<<" "; 67 } 68 else 69 if(b[i][j] == UP) 70 print_lcs(b,X,i-1,j); 71 else 72 print_lcs(b,X,i,j-1); 73 }
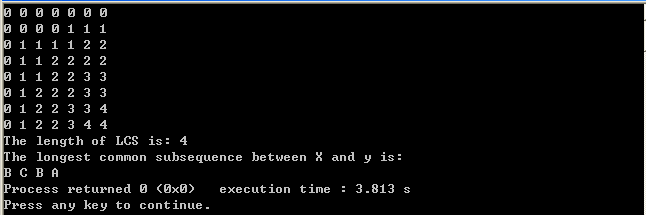
程序测试结果如下所示: