数据结构之队列(链式队列)的基本操作与实现
这篇文章的末尾有完整的实现代码,书写不易,转载请附上本文章链接。
目录
一、链式队列的概念
二、链式队列的基本操作
(1)、链队的初始化
(2)、判断链队是否为空
(3)、求链队列的长度
(4)、入队操作
(5)、求链队首元素
(6)、出队操作
(7)、主函数
(8)、运行结果
(9)、完整代码
一、链式队列的概念
何为链式队列,想到链式队列大家应该都会想到顺序表的单链表的基本操作,我们来对比一下:单链表是用一个头指针或者是尾指针来实现元素的插入和删除等,即头插法和尾插法。而链式队列呢,我们都知道队列是一个在队首进行出队再队尾进行入队,而不是在一段完成任务,所以我们这里就需要两个指针分别指向队列的头front和尾rear,他们两个各司其职,当要进行出队操作时,头指针front说了算,当要进行入队操作时,尾指针rear说了算。
约束条件:我们把头指针指向队列中第一个元素的前一个位置,它里面不存东西,他只是一个标记,标记着它指向了一个队列,通过它可以找到这个队列,就像是单链表的头插法;而尾指针指向队列的最后一个元素。
二、链式队列的基本操作
熟悉了链式队列的概念之后,我们就可定义链式队列的基本操作了,操作并不局限于我说的这些,根据实际情况,定义所需的操作。
(1)、链队的初始化
(2)、判断链队是否为空
(3)、求链队列的长度
(4)、入队操作
(5)、出队操作
(6)、求链队首元素 ,(我们也可以求链队的队尾元素)
三、基本操作的具体实现步骤
首先声明一个队列节点结构体,结构体里包括这个节点的指针域next和数据域data。再声明一个队列结构体,包括指向这个队列的头指针front和尾指针rear。
#include
#include
typedef int Elemtype;
//声明一个结构体来表示节点
typedef struct Node
{
Elemtype data; //节点数据域
struct Node * next; //节点指针域
}QueueNode;
//声明一个结构体来定义上面这个结构体的两个指针
typedef struct
{
QueueNode *front,*rear;//分别指向队首和队尾的指针
}LinkQueue; (1)、链队的初始化
当前的链队是一个空的队,所以头指针尾指针和节点指针都指向同一个地方,指向空。
//首先进行初始化
void Init(LinkQueue *s)
{
QueueNode * p;
p=(QueueNode*)malloc(sizeof(QueueNode));//为指向节点的指针分配空间
p->next=NULL;
s->front=s->rear=p;
}(2)、判断链队是否为空
因为我们在初始化的时候定义的头指针和尾指针指向同一个位置标记为空,所以我们就判断是否它们指向同一个地方。
//判断队列是否为空,为空返回真1,不为空返回假0
int Empty(LinkQueue s)
{
//队空的条件是头指针和尾指针指向相同的地方
if(s.front==s.rear)
{
return 1;
}
return 0;
}(3)、求链队列的长度
我们就声名一个临时的节点类型的指针变量p,让它指向链队的第一个节点,在声明一个变量记录长度,当p指向的节点不为空时,就让长度增加一,同时,指针p也向后移动一个位置。
//求队列长度
int GetLength(LinkQueue s)
{
//声明一个节点类型的指针
QueueNode *p;
//让p指向队列的头指针
p=s.front;
//声明一个变量用来记录队列当前长度
int length=0;
while(p->next)//当指针p所指的节点不为空时执行循环体
{
length++;
p=p->next;
}
return length;//返回当前队列的长度
}(4)、入队操作
我们在文章开头说过,入队操作由队尾指针rear决定。我们声明一个节点类型的指针变量p,为它分配空间,然后将要入队的元素赋值给它,然后将rear指针指向这个节点,之后rear指针向后移动一位。这和顺序链表的尾插法的操作很类似,大家可以对比一下,思想是一样的。
//入队操作
void Add(LinkQueue *s,Elemtype x)
{
//声明一个节点类型的指针变量用来存储要入队的元素
QueueNode *p;
p=(QueueNode*)malloc(sizeof(QueueNode));
if(!p){
printf("内存分配失败\n\n");
return;
}
p->data=x; //指针指向的节点的数据域存放x
p->next=NULL; //指针指向的节点的指针域置为空
s->rear->next=p; //将队列的尾指针的指针域next指向指针p所指的节点
s->rear=p; //将队列的尾指针向后移一位,指向刚入队的节点的位置
}(5)、求链队首元素
我们这里只求了队首元素,没有求队尾元素。在求队首元素时,我们要判断一下队是否为空队列。如果不为空了我们再进行求队首元素的操作。直接返回头指针front指向的第一个元素的值。
//获取队首元素
Elemtype GetTop(LinkQueue s)
{
//首先判断队列是否为空
if(Empty(s))
{
printf("队列为空,无法获取队首元素\n\n");
return 0;
}
return s.front->next->data;//不为空的话就返回队首指针指向的第一个元素的数据域
}(6)、出队操作
出队操作由队首指针front决定。我们要判断一下队是否为空队列。我们声明一个节点类型的指针变量p,将它指向队首元素的第一个节点的位置。然后让e记录下当前出队的元素的值。将队首指针指向第一个节点的下一个节点。这和顺序链表的头插法的删除操作很类似。要记着释放指向出队节点的指针。
//出队操作
void Del(LinkQueue *s,Elemtype *e)
{
//先判断队列是否为空
if(Empty(*s))
{
printf("当前队列为空,无法执行出队操作\n\n");
return;
}
//用临时变量保存出队的元素
QueueNode *p;
p=s->front->next;
if(p==s->rear) //如果p指向了队尾节点
{
s->front=s->rear; //那么删除之后队首指针和尾指针指向同一个位置
}
*e=p->data;
s->front->next=p->next;//将队首指针指向第一个节点的下一个节点。
free(p);
}(7)、主函数
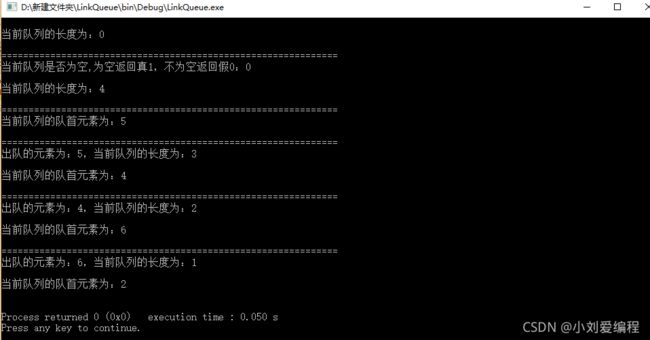
int main()
{
//声明一个节点类型的变量
Elemtype e;
//声明一个顺序队名字为s
LinkQueue s;
//对这个顺序队进行初始化
Init(&s);
printf("==============================================================\n");
printf("当前队列是否为空,为空返回真1,不为空返回假0:%d\n\n",Empty(s));
printf("当前队列的长度为:%d\n\n",GetLength(s));
//执行入队操作
Add(&s,5);
Add(&s,4);
Add(&s,6);
Add(&s,2);
printf("==============================================================\n");
printf("当前队列是否为空,为空返回真1,不为空返回假0:%d\n\n",Empty(s));
printf("当前队列的长度为:%d\n\n",GetLength(s));
//获取当前队首元素
printf("==============================================================\n");
e=GetTop(s);
if(e){
printf("当前队列的队首元素为:%d\n\n",e);
}
//执行出队操作
printf("==============================================================\n");
Del(&s,&e);
printf("出队的元素为:%d,当前队列的长度为:%d\n\n",e,GetLength(s));
//获取当前队首元素
e=GetTop(s);
if(e){
printf("当前队列的队首元素为:%d\n\n",e);
}
//再执行一次出队操作
printf("==============================================================\n");
Del(&s,&e);
printf("出队的元素为:%d,当前队列的长度为:%d\n\n",e,GetLength(s));
//获取当前队首元素
e=GetTop(s);
if(e){
printf("当前队列的队首元素为:%d\n\n",e);
}
//再执行一次出队操作
printf("==============================================================\n");
Del(&s,&e);
printf("出队的元素为:%d,当前队列的长度为:%d\n\n",e,GetLength(s));
//获取当前队首元素
e=GetTop(s);
if(e){
printf("当前队列的队首元素为:%d\n\n",e);
}
return 0;
}(8)、运行结果
(9)、完整代码
#include
#include
typedef int Elemtype;
//声明一个结构体来表示节点
typedef struct Node
{
Elemtype data; //节点数据域
struct Node * next; //节点指针域
}QueueNode;
//声明一个结构体来定义上面这个结构体的两个指针
typedef struct
{
QueueNode *front,*rear;//分别指向队首和队尾的指针
}LinkQueue;
//首先进行初始化
void Init(LinkQueue *s)
{
QueueNode * p;
p=(QueueNode*)malloc(sizeof(QueueNode));
p->next=NULL;
s->front=s->rear=p;
}
//判断队列是否为空,为空返回真1,不为空返回假0
int Empty(LinkQueue s)
{
//队空的条件是头指针和尾指针指向相同的地方
if(s.front==s.rear)
{
return 1;
}
return 0;
}
//求队列长度
int GetLength(LinkQueue s)
{
//声明一个节点类型的指针
QueueNode *p;
//让p指向队列的头指针
p=s.front;
//声明一个变量用来记录队列当前长度
int length=0;
while(p->next)//当指针p所指的节点不为空时执行循环体
{
length++;
p=p->next;
}
return length;//返回当前队列的长度
}
//入队操作
void Add(LinkQueue *s,Elemtype x)
{
//声明一个节点类型的指针变量用来存储要入队的元素
QueueNode *p;
p=(QueueNode*)malloc(sizeof(QueueNode));
if(!p){
printf("内存分配失败\n\n");
return;
}
p->data=x; //指针指向的节点的数据域存放x
p->next=NULL; //指针指向的节点的指针域置为空
s->rear->next=p; //将队列的尾指针的指针域next指向指针p所指的节点
s->rear=p; //将队列的尾指针向后移一位,指向刚入队的节点的位置
}
//获取队首元素
Elemtype GetTop(LinkQueue s)
{
//首先判断队列是否为空
if(Empty(s))
{
printf("队列为空,无法获取队首元素\n\n");
return 0;
}
return s.front->next->data;//不为空的话就返回队首指针指向的第一个元素的数据域
}
//出队操作
void Del(LinkQueue *s,Elemtype *e)
{
//先判断队列是否为空
if(Empty(*s))
{
printf("当前队列为空,无法执行出队操作\n\n");
return;
}
//用临时变量保存出队的元素
QueueNode *p;
p=s->front->next;
if(p==s->rear)
{
s->front=s->rear;
}
*e=p->data;
s->front->next=p->next;
free(p);
}
int main()
{
//声明一个节点类型的变量
Elemtype e;
//声明一个顺序队名字为s
LinkQueue s;
//对这个顺序队进行初始化
Init(&s);
printf("==============================================================\n");
printf("当前队列是否为空,为空返回真1,不为空返回假0:%d\n\n",Empty(s));
printf("当前队列的长度为:%d\n\n",GetLength(s));
//执行入队操作
Add(&s,5);
Add(&s,4);
Add(&s,6);
Add(&s,2);
printf("==============================================================\n");
printf("当前队列是否为空,为空返回真1,不为空返回假0:%d\n\n",Empty(s));
printf("当前队列的长度为:%d\n\n",GetLength(s));
//获取当前队首元素
printf("==============================================================\n");
e=GetTop(s);
if(e){
printf("当前队列的队首元素为:%d\n\n",e);
}
//执行出队操作
printf("==============================================================\n");
Del(&s,&e);
printf("出队的元素为:%d,当前队列的长度为:%d\n\n",e,GetLength(s));
//获取当前队首元素
e=GetTop(s);
if(e){
printf("当前队列的队首元素为:%d\n\n",e);
}
//再执行一次出队操作
printf("==============================================================\n");
Del(&s,&e);
printf("出队的元素为:%d,当前队列的长度为:%d\n\n",e,GetLength(s));
//获取当前队首元素
e=GetTop(s);
if(e){
printf("当前队列的队首元素为:%d\n\n",e);
}
//再执行一次出队操作
printf("==============================================================\n");
Del(&s,&e);
printf("出队的元素为:%d,当前队列的长度为:%d\n\n",e,GetLength(s));
//获取当前队首元素
e=GetTop(s);
if(e){
printf("当前队列的队首元素为:%d\n\n",e);
}
return 0;
}
总结:学到这里对比一下顺序表,栈,队,有很多相同之处,各自又拥有自己的独特之处,结合我的前几篇关于数据结构的文章大家可以自己对比一下。
请尊重劳动成果,转载请注明原文链接和出处。