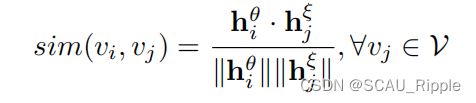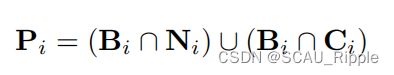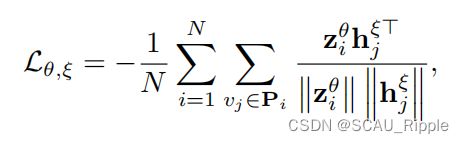论文阅读“Augmentation-Free Self-Supervised Learning on Graphs”(AAAI 2022)

论文标题

Augmentation-Free Self-Supervised Learning on Graphs

论文作者、链接

作者：Lee, Namkyeong and Lee, Junseok and Park, Chanyoung

链接：https://arxiv.org/pdf/2112.02472.pdf

代码：GitHub - Namkyeong/AFGRL: The official source code for "Augmentation-Free Self-Supervised Learning on Graphs" ( https://arxiv.org/abs/2112.02472 )

---

Introduction逻辑

 自监督学习——自监督中的对比学习——图片中的对比学习——图对比学习——模型表现依靠数据增广的选择，又收到数据增广的超参的影响——本文方法

论文动机&现有工作存在的问题

现有的图对比学习以及图像的对比学习方法往往依赖于数据增广，模型性能直接与选用的数据增广挂钩。

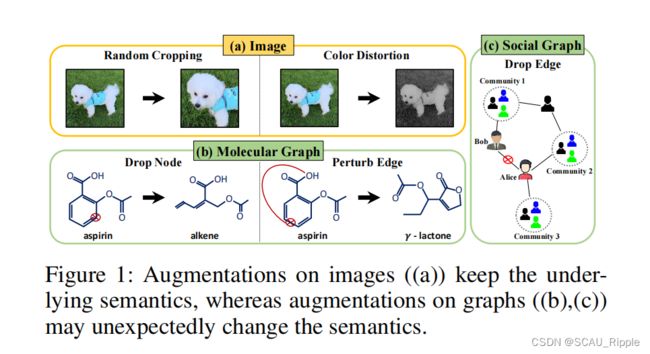
在image上使用的数据增广手法不一定在graph上适用

需要大量负样本

论文核心创新点

不需要数据增广也不需要负样本对

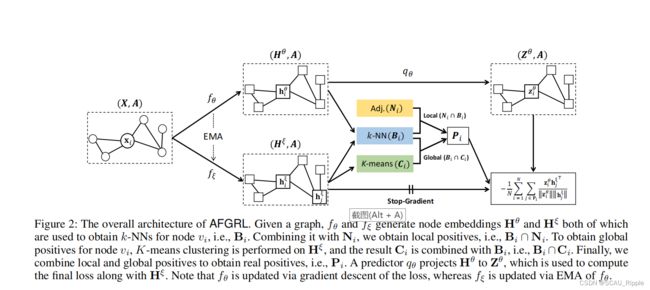
比起生成两个随机的数据增广视图并希望他们保留原视图的语义信息，本文方法将原图视为一个视图，并通过发现原始图中的每个节点，在表示空间中通过k-近邻(k-NN)搜索可以作为正样本的节点，来生成另一个视图。对于这两个语义相关的视图，目标是预测第一个视图中的每个节点在第二个视图中的正节点的潜在表示。然而，基于k-NN搜索的简单地选择正样本来生成另一个视图仍然会改变原始图的语义。

于是本文提出了另一种机制，从k-NN搜索发现的样本中过滤出假阳性样本。两个情况下是正样本：（1）在邻接矩阵中，这是一个目标节点的相邻节点（局部视角）,或（2）与目标节点同属一个簇（全局视角）。

---

相关工作

对比图学习方法：存在样本偏差；需要大量负样本

图增广：暂时没有一种通用的效果好的图增广方法，现有方法会导致（1）改变原图的语义信息（2）要求特定域的知识

---

预备知识

定义一个图，其中表示顶点集合，表示边集。与特征矩阵和邻接矩阵，其中

 目标任务：对于给定的图的，学习一个编码器去生成节点嵌入，其中D远小于F

 本文前置工作BYOL

---

论文方法

通过数据增广生成可选视图 

BGRL 是最近提出的一种学习节点表示的完全非对比方法，受益于BYOL框架，不利用负样本进行学习。BGRL通过手动增强生成一个图的两种不同视图，即节点特征掩蔽和边缘掩蔽。然后两个编码器，即在线和目标编码器，生成给定图形的增强视图对应的嵌入，并使得两个生成的嵌入彼此接近。为了防止表示崩溃成平凡的解，BGRL引入了一种对称打破技术。同样值得注意的是，BGRL有意地考虑了简单的增强技术，以验证在图上应用完全非对比方案的好处。

针对图的增广方法的局限性

在不使用负样本的情况下，本文作者观察到学习到的节点表示的质量依赖于增广方案的选择，并且针对不同的下游任务要设置不同的超参。

基于无数据增广的GRL方法Augmentation-Free GRL (AFGRL)

对于图中的每一个节点，根据两个编码器（即在线编码器和目标编码器）学习到的节点表示，发现可以作为正样本的节点。这两个编码器根据原始图谱的邻接矩阵和特征矩阵初始化，并且计算在线、目标表示：，其中的第行，即，是第个节点的特征表示。对一个给定的查询节点 ，计算其与其他所有节点的余弦相似性：

 即计算在线和目标的特征表示的余弦相似性。给定了相似性信息后，计算每一个节点的K-近邻的节点集，该集合记作，可以视为节点的正样本集。我们希望这K个最近邻点在特征空间属于同一个语义类。

尽管可以作为节点的一个合理的正样本候选集合，但（1）它本身是有噪声的，因为我们没有利用任何标签信息，即包含与查询节点没有语义关联的样本。此外，如果只考虑表示空间中的最近邻居，可能会忽略（2）图的结构信息，即关系归纳偏差，也可能忽略（3）图的全局语义信息。

为了解决这些局限性，本文引入了一种机制，从K-NN搜索发现的样本中过滤出假阳性，同时也捕获图的局部结构信息和全局语义。

捕获局部结构信息

 上文中提到希望K-NN的近邻点都同属于一个类，为了验证预期是否成立，对两个数据集进行分析，即如下图所示，使用的Amazon Computers和WikiCS数据集

 首先，从随机初始化的两层GCN中获得节点嵌入，即，然后对嵌入进行k-NN搜索。然后对每一个点计算该点与其近邻所属于同一个标签的概率。在上图中，我们观察到，虽然在只考虑少量邻居时，例如k = 4，刚刚的同属一个标签的概率很高，但在两个数据集中，随着k的增大，该比例下降。这意味着，期望在一定程度上是成立的，但仍然存在噪声。

 本文为了去除k-NN中的假阳性样本点，利用了节点的局部信息。对于每一个节点，其邻接点应倾向于与其使用同一个标签。在图3中，在两个数据集中，相邻节点与查询节点具有相同标签的比例(Adj)约为70%，这证明了平滑性假设的有效性。因此，为了捕捉平滑性假设中反映的关系诱导偏差，在滤除噪声最近邻居的假阳性的同时，我们计算最近邻居和相邻节点之间的交集，即，将新的集合成为的剧本正样本集。在图3中，局部正样本集随着k值增加一直保持高相关度。

捕获全局的语义信息  

本文通过聚类来获得全局的语义信息。目的是发现与某个节点共享全局语义信息的不相邻节点。作者认为，语义相似但不共享边缘的实例可以通过全局视角的集群发现。

对目标特征做K-means将节点分成K个簇即，以及代表的簇分布，其中。然后对于与同属一个簇的节点集合作为全局下的语义相似点。最后，我们得到了最近邻点与语义相似节点在全局视角下的交集，并这个并集记为的全局正样本集。也就是说，在的最近邻居中，同时与属于同一簇的节点被认为是全局正邻居点。

因为K-means对初始化的位置敏感，于是，本文做M次的K-means，得到M组簇集合即，其中是第次的聚类结果。然后定义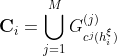，其中代表的第次簇分布。

目标函数

 同时考虑局部和全局信息，定义对于节点的真实正样本集为：

所以全局的目标是减小对其真实正样本集中的点的余弦距离：

 其中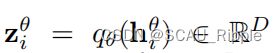，是在线嵌入的预测值，并且是预测网络。与BYOL一样，在线网络根据梯度下降更新，目标网络根据在线网络动量更新。

---

消融实验设计

模型中每一个组件删去的消融

超参消融

---

一句话总结

首先不依赖数据增广，其次构建真实样本集。

---

论文好句摘抄（个人向）

（1）Specififi- cally, contrastive methods, which are at the core of self-supervised learning paradigm, aim to build effective representation by pulling semantically similar (positive) pairs to gether and pushing dissimilar (negative) pairs apart.

（2）Although self-supervised contrastive methods have been shown to be effective on various graph-related tasks, they pay little attention to the inherent distinction between images and graphs: while augmentation is well defifined on images, it may behave arbitrarily on graphs.