离线强化学习(Offline RL)系列5: (模型参数) 离线强化学习中的超参数选择(Offline Hyperparameters Selection)

论文信息： Tom Le Paine, Cosmin Paduraru, Andrea Michi, Caglar Gulcehre, Konrad Zolna, Alexander Novikov, Ziyu Wang, Nando de Freitas: “Hyperparameter Selection for Offline Reinforcement Learning”, 2020; arXiv:2007.09055.

本文由DeepMind和Google合作，由Tom Le Paine以第一作者完成并被NeurIPS2021 接收为Accept (Poster)，评审意见是：The manuscript examines the question of how to improve policy selection in the off-line RL setting. Typically offline policy selection is approached via off-policy evaluation (OPE), aimed at estimating the expected return of candidate policies. OPE is itself a difficult problem that typical requires hyperparameter tuning and selection itself. The paper develops moves closer to a hyperparameter-free method and demonstrates the effectiveness of the algorithm in the context of standardized offline datasets (e.g. RLUnplugged for Atari). The algorithm for policy selection is built using insights from the recently published Batch Value-Function Tournament (BVFT) approach to estimating the best value function from among a set of candidates. They make comparisons to well developed OPE style methods such as fitted Q-evaluation and show clear advantages in data efficiency and the policy selection. The manuscript examines applying the approach to a wide range of settings (from Atari to continuous control) and to a range of policies produced by a variety of algorithms. The ideas, theory, and experiments are well motivated by the text. Taken together, the manuscript provides a promising look at a fundamental and open problem in RL.

摘要: 离线强化学习的数据集、数据集的特征、采样复杂性以及算法实现在之前的博客中已经阐述了很多，此外，对算法效率还有一个非常重要的影响特性：超参数的选择，本文作者就该过程进行了阐述，并提出了使用3种指标衡量选择效果，最后基于FQE算法实验，通过与常见的CRR等算法进行对比。

1. 问题描述

1.1 监督学习超参数选择与调优

在监督学习中，常见的学习率、网络结构等超参数对模型的收敛都有非常大的影响，Google了一下，在监督学习领域目前比较常见的叫法不是hyperparameter selection， 普遍是hyperparameter tuning/optimization， 典型的优化过程定义了可能的超参数集以及针对该特定问题要最大化或最小化的度量， 实践中遵循以下步骤：

（1）将数据集拆分为训练和测试子集
（2）重复优化循环固定次数或直到满足条件：

• 选择一组新的模型超参数
• 使用选定的超参数集在训练子集上训练模型
• 将模型应用于测试子集并生成相应的预测
• 使用针对手头问题的适当评分指标评估测试预测，例如准确度或平均绝对误差。 存储对应于所选超参数集的度量值

（3）比较所有度量值并选择产生最佳度量值的超参数集

而常见的方法主要包括以下四种

• Grid search
• Random search
• Hill climbing
• Bayesian optimization

比如针对函数 $f(x)=sin(x/2)+0.5\cdot sin(2\cdot x)+0.25\cdot cos(4.5\cdot x)$ 问题，求解过程如图：

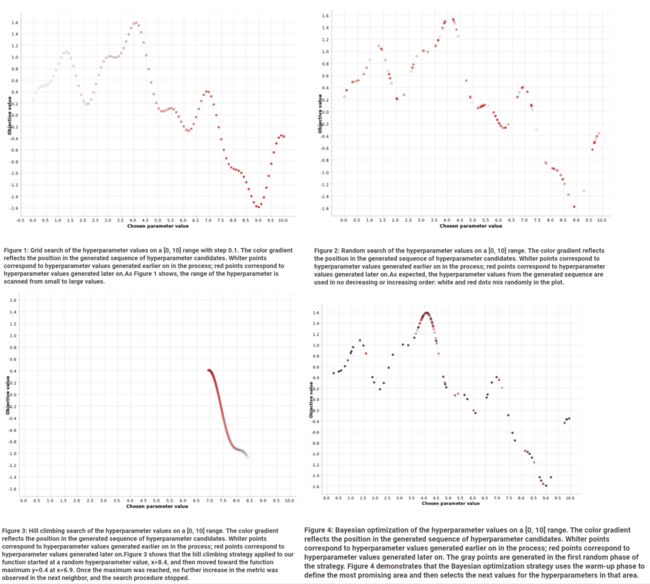
上述方法各有区别，各有特点，搜索空间大的耗时耗算力，但准确，因此都是一个tradeoff问题，同时目前有很多超参数调试工具（AutoML技术、 Optuna工具等）可以解决问题。

1.2 强化学习超参数选择与调优

这一块的工作目相对不太多，其中A3C算法中提到了针对learning rate的网格搜索。

另外一个比较扎实的工作就是由Peter Henderson发表的Deep Reinforcement Learning that Matters, 详细分析了不同超参数对算法效率的影响，但具体的也没谈多少关于超参的选择。

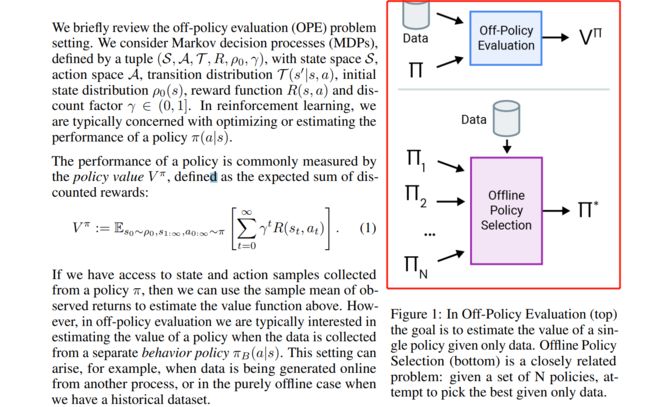
1.3 OPE(off-policy & Offline Evaluation)方法

在离线强化学习中，函数优化的目标被定义为最小化 $MSE(V)$ 过程，表示为：

其中会涉及两个非常重要的概念：off-policy Evaluation 和offline policy evaluation, 区别如图：

图中很明确的指出了off-policy E和offline policy E的区别，off-policy是从一个policy中找到最有的 ${\pi }^{\ast }$ , 而offline中则是从 $n$ 中找到一个最优的 ${\pi }^{\ast }$

此外， off-policy evaluation通常包括Inverse Propensity Scoring (IPS) Methods、Doubly-Robust Methods (DRM)、Direct Methods (DM)三种方法，如图所示：

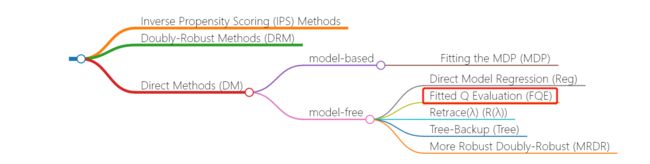
2. Offline Rl 超参数选择方法

在解释具体的算法之前，首先阐述一下两个概念：

• hyperparameter tuning/optimization： 超参数调优，也称为超参数优化，是寻找能够产生最佳性能的超参数配置的过程。
• hyperparameter selection： 选择不同的参数去调优模型。

2.1 超参数选择原理

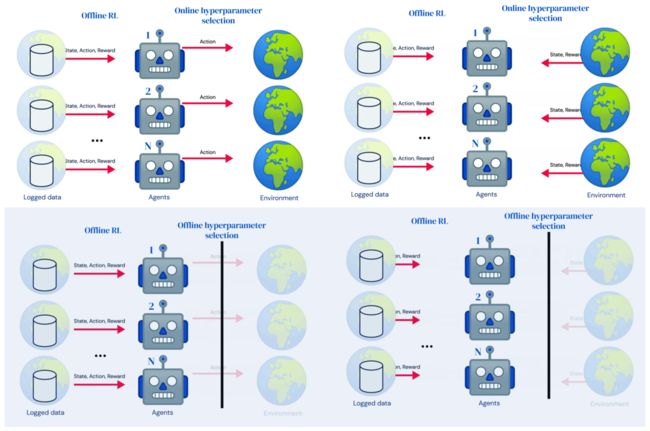
我们从图中可以看到online和offline hyperparameter的区别，offline不像online那样可以直接在智能体中调整超参数，而是多了一条黑线，问题可以简化为下面的如何从策略空间中找到一个最有策略，使得 ${\int }_{s\in S_0}\widehat{V^{\pi }}(s,\mathcal{D})ds$ 最大化。

本质就是不断地去policy optimization使得policy evaluation最佳。

2.2 Offline Statistics for Policy Ranking

2.2.1 OHS流程

1. 使用几种不同的超参数设置训练离线 RL 策略。
2. 对于每个策略，计算总结策略性能的标量统计信息（无需交互与环境）。
3. 根据summary statistics选择top k最佳策略在真实环境中执行。

作者通过计算基于评论家 $Q_{\theta }$ 和数据集 $D$ 的统计量来计算标量值，以便对策略进行排序，主要通过以下两种方式：

2.2.2 OPE质量

2.3 评估OHS的指标

• Spearman’s rank correlation, 首先根据汇总统计和实际值计算不同策略的排名值。 Spearman 秩相关是两组秩值之间的 Pearson 相关

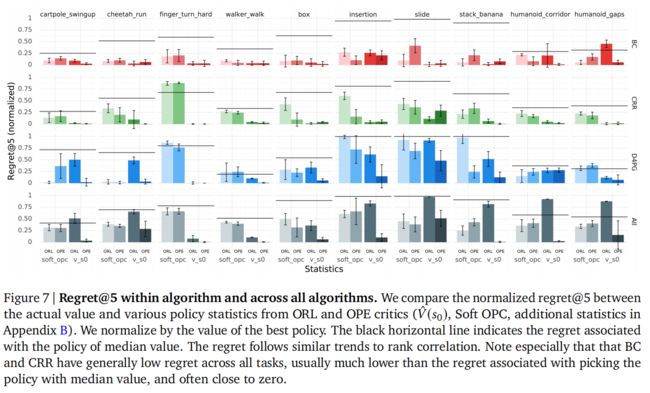
• Regret@k，首先计算前 k 个集合，即具有最高汇总统计值的 k 个策略。 Regret@k是整个集合中最佳策略的实际值与top-k集合中最佳策略的实际值之差。 该指标旨在回答以下问题：“如果我们能够在实际环境中运行与 k 个超参数设置相对应的策略，并通过这种方式获得对其值的可靠估计，那么我们选择的集合中的最优值与所有最优值之间的差距有多大？ 是否考虑了超参数设置？”。
• Absolute error，统计量 $\hat{V}(S_0)$ 与实际值之差的绝对值。 这并不直接衡量排名质量，但我们将其包括在此处，因为零绝对误差对应于完美排名，并且因为它是 OPE 文献中的标准衡量标准。

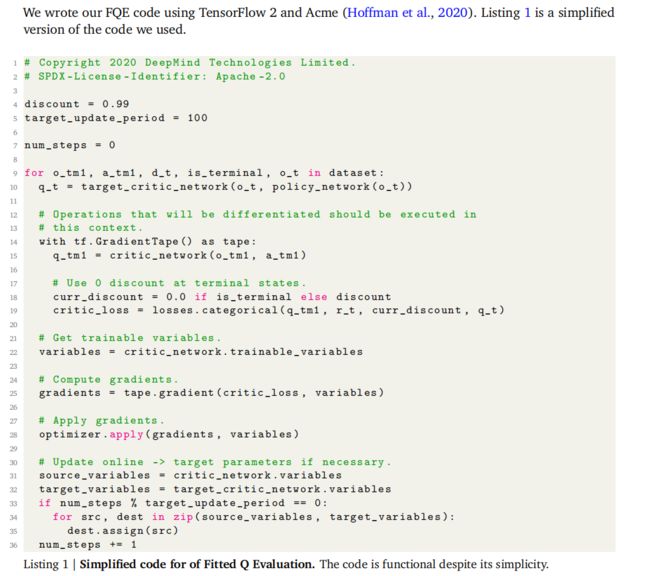
2.4 FQE(Fitted Q Evaluation)算法

2.4.1 原理

2.4.2 实验环境

本文作者在DM Control Suite、Manipulation tasks和DM Locomotion环境上进行实验。

2.4.3 实验对比算法

2.4.4 代码实践

3. 实验及结果分析

3.1 过估计(Overestimation)

作者发现一个明显的高估趋势——statistics对D4PG的估计最多，其次是CRR，其次是BC。且BC和CRR试图产生类似于行为策略的策略，而D4PG则没有。这可能会更容易估计它们生成的策略的价值。在任务领域方面，statistics往往对DM运动的估计最多，其次是Manipulation，其次是DM控制套件。

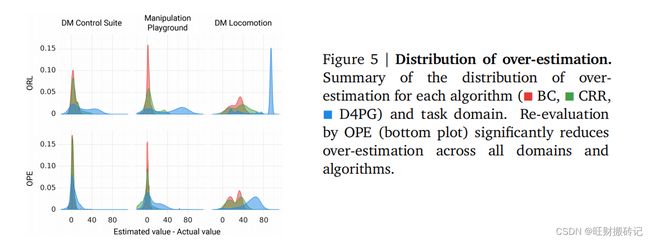
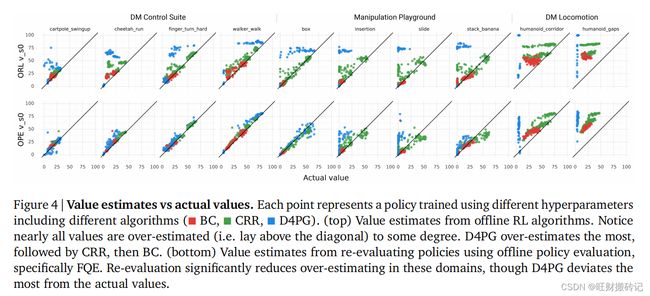
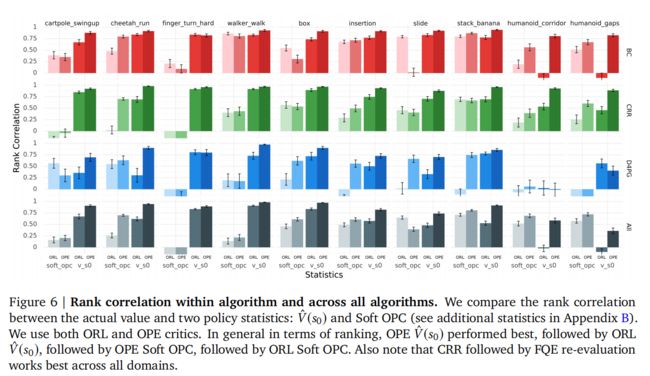
3.2 排名质量(Ranking Quality)

3.3 FQE 对其自身超参数的敏感性( FQE Sensitivity to Its Own Hyperparameters)

参考文献

[1]. Tom Le Paine, Cosmin Paduraru, Andrea Michi, Caglar Gulcehre, Konrad Zolna, Alexander Novikov, Ziyu Wang, Nando de Freitas: “Hyperparameter Selection for Offline Reinforcement Learning”, 2020; arXiv:2007.09055.
[2]. Siyuan Zhang, Nan Jiang: “Towards Hyperparameter-free Policy Selection for Offline Reinforcement Learning”, 2021; arXiv:2110.14000.
[3]. https://www.youtube.com/watch?v=2mvGE2KxQXA
[4]. https://slideslive.com/38967635/towards-hyperparameterfree-policy-selection-for-offline-rl?ref=speaker-17826
[5]. https://www.knime.com/blog/machine-learning-algorithms-and-the-art-of-hyperparameter-selection
[6]. Justin Fu, Mohammad Norouzi, Ofir Nachum, George Tucker, Ziyu Wang, Alexander Novikov, Mengjiao Yang, Michael R. Zhang, Yutian Chen, Aviral Kumar, Cosmin Paduraru, Sergey Levine, Tom Le Paine: “Benchmarks for Deep Off-Policy Evaluation”, 2021; arXiv:2103.16596.
[7]. Cameron Voloshin, Hoang M. Le, Nan Jiang, Yisong Yue: “Empirical Study of Off-Policy Policy Evaluation for Reinforcement Learning”, 2019; arXiv:1911.06854.
[8]. Hoang M. Le, Cameron Voloshin, Yisong Yue: “Batch Policy Learning under Constraints”, 2019; arXiv:1903.08738.

---

OfflineRL推荐阅读

离线强化学习(Offline RL)系列4：(数据集) 经验样本复杂度(Sample Complexity)对模型收敛的影响分析
离线强化学习(Offline RL)系列4：(数据集)Offline数据集特征及对离线强化学习算法的影响
离线强化学习(Offline RL)系列3: (算法篇) AWAC算法详解与实现
离线强化学习(Offline RL)系列3: (算法篇) AWR(Advantage-Weighted Regression)算法详解与实现
离线强化学习(Offline RL)系列3: (算法篇) Onestep 算法详解与实现
离线强化学习(Offline RL)系列3: (算法篇) IQL(Implicit Q-learning)算法详解与实现
离线强化学习(Offline RL)系列3: (算法篇) CQL 算法详解与实现
离线强化学习(Offline RL)系列3: (算法篇) TD3+BC 算法详解与实现（经验篇）
离线强化学习(Offline RL)系列3: (算法篇) REM(Random Ensemble Mixture)算法详解与实现
离线强化学习(Offline RL)系列3: (算法篇)策略约束 - BRAC算法原理详解与实现(经验篇)
离线强化学习(Offline RL)系列3: (算法篇)策略约束 - BEAR算法原理详解与实现
离线强化学习(Offline RL)系列3: (算法篇)策略约束 - BCQ算法详解与实现
离线强化学习(Offline RL)系列2: (环境篇)D4RL数据集简介、安装及错误解决
离线强化学习(Offline RL)系列1：离线强化学习原理入门