贝叶斯推理——概率思维
作者:财小米
链接:https://www.jianshu.com/p/954b34a33578
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
人生中最重要的问题,在绝大多数情况下,真的就只是概率问题。 ——皮埃尔-西蒙·拉普拉斯(1749-1827)
几道测试题
1.王二是一个普通大学毕业的本科生。那么请问他更可能是下面哪种职业?
A:张江程序员
B:陆家嘴金融男
2.有一天王二去相亲遇到了张小花,张小花长的像下面这个妹子。请问张小花的职业更可能是下面哪种?
A:模特
B: 职员
C: 胸器逼人的职员
3.和张小花相亲之后,王二被迷得神魂颠倒,但小花对王二却忽冷忽热。情人节到了,小花给王二送了盒巧克力,请问小花喜欢王二的概率有多大?
4.时光荏苒,王二被小花甩了之后,王二喜欢鬼混,有一天忽觉身体不适,怀疑自己是不是得了花柳病。王二查资料发现,HIV在健康男性中总体发病率为0.1%。王二不放心,去医院检查,结果呈HIV阳性。医生告诉他,咱医院的设备还是很先进的,准确率高达95%;请问王二得艾滋病的概率是多少?
人人都需要一点概率知识
有人还需要一点贝叶斯概率知识,比如王二。
首先说说什么是概率?
概率不是一个简单的概念。逻辑学家和统计学家互相争论,提出了多个关于概率的定义,全都非常精确。然而对我们外行人来说,概率(在日常生活中和“可能性”是同义词)是一个相对含糊的概念,与不确定性,倾向性,貌似正确及出乎意料等词紧密相关。
其实,概率有两种。
1是客观概率
我们初中,高中学的概率,是一个客观的概念。比如,掷骰子出现点数1的概率是六分之一。可以解释为,丢很多次骰子,平均有六分之一的次数会出现点数1,可以用频率去解释。每人计算出的概率也都是相同的。又比如,问题4中,王二患艾滋病的概率。
2是主观概率
还有一种概率,没法用客观概率去解释,比如问题3中,张小花喜欢王二的概率。王小花是独一无二的,没法用多个王小花喜欢王二的频率去解释。但可以这么解释:你内心描绘的类似“信念程度”这样的概念。是一种主观概率。
什么是贝叶斯推理?
什么是贝叶斯推理?
一句话概括就是,我们根据新的信息/证据/数据来更新看法/判断/信念。
试问谁人不是如此,人人都在用,但多数人都是用而不自知。
我们天生就是贝叶斯动物。
托马斯·贝叶斯(Thomas Bayes)是18世纪初苏格兰的一位神父。他想证明上帝存在,用了两个步骤:第一步,如果上帝存在,就会有如此这般的事情发生;第二步反过来,如果如此这般的事情发生,那么我们对上帝存在的信心会增加多少?
贝叶斯推理本质上是条件概率的变形,已知如果a则b,反过来求解如果b则a的概率。是不是有点晕了,别担心,听我给你一一分解。
我们再看一遍贝叶斯推理的概括:我们根据新的信息/证据/数据来更新看法/判断/信念。
这句话可以分成三部分:
旧的看法/判断/信念
新的信息/证据/数据
新的看法/判断/信念
这三部分可用数学语言概括如下
先验概率(旧的看法/判断/信念)
条件概率(新的信息/证据/数据)
后验概率(新的看法/判断/信念)
完整的贝叶斯推理可以概括为如下几个步骤
通过经验或者历史数据设定“先验概率”
设置发生某事件的“新信息“
通过观察到的行为排除掉不可能的情况
将先验概率更新为“后验概率”
先验概率
先验概率,是获得新信息之前,各个类别存在的概率。
回看问题1,你认为王二是程序员还是金融男?
你猜程序员是吧?
为啥啊?
程序员的基数比金融男大多了啊。
现实是,10个里面,8个程序员2个金融男。
这就是先验概率,在我进一步了解王二之前,只能毛估着来。
这个基于经验或者历史数据推断出发毛估估的概率就是先验概率。
程序员的先验概率是:8/10=0.8
金融男的先验概率是:2/10=0.2
条件概率
条件概率是指,事件a在事件b已经发生条件下的发生概率。
P(A) —事件a发生的概率
P(B)—事件b发生的概率
P(A|B) —在事件b发生的条件下事件a发生的概率
我们回看一下问题3,
“小花给王二送了巧克力”这个是新的已经发生的信息,即事件b
”小花喜欢王二”就是事件a
我们要求解的问题就是,
P(A|B)=P(小花喜欢王二 | 小花给王二送了巧克力 )
读做,在小花给王二送了巧克力这一条件下,小花喜欢王二的概率。
先不急着求解,我们继续。
后验概率
通过新信息将先验概率通过贝叶斯更新,就可以转换为“后验概率”
啥意思呢?
举个例子
我们常说“吃一堑长一智”,
旧智,就相当于先验概率;
新智,就相当于后验概率;
吃的那一堑,就是新信息。
从“旧智”到“新智”就是贝叶斯更新。
再举个例子,回到上面的问题4
王二患艾滋病的概率是多少?
95%?
No!
贝叶斯定理的计算
现在我们用问题4,来完整演算一遍贝叶斯概率的计算过程。
贝叶斯定理公式

当然我们不需用公式去计算,太麻烦,记不住,记住也会忘。
前几天学到了一个热别牛叉的方法,叫图解法,是人就能学会,不会不是中国人。
我们回顾一下题目:
4.时光荏苒,王二被小花甩了之后,王二喜欢鬼混,有一天忽觉身体不适,怀疑自己是不是得了花柳病。王二查资料发现,HIV在健康男性中总体发病率为0.1%。王二不放心,去医院检查,结果呈HIV阳性。医生告诉他,咱医院的设备还是很先进的,准确率高达95%;请问王二得艾滋病的概率是多少?
1.先找“先验概率”
“HIV在健康男性中总体发病率为0.1%”换句话说,在1000个人中有1个HIV患者,999个健康人
图示如下:
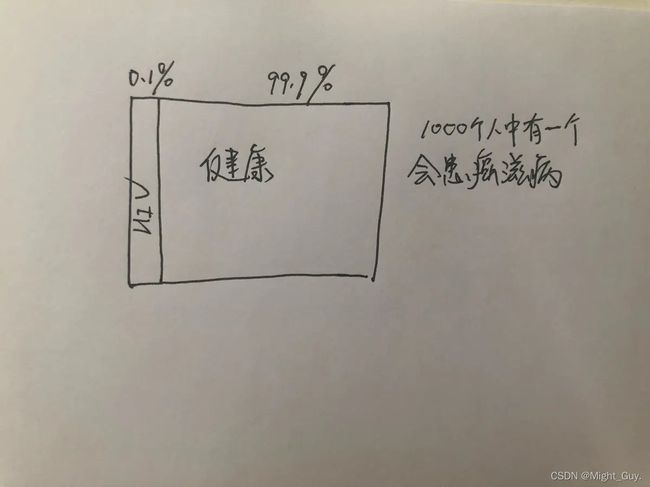
该图表示的是:在接受检查之前,判断是否患艾滋病的可能性。王二所在的世界分成左侧表示“罹患艾滋病”和右侧“身体健康”的两个“可能世界”,二王二一定处在两个当中的一个。但并不知道是在哪一个,仅仅是推测而已。通过流行病学数据王二知道,1000个人中就有1个有艾滋病。所以,王二在没有去医院检查前,推算属于左侧的概率是0.1%,属于右侧是99.9%
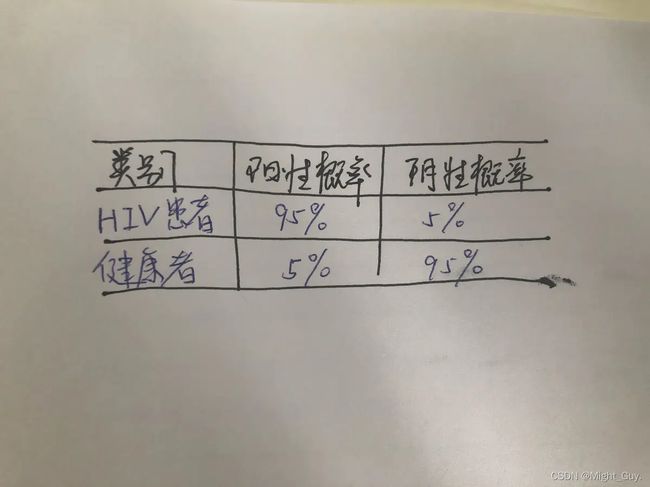
2.以检查准确率为线索,设定“条件概率”
本例中,新信息指“王二的检查结果呈阳性”和“检查的准确率”
先看第二个新信息,从医生的话中,我们可以得出如下信息:
一是上面一行,本来是患者结果有5%没检查出来,属于漏检;
二是下面那行,本来是健康人,结果有5%检查为患者,属于误检;
所以医院检查的结果可以分为以下这么几类:
1.健康检出阳性
2.健康检出阴性
3.患者检出阳性
4.患者检出阴性
如下图所示:
也就是说,因为王二已经观察到了“阳性”这一结果,所有的“阴性”结果便可排除掉了。阴性结果有些啥呢?两种。
一是,“患者检查出阴性”
二是,“健康检查出阴性”
排出这两种之后,用图形表示如下:
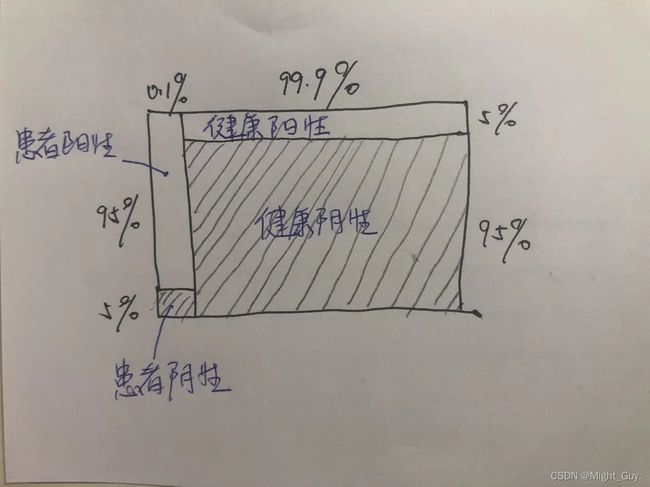
3.计算后验概率
由于“阳性”这一诊断结果,可能世界被限定为2个,也就是王二所处的世界要么是“患者检查出阳性”,要么是“健康检查出阳性”,两种可能性。对检查结果的观察,使得可能性从4种变成2种。这样概率相加之和(上图中长方形的面积)无法为1 。因此,为了恢复标准化条件(概率相加之和为1),需在保持比例关系的条件下,使之“相加之和等于1”。
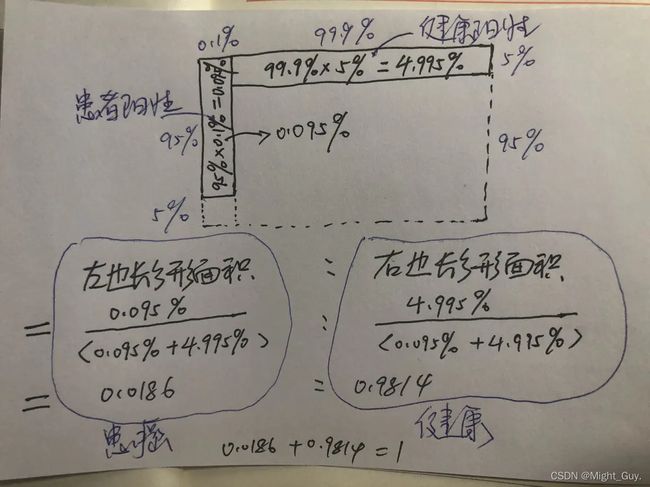
从上图结果可以得知,在得知“阳性”这一检查结果的情况下,王二患艾滋病的概率为1.86%,不到2%,这便是后验概率。
从后验概率看,王二的天并没有塌下来,他可以继续鬼混了。哈哈
我们再此总结下,贝叶斯推理的顺序:
1.先验概率
2.条件概率
3.获新信息
4.后验概率
在解决王二问题时,我们是知道先验概率的,是有客观数据做参考的。
那么,像问题3这种,信息比较少的情况下能否做贝叶斯推理呢?
答案是,可以的。
这也正是贝叶斯推理的牛逼之处。
怎么做呢?
我们利用问题3,再巩固一下这一推理流程。
信息不足下的贝叶斯推理
3.和张小花相亲之后,王二被迷得神魂颠倒,但小花对王二却忽冷忽热。情人节到了,小花给王二送了盒巧克力,请问小花喜欢王二的概率有多大?
1.找“先验概率”
张小花是否喜欢王二呢?没有大数据可查,他两相亲第一次见面。这种情况下,一般可以采用“理由不充分”原理,暂且把“喜欢”,“ 不喜欢”这两种情况的概率视为相等。也就是先验概率分别为0.5,0.5
2.找条件概率
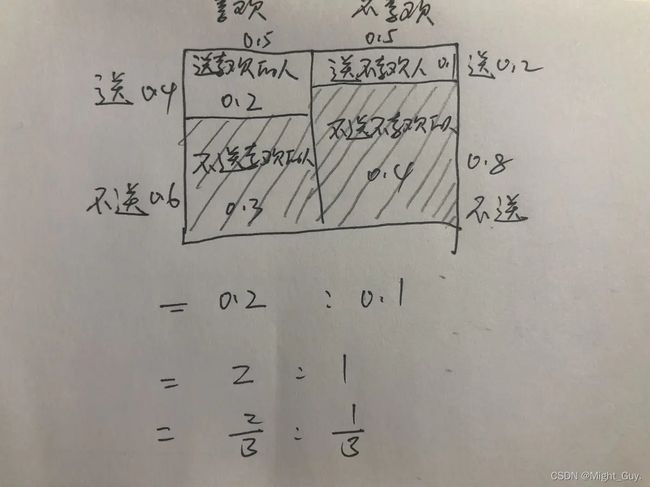
王二在某调查网站发现,情人节,女生给喜欢的人送出巧克力的概率是0.4;女生给普通朋友送出巧克力的概率是0.2;
3.寻找新信息
王二在情人节,收到了小花的巧克力。
4.得出后验概率
在收到巧克力前,张小花喜欢王二的概率为50%,通过送巧克力这一行为之后,概率上升到了66%,这也符合我们的生活经验。贝叶斯推理的便利之处在于,能够将其通过数值表达出来。
贝叶斯推理饿便利之处还在于,数据很少的情况下也可以进行推测,数据越多,推测的结果越准。
贝叶斯推理的牛叉之处还在于,对获得的信息可以做出瞬时反应,自动升级推测,将先验概率更新为后验概率,具备了学习功能。
我们也是这学习的,从这个角度讲,贝叶斯推理人人都该会,人人都该用;人人都该会而常用,用而自知。
贝叶斯推理的本质
贝叶斯推理的本质是什么?
求解某事的条件概率。
问题3,求解的是,在小花给王二送了巧克力这一条件下,小花喜欢王二的概率。
P(A|B)=P(小花喜欢王二 | 小花给王二送了巧克力 )
问题4,求解的是,在王二检查出HIV阳性的这一条件下,王二患艾滋病的概率。
P(A|B)=P(王二患艾滋病| 王二检查出HIV阳性)
有兴趣的你,可以计算下下面几道题的条件概率
1.某小孩生在上海,那么他上私立小学的概率;
2.某小孩上了私立小学,那么他上著名私立初高中的概率
3.某小孩上了著名私立初高中,那么他考上清北的概率
4.某小孩上了清北,那么他成为人生赢家的概率。
《从0到1》的作者彼得•蒂尔说:如今的哈佛等名校录取,已经成为一场超级智力测试。
比尔•盖茨小时候也上各种补习班的。
扎克伯格就读的高中,菲利普斯埃克塞特学院是美国最顶尖的私立寄宿高中之一,被《经济学人》列为"英美私立高中第一梯队"。
该校 SAT 平均成绩在 300 多所美国私立寄宿高中里经常排名第一,每年近三分之一毕业生被常春藤联盟等名校录取。
清北有更优的牛逼条件概率
著名私立高中有更优的清北条件概率
生于大城市有更优的私立初高中条件概率。
练习题
一辆出租车在夜晚肇事后逃逸。 这座城市有两家出租车公司,其中一家公司的出租车是绿色的,另一家是蓝色的。 你知道以下数据:
这座城市85%的出租车是绿色的,15%是蓝色的。
一位目击证人辨认出那辆肇事出租车是蓝色的。当晚,警察在出事地点对证人的证词进行了测试,得出的结论是:目击者在当时能够正确辨认出这两种颜色的概率是80%,错误的概率是20%。
肇事出租车是蓝色的概率是多少?
ps:哦,好像问题2没用到。whatever,放着吧,下次继续。