分享本周所学——布尔代数与谓词逻辑入门
大家好,欢迎来到《分享本周所学》第五期。本人是一名人工智能初学者,因为马上要上大学了嘛,就想着提前稍微预习一下大一课程,然后最近一周学了一下基础的布尔代数和谓词逻辑,觉得好像挺有意思还有点用,就想把学到的东西分享给大家。
这篇文章会尽量用比较通俗的语言解释所有的概念,所以可能不会特别注重严谨性,希望大家理解。
看这篇文章之前,我默认你学过基础的编程,知道bool型(在有的语言中叫boolean,反正就是那个要么true要么false的变量类型)变量的基本使用方法,能够使用if条件句。
这篇文章主要参考了曼彻斯特大学一年级课程Mathematical Techniques for Computer Science的教材。教材是公开的,链接如下:
9月4日更新:教Mathematical Techniques for Computer Science的教授似乎已经已经不讲布尔代数这部分了,于是他在教材里把这章删掉了……麻烦大家去我的Gitee仓库下载老教材:
9月20日更新:很抱歉,教材现在似乎只对在读学生公开了,根据学校的教学内容版权要求,我不得不移除文章内的所有教材链接,请大家谅解。
目录
一、啥是布尔代数
1. 基础布尔运算
2. 布尔运算律
3. 合取范式与析取范式
4. 简化布尔表达式
5. 布尔代数的推广
二、谓词逻辑
1. 任意与存在
2. 在布尔代数中使用任意与存在
3. 任意和存在的德·摩根定律
三、凭啥要我学布尔代数
四、答案
1. 第一题
2. 第二题
3. 第三题
上期文章链接:《分享本周所学——使用Flask实现Python程序服务化》![]() https://blog.csdn.net/weixin_48978134/article/details/125770821?spm=1001.2014.3001.5501
https://blog.csdn.net/weixin_48978134/article/details/125770821?spm=1001.2014.3001.5501
本期封面:
一、啥是布尔代数
“布尔代数”。听到这个名字我相信CSDN里很多程序员朋友们是这样想的:布尔,就是bool嘛,要么是true要么是false的那个变量,所以布尔代数是不是就是算if后面那个条件句是true还是false?这有学的必要吗?
应该说,这种想法对了但没完全对,因为布尔代数涵盖的不只是算个逻辑条件句那么简单。
1. 基础布尔运算
其实狭义上的布尔运算就是对bool型变量进行运算。基本的布尔运算总共有3种,AND(合取,即与运算)、OR(析取,即或运算)和NOT(否定,即非运算)。这个相信大家都不陌生,所以我在这就简单地提一句。我们假设A和B都是bool型变量。
A AND B表示如果A和B同时为true,结果为true,否则结果为false。这个运算在Python里叫and,在姓C的语言和一些其他语言里是&&。在布尔代数中,我们用![]() 表示,也就是
表示,也就是![]() 。
。
A OR B表示如果A和B中有一个为true,结果为true,否则结果为false。这个运算在Python里叫or,在姓C的语言和一些其他语言里是||。在布尔代数中,我们用![]() 表示,也就是
表示,也就是![]() 。
。
NOT A表示如果A为false,结果为true,否则结果为false。这个运算在Python里叫not,在姓C的语言和一些其他语言里是!。在布尔代数中,我们用![]() 表示,也就是
表示,也就是![]() 。
。
这里注意一下,NOT的运算要优先于AND和OR,就像乘法的运算要优先于加法一样。所以,如果我们要计算![]() ,要先对A和B计算NOT,然后再计算AND。在编程中也是一样,以下代码分别演示Python和C++中AND的NOT的计算顺序,两种语言中都是优先计算NOT。
,要先对A和B计算NOT,然后再计算AND。在编程中也是一样,以下代码分别演示Python和C++中AND的NOT的计算顺序,两种语言中都是优先计算NOT。
a = True
b = False
print(not a and b)
# Result: False#include
using namespace std;
int main() {
bool a = true, b = false;
cout << !a && b;
// Result: 0
} 为了确保大家对这几个运算符都足够熟悉,我这放一道简单的题大家算一下啊。当A=false,B=true时,计算以下布尔表达式的值:
![]()
答案我会放在文章末尾,算完的朋友们可以去翻到末尾对一下答案。
2. 布尔运算律
布尔运算律其实就是算布尔表达式的时候用到的一些技巧。我就直接把所有基本的运算律全都放在下面了。这些运算律并不复杂,基本上看一眼就能明白什么意思,有的甚至简单到看起来像废话一样,所以我这里就不作解释和证明了。这里提一句,![]() 这个符号叫做语义等价,表示左右两端的布尔表达式等价。已知A、B、C为bool型变量:
这个符号叫做语义等价,表示左右两端的布尔表达式等价。已知A、B、C为bool型变量:
- 双重否定:
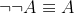
- AND运算德·摩根定律:
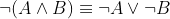
- OR运算德·摩根定律:

- 幂等性:
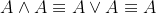
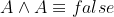
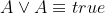
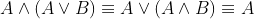
- AND运算分配律:

- OR运算分配律:
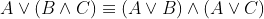
3. 合取范式与析取范式
我们来看一下以下的布尔表达式:
![]()
显然啊,这个表达式看起来比较凌乱,没有什么规律可言。为了更好的了解一个布尔表达式的性质,我们通常需要对它进行整理和简化。我们一般希望把一个布尔表达式整理成这样的形式:
![]()
这个形式叫做合取范式。如果你没看懂上面的式子,大概解释一下就是一大堆小表达式用AND连起来,每个小表达式都是一堆bool变量用OR连起来。
那怎么才能把上面那个乱七八糟的式子变成一个整洁的合取范式呢?其实很简单啊,就分两步。第一步就是找到所有![]() 和
和![]() 形式的式子,然后用德·摩根定律把括号拆掉。比如我们现在想要简化上面的那个式子,第一步应该这么干(由于CSDN自带的LaTeX编辑器不是很好用,我就在别的地方编辑好之后以图片的形式粘过来):
形式的式子,然后用德·摩根定律把括号拆掉。比如我们现在想要简化上面的那个式子,第一步应该这么干(由于CSDN自带的LaTeX编辑器不是很好用,我就在别的地方编辑好之后以图片的形式粘过来):
注意一下,第一步干完之后如果某个变量前面有双重否定,记得把双重否定去掉。第二步要用AND运算分配律把所有含有AND的括号拆掉,大概是这个样子:
然后你会发现我们就得到了一个完美的合取范式。
其实还有一种整理布尔表达式的方式,叫做析取范式。析取范式是这样一个形式:
![]()
说白了就是合取范式反过来。把布尔表达式转换成析取范式也是两步,第一步和合取范式一样,第二步改成用OR运算分配律去拆掉所有含有OR的括号。如果把上面的式子转化成析取范式,步骤是这样的:
这就比较尴尬了。为什么尴尬呢?因为你会发现我们把第一步做完的时候,这个式子就已经变成一个析取范式了。所以对于这个式子来说,转化成析取范式要比转化成合取范式简单很多。但是并不是所有布尔表达式都是这样,也有的式子转化成合取范式会更简单一些。
4. 简化布尔表达式
把一个式子转化成合取或者析取范式还不算完,因为我们还可以对我们得到的式子进一步的简化。我们就拿刚才的合取范式举例子吧。为了方便阅读,这里重新放一下刚刚算出来的合取范式:
![]()
首先看第一个括号啊,有一个![]() ,这个显然等于true。所以第一个括号就等于true。所以第一个括号没啥用,可以直接删掉。然后是第二个括号,有一个
,这个显然等于true。所以第一个括号就等于true。所以第一个括号没啥用,可以直接删掉。然后是第二个括号,有一个![]() ,根据幂等性这个显然等于
,根据幂等性这个显然等于![]() ,所以第二个括号其实就是
,所以第二个括号其实就是![]() 。第三个括号似乎不能简化,第四个括号也是根据幂等性可以简化成
。第三个括号似乎不能简化,第四个括号也是根据幂等性可以简化成![]() 。所以上面这个式子其实可以简化成:
。所以上面这个式子其实可以简化成:
![]()
但是还没完啊,我们看到第二和第三个括号里都有![]() ,所以根据运算律第7条,这个算式可以进一步简化成:
,所以根据运算律第7条,这个算式可以进一步简化成:
![]()
到这里就算简化完了,大家可以看到我们最后得到的这个式子非常的简单而且直观。大家可以试试自己把上面那个析取范式简化一下啊,答案我会放在文章末尾。
5. 布尔代数的推广
省流:与本文其他内容无关,也不是特别重要,不想看就算了。
其实啊,布尔代数并不仅仅是局限于bool型变量的运算。布尔代数里的这些运算是可以推广到其他地方的。但是如果参与运算的变量不再是bool型变量,那我们目前对![]() 、
、![]() 和
和![]() 的定义似乎也不太合适了。我们需要重新定义一下这些运算。那具体怎么定义呢?这其实取决于布尔集。那什么是布尔集呢?其实就是我们参与运算的变量的取值的集合,一般用
的定义似乎也不太合适了。我们需要重新定义一下这些运算。那具体怎么定义呢?这其实取决于布尔集。那什么是布尔集呢?其实就是我们参与运算的变量的取值的集合,一般用![]() 表示。比如说,我们之前仅仅是对bool型变量进行运算,bool型变量的取值的集合是{true, false},所以此时
表示。比如说,我们之前仅仅是对bool型变量进行运算,bool型变量的取值的集合是{true, false},所以此时![]() 。
。
那还有什么常见的布尔集呢?一个很常见的例子是将一个集合的幂集作为布尔集。那什么是幂集呢?幂集其实就是一个集合的所有子集的集合,比如说{true, false}的子集有四个:{true, false}、{true}、{false}、![]() 。所以,{true, false}的幂集就是{{true, false}, {true}, {false},
。所以,{true, false}的幂集就是{{true, false}, {true}, {false}, ![]() },我们用S表示这个幂集。那我们怎么在S上定义布尔运算呢?其实很简单,我们将
},我们用S表示这个幂集。那我们怎么在S上定义布尔运算呢?其实很简单,我们将![]() 定义为交集
定义为交集![]() ,将
,将![]() 定义为并集
定义为并集![]() ,将
,将![]() 定义为补集
定义为补集![]() 。比如,假设变量A为{true},变量B为{false},那
。比如,假设变量A为{true},变量B为{false},那![]() 就是
就是![]() ,也就是
,也就是![]() ,而
,而![]() 就是{true, false},
就是{true, false},![]() 就是{false}。
就是{false}。
其实定义布尔集和布尔运算的方法还有很多,但是无论怎么定义,这些运算必须满足以下条件。设![]() :
:
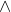 和
和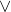 满足交换律和结合律;
满足交换律和结合律;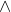 和
和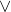 满足分配律,即
满足分配律,即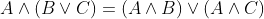 ,
,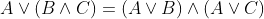 ;
;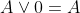 ,其中
,其中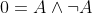 ;
;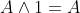 ,其中
,其中 。
。
不过在这篇文章中,我们默认布尔集![]() 。
。
二、谓词逻辑
谓词逻辑听上去像是在讲英语语法之类的东西,但是其实不是,谓词逻辑也是数学中一个很重要的领域。不过因为这次我们是入门,所以只会聊到谓词逻辑中的两个概念,这两个概念大家肯定也都听说过。
1. 任意与存在
任意与存在这两个东西应该是大家上高中就学了的,不过以防大家忘了我还是提一句。
任意,顾名思义,就是随便选一个都能符合条件。我们平时日常生活中经常会用到“任意”这个概念,比如说,“炉石传说任意选一个职业,我都会玩”。任意用符号![]() 表示,那么上面那句话如果用数学语言就可以写成:
表示,那么上面那句话如果用数学语言就可以写成:
![]()
为了避免有朋友没玩过炉石,我解释一下,大括号里的是炉石传说的十个职业。
而存在则表示有一个符合条件的就行,当然也可以有不止一个符合条件的,比如“炉石传说存在我会玩的职业”。存在用![]() 表示,那上面这句话就可以写成:
表示,那上面这句话就可以写成:
![]()
当然,任意和存在还是更多被应用在数学场景,比如“对于任意实数a,存在实数b,使得a与b的和为0”这句话,可以用以下语句表示:
![]()
2. 在布尔代数中使用任意与存在
任意和存在这两个概念是可以作为运算符被融进布尔代数里的。
我们先来看任意。一般一个含有任意的布尔表达式会写成![]() 这样的形式,其中A是一个关于x的布尔表达式。计算这个表达式的结果也很简单,我们只需要找到把x的定义域内的所有值都试一遍,如果x取所有这些值的情况下A(x)都等于true,那么我们就可以说
这样的形式,其中A是一个关于x的布尔表达式。计算这个表达式的结果也很简单,我们只需要找到把x的定义域内的所有值都试一遍,如果x取所有这些值的情况下A(x)都等于true,那么我们就可以说![]() ,否则
,否则![]() 。
。
存在则相反。如果x的定义域内只要有一个值使A(x)为true,那么![]() ,只有在x取所有这些值的情况下A(x)都为false,才可以说
,只有在x取所有这些值的情况下A(x)都为false,才可以说![]() 。
。
值得注意的是,任意和存在的运算优先级在NOT之后、在AND和OR之前。也就是说,如果一个布尔表达式里面同时出现了AND、OR、NOT、任意和存在,在没有括号的情况下,我们要先计算NOT,然后计算任意和存在,最后计算AND和OR。
说到这里,我觉得我们是时候规范一下布尔表达式的定义了。只有满足下列条件的式子,我们才能称之为布尔表达式:
- 如果x是一个布尔变量,那么
 和
和 是布尔表达式;
是布尔表达式; - 如果x、y是布尔表达式,那么
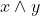 和
和 是布尔表达式;
是布尔表达式; - 如果A(x)是一个关于x的布尔表达式,那么
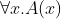 和
和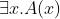 是布尔表达式。
是布尔表达式。
3. 任意和存在的德·摩根定律
我们可以将德·摩根定律扩展到任意与存在这两个运算上。其实理解起来非常简单啊,所以我就直接放公式了:
![]()
![]()
我们可以利用这两个公式来对含有任意和存在的布尔表达式进行化简。比如下面这个式子:
![]()
我们先用德·摩根定律尽量把括号都拆掉,最后去掉所有的双重否定。整个过程是这样的:
那么最后还是留一道题考考大家。简化这个式子:
![]()
三、凭啥要我学布尔代数
看到这里大家可能会想,我为什么要学布尔代数这个东西啊?我平时编程根本不可能用到很复杂的布尔表达式啊。但是我觉得学布尔代数有三点好处。
第一,即使我们现在在程序中用不到庞大的布尔表达式,不代表以后用不到。我觉得,在一些实际开发场景当中,我们可能会在很多地方需要程序去作出大量的判断来检测某个对象的状态,在这些情况下,如果能够运用布尔代数去简化一个表达式,会使得我们的程序更易于理解和维护。另外,如果以后图形化编程得以普及,那在图形化编程中每个布尔表达式可能都会看起来十分庞杂。如果能恰当地使用布尔代数,将会大幅度地提高程序的简洁性和运行效率。
第二,布尔代数在电子工程这一领域的运用十分广泛。电子工程中所有涉及到逻辑门的内容全部都要用布尔代数去解决。布尔代数会给你在这个领域的学习和科研带来非常大的帮助。
第三,布尔代数可以很好地锻炼我们的思维能力,让我们像计算机一样严谨地去思考一个计算问题,有助于我们之后理解和编写代码。
四、答案
以下是本文中留给大家的三个小问题的答案。
1. 第一题
当A=false,B=true时,计算![]() :
:
2. 第二题
化简析取范式![]() :
:
![]()
3. 第三题
化简布尔表达式![]() :
:






