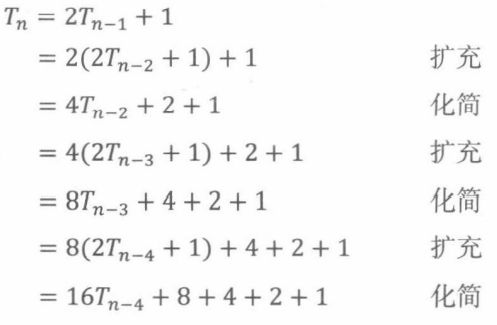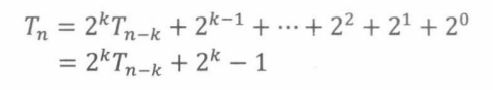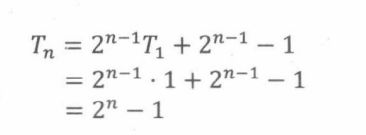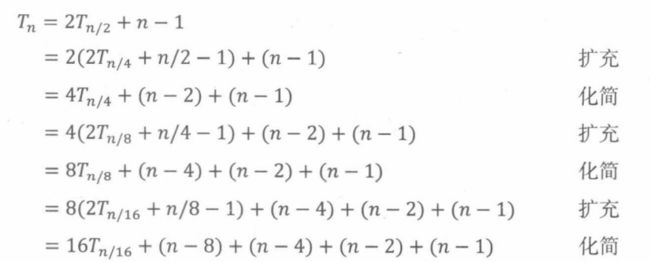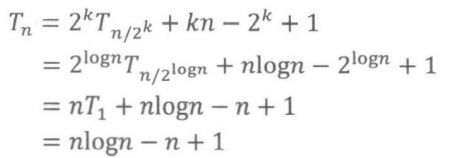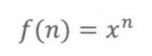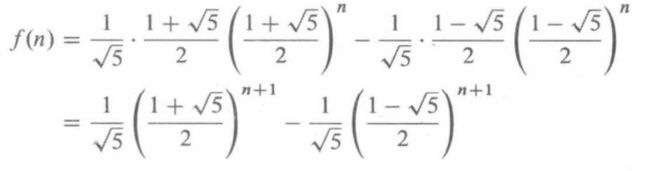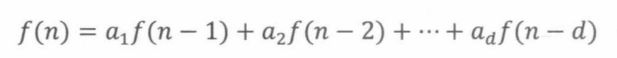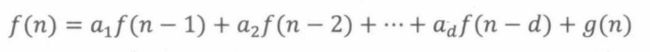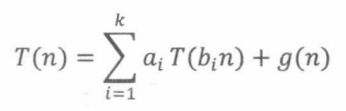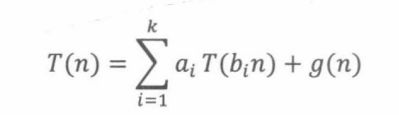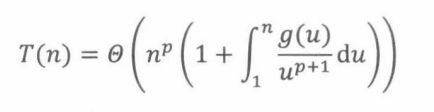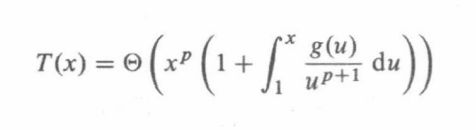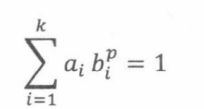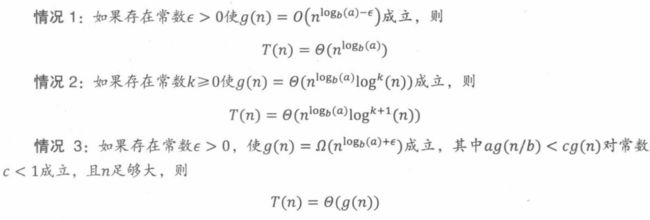第22章:递推
第22章:递推
22.1 汉诺塔
求解递推方程的方法有很多。最简单的办法是猜测一个方案,再用归纳证明法验证这个猜测是否正确。
例如,对于汉诺塔母函数的推导,观察前几个Tn值:1,3,7,15,31,63,一个很自然的猜测是 T n = 2 n 一 1 Tn= 2^n一1 Tn=2n一1。然后我们可以采用归纳法去证明我们的猜测。
由于递推公式和归纳证明法有着类似的结构,这样的验证证明过程特别简捷。具体来说,归纳证明的基础情形利用递推公式的第一行,即T;而归纳证明的归纳步骤利用递推公式的第二行,即前序项的函数Tn。
22.1.1上界陷阱
如果一个递推的解过于复杂,可以尝试证明某个简单的表达式是递推解的上界。例如汉诺塔问题的精确解是Tn= 2n - 1。我们可以尝试证明一个“更好”的上界Tn≤ 2 n 2^n 2n。
但是经过证明,这个证明不行啊!归纳证明经常出现这种情况,论证过程需要更强的假设才行。这并不意味着求递推解的上界行不通,而是这个例子中归纳和递归没有很好地融合在一起。
22.1.2扩充-化简法
猜测-验证法是求解递推等式的一种简单通用的方法。但是它有一个很大的缺点:你必须猜对。扩充-化简法就是另外一种求解递推的方法。扩充-化简法包含三个步骤,下面同样以汉诺塔问题为例进行解释说明。
步骤1:扩充和化简直到规律出现
第一步是用扩充(即应用递推,plug )和化简(即化简结果,chug)的方法扩展递推公式,直到规律出现。
经过几轮类似的扩充和化简,规律出现了。下列表达式似乎是成立的;
步骤2:验证规律
接下来我们要验证这个经过几轮扩充和化简得到的通式。
步骤3:用已知的前几项重写Tn
最后一步是将T,表示成已知的前几项的函数。令k = n-1,用T =1表示Tn,可得Tn的闭型表达式:
22.2 归并排序
首先介绍归并排序的工作原理。算法的输入是n个数字的列表,然后输出这些数字的非递减排序。有两种情况:
1、如果输入只有1个数字,算法什么也不做,因为列表已经是有序的了。
2、否则,输人列表包含两个或更多的数字。分别对列表的前一半和后一 半进行排序然后将两部分合并,得到一个n个数字的有序列表。
22.2.1寻找递推
排序算法的一个经典问题是:对n个项进行排序,最多需要比较多少次?为了保证每一步递归都能够平均切分输人,我们暂时假设n是2的幂。
1、如果输入列表只有1个数字,不需要比较,因此T1= 0。
2、否则, T n T_n Tn包括三部分:前一半列表排序的比较次数(最大为 T n / 2 T_{n/2} Tn/2 ),后一半列表排序的比较次数(同样最大为 T n / 2 T_{n/2} Tn/2 ),以及合并两部分列表的比较次数。合并阶段的比较次数至多为n -1。因为每次比较至少输出一个数字,当一个列表为空时输出余下的所有数字。最后n个数字都被输出,所以最多需要n -1次比较。
因此,归并排序n个项,所需的最大比较次数的递推公式如下:
22.2.2求解递推
步骤1:扩充和化简直到规律出现
规律出现了。看起来下述表达式似乎是成立的:
步骤2:验证规律
接下来,我们验证这个规律。
步骤3:用已知的前几项重写Tn
最后,我们用已知的前几项表示Tn。令k = logn,
22.3 线性递推
目前我们介绍了两种求解递推的方法:猜测-验证法和扩充-化简法。这两种方法都需要在数字或表达式的序列中发现规律。接下来,我们将给出两大类递推的程式化解法:不需要灵光乍现的灵感,只需要遵循步骤按图索骥。
22.3.1爬楼梯
爬n个台阶有多少种方法?我们可以一次爬一个台阶或两个台阶。
寻找递推
特例是,爬0个台阶有1种方法(什么也不做),爬1个台阶有1种方法(1小步)。一般地,爬n个台阶可以是爬n ―1个台阶然后迈1小步,或者爬n ―2个台阶然后迈1大步。因此定义递推:
这正是著名的斐波那契数的递推公式。
求解递推
一般地,齐次线性递推形如:
线性递推往往有指数解。所以,猜测
将这个猜测代入递推f(n) = f(n -1)+ f(n -2)得到:
解方程得到两个x的似真值
这说明,如果不考虑边界条件,递推至少有两个解。
定理22.3.1 如果f(n)和g(n)是齐次线性递推的两个解,那么对所有s,t ∈ R,h(n) =s f(n)+tg(n)也是这个递推的解。
回到斐波那契递推,从定理可知
是一个解,对于所有实数s,t。边界条件为f(0) =1且f(1) =1
22.3.2求解齐次线性递推
求解斐波那契递推的方法可以扩展适用于任意齐次线性递推,即形如
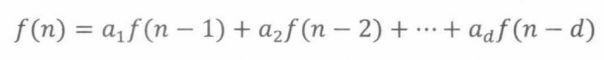
猜测 f ( n ) = x n f(n) = x^n f(n)=xn
化简得:
上式称为递推的特征方程。特征方程的根就是线性递推的解。如果不考虑边界条件:
解除特征方程的解之后,接下来,通过选择合适的常量,找出满足边界条件的解。
22.3.3求解一般线性递推
现在,我们可以求解所有的齐次线性递推了,形如
一般地,在等式右侧增加额外项g(n)的线性递推称为非齐次线性递推
求解非齐次线性递推,可以把整个过程分为5步:
1.用0替代g(n),得到一个齐次线性递推。如同之前一样,得到特征方程的根。
2.计算齐次递推的解,但是不要用边界条件去确定常量,这称之为齐次解
3.恢复g(n),忽略边界条件,确定一个递推解,称为特解。稍后将介绍如何确定特解。
4.将齐次解和特解加起来得到通解。
5.使用边界条件,求解线性方程组确定常量。
22.3.4 如何猜测特解
确定特解时,需要猜测,这里有一些猜测的经验。
- 一般来说,可以找一个与非齐次项g(n)具有相同形式的特解。
- 如果g(n)是常量,猜测特解f(n)= c。如果猜错了,依次尝试更高幂次的多项式:f(n) = bn +c,然后是f(n) = a n 2 n^2 n2 + bn +c,等等。
- 更一般地,如果g(n)是多项式,先尝试幂次相同的多项式,然后依次是更高一次的多项式,更高二次的多项式,等等。例如,如果g(n) = 6n +5,那么先尝试f(n)= bn + c,然后尝试f(n)= a n 2 n^2 n2+ bn +c。
- 如果g(n)是指数形式,例如 3 n 3^n 3n,先猜测f(n)= c 3 n 3^n 3n。如果错误,依次尝试f (n) = bn 3 n 3^n 3n+c 3 n 3^n 3n,然后是f(n) = a n 2 n^2 n2 3 n 3^n 3n + bn 3 n 3^n 3n + c 3 n 3^n 3n,等等。
22.4 分治递推
我们已经学会了一般线性递推的解法。但是前面提到的归并排序递推,并不是线性的。
对这类算法进行分析,通常就是分治递推,形式如下:
其中 a 1 , … , a k a_1,… ,a_k a1,…,ak是正常数, b 1 , … , b k b_1,…,b_k b1,…,bk是0到1之间的常数,g(n)是一个非负函数。
22.4.1 Akra-Bazzi公式
Akra-Bazzi公式给出了几乎所有分治递推的解。很简单,一般分治递推
的渐近解是
其中p满足
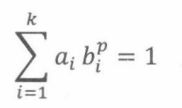
需要注意的是,函数g(n)不能增长得太快或者变化得太剧烈。确切地说,Ig’(n)|必须存在多项式界。例如,Akra-Bazzi 公式适用于g(n) = x 2 x^2 x2logn,而不适用于g(n)= 2 n 2^n 2n。
22.4.2两个技术问题
我们发现了分治递推的两个问题。
首先,Akra-Bazzi公式不能处理边界条件。
分治递推的近似解与边界条件无关。直觉告诉我们,如果一个递归算法的基本操作执行时间变为原来的2倍,总的运行时间也差不多要翻倍。在现实中这很重要,但是近似计算会忽略⒉这个因素。还有一些极端情况。例如,T(n)= 2T(n/2)的解是0(n)还是0取决于T(1)是不是0。
分治递推的第二个问题是不产生线性递推。即,对一个规模为n的问题进行分解,产生的子问题可能不是整数规模的。例如归并排序递推包含项T(n/2)。那么n = 15怎么办?
这个递推或许是严格准确的,但是向上取整和向下取整操作使这个递推很难得到精确解。
幸运的是,分治递归的近似解,不受向上取整和向下取整操作的影响。更准确地说,用T([ b i b_i bin])或T([ b i b_i bin])取代T([ b i b_i bin])并不会改变解。所以很多时候,将向上和向下取整操作从分治递推中去掉是合理的,它们复杂且没什么影响。
22.4.3Akra-Bazzi定理
Akra-Bazzi公式以及关于边界条件和取整的断言,都源于Akra-Bazzi定理。定理描述如下。当然,实际的归并排序会把输人近似地分为两半,递归地对这两半分别进行排序,然后合并结果。
定理22.4.1 (Akra-Bazzi)设函数T:R→R是非负的,当0≤x≤x时有界,且满足递推
其中:
那么:
其中p满足
Akra-Bazzi公式是直接从 Akra-Bazzi定理得出的,不过定理中的递推还有函数hi。这个函数能够处理向下取整、向上取整,以及对子问题的规模等的其他微调操作。
22.4.4主定理
Akra-Bazzi公式的一个特例称为主定理(Master Theorem ),可以用于计算机科学中一些常见的递推。
定理22.4.2(主定理)对于如下形式的递归T
22.5进─步探索
我们已经求解过以下几个的递推:
每个递推都有优点和缺点。在汉诺塔问题中,规模为n的问题被分解为两个规模为n- 1的子问题(较大),但是只需要1次额外操作(较少)。在归并排序中,规模为n的问题被分解为两个规模为n/2的子问题(较小),但是需要n- 1次额外操作(较多)。最后,归并排序的速度快得多!
这说明:将问题分解为更小规模的子问题,比减少每次递归调用的额外操作时间重要得多。
更一般地说,线性递推(具有较大的子问题)往往具有指数形式的解,而分治递推(具有较小的子问题)的解通常具有多项式界。
递推都有优点和缺点。在汉诺塔问题中,规模为n的问题被分解为两个规模为n- 1的子问题(较大),但是只需要1次额外操作(较少)。在归并排序中,规模为n的问题被分解为两个规模为n/2的子问题(较小),但是需要n- 1次额外操作(较多)。最后,归并排序的速度快得多!