随机游走问题的神奇应用(一)
泊松方程的随机游走求解
-
- 一.问题的提出
- 二.问题的求解
- 三.代码求解
可以用monteCarlo方法构建一个随机游走过程来求解偏微分方程。
一.问题的提出
求解二维泊松方程的第一边值问题如下:
∂ 2 u ( P ) ∂ x + ∂ 2 u ( P ) ∂ y 2 = q ( P ) P ( x , y ) ∈ D \frac{\partial^2 u(P)}{\partial x} + \frac{\partial^2 u(P)}{\partial y^2} = q(P)\quad P(x,y) \in D\\ ∂x∂2u(P)+∂y2∂2u(P)=q(P)P(x,y)∈D
边界条件为:
u ( Q ) = f ( Q ) Q ( x , y ) ∈ Γ = ∂ D u(Q) = f(Q)\quad Q(x,y)\in \Gamma = \partial D u(Q)=f(Q)Q(x,y)∈Γ=∂D
二.问题的求解
如下图所示如果我们要求在 P ( x ∗ , y ∗ ) P(x^*,y^*) P(x∗,y∗)处的值,设求解步长为 h h h。我们就将原来的方程差分化:
u ( x + h , y ) + u ( x − h , y ) − 2 u ( x , y ) h 2 + u ( x , y + h ) + u ( x , y − h ) − 2 u ( x , y ) h 2 = q ( x , y ) \frac{u(x+h,y)+u(x-h,y) -2u(x,y)}{h^2}+\frac{u(x,y+h)+u(x,y-h) -2u(x,y)}{h^2} = q(x,y) h2u(x+h,y)+u(x−h,y)−2u(x,y)+h2u(x,y+h)+u(x,y−h)−2u(x,y)=q(x,y)
可以化成如下差分形式:
u = − h 2 4 q + ∑ i = 1 4 u 1 i u = -\frac{h^2}{4}q+\sum_{i= 1}^4u_{1i} u=−4h2q+i=1∑4u1i
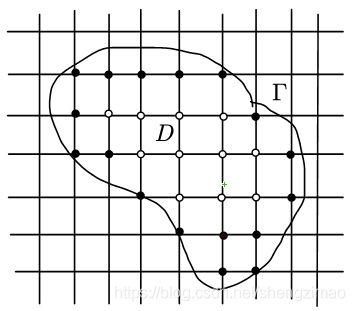
其中 P 1 i P_{1i} P1i的含义如下图所示:

我们假设方程的定义区域为下图,黑点为边界 Γ \Gamma Γ上的点,白点为内部 D D D上的点。
我们定义一个从 P ( x ∗ , y ∗ ) P(x^*,y^*) P(x∗,y∗)开始的游走路线:
ρ P : P → P 1 → P 2 → P 3 . . . → P k − 1 → Q ∈ Γ \rho_P :P\rightarrow P_1 \rightarrow P_2 \rightarrow P_3...\rightarrow P_{k-1}\rightarrow Q\in \Gamma ρP:P→P1→P2→P3...→Pk−1→Q∈Γ
其中的点 P i P_i Pi是由点 P i − 1 P_{i-1} Pi−1进过以下规则 f f f得到的:
f : P i − 1 → P i f:P_{i-1} \rightarrow P_i f:Pi−1→Pi
f f f:我们产生一个随机数 r ∈ [ 0 , 1 ] r\in[0,1] r∈[0,1]:
| r r r | P i − 1 P_{i-1} Pi−1 | P i P_i Pi |
|---|---|---|
| [ 0 , 0.25 ] [0,0.25] [0,0.25] | P i − 1 ( x ∗ , y ∗ ) P_{i-1}(x^*,y^*) Pi−1(x∗,y∗) | P i ( x ∗ + h , y ∗ ) P_i(x^*+h,y^*) Pi(x∗+h,y∗) |
| [ 0.25 , 0.5 ] [0.25,0.5] [0.25,0.5] | P i − 1 ( x ∗ , y ∗ ) P_{i-1}(x^*,y^*) Pi−1(x∗,y∗) | P i ( x ∗ , y ∗ + h ) P_i(x^*,y^*+h) Pi(x∗,y∗+h) |
| [ 0.5 , 0.75 ] [0.5,0.75] [0.5,0.75] | P i − 1 ( x ∗ , y ∗ ) P_{i-1}(x^*,y^*) Pi−1(x∗,y∗) | P i ( x ∗ − h , y ∗ ) P_i(x^*-h,y^*) Pi(x∗−h,y∗) |
| [ 0.75 , 1 ] [0.75,1] [0.75,1] | P i − 1 ( x ∗ , y ∗ ) P_{i-1}(x^*,y^*) Pi−1(x∗,y∗) | P i ( x ∗ , y ∗ − h ) P_i(x^*,y^*-h) Pi(x∗,y∗−h) |
表示 P i − 1 P_{i-1} Pi−1分别有 1 4 \frac{1}{4} 41的概率到 P 11 , P 12 , P 13 , P 14 P_{11},P_{12},P_{13},P_{14} P11,P12,P13,P14,即有相同的概率前后左右随机移动,到终点为止。
那么在这样的规则下会生成一条路线 ρ P \rho_P ρP。此时我们建立其以下的映射关系:
g : ρ p → u ( P ) g:\rho_p \rightarrow u(P) g:ρp→u(P)
即是从 P P P点出发的一条路线 ρ P \rho_P ρP到该点的数值解 u ( P ) u(P) u(P)的一个映射关系 g g g。
现在我们直接给出这个关系:
g : u ( P ) = − h 2 4 ∑ i = 1 k − 1 q ( P i ) + f ( Q ) g:u(P) = -\frac{h^2}{4}\sum_{i = 1}^{k-1}q(P_i)+f(Q) g:u(P)=−4h2i=1∑k−1q(Pi)+f(Q)
那么我们从这一次随机游走 ρ P \rho_P ρP映射出了一次的 u ( P ) u(P) u(P)。这个结果肯定是不精确的,我们如果设每次的结果都是一次随机变量 ζ P = g ( ρ P ) \zeta_P = g(\rho_P) ζP=g(ρP),那么可以证明的是 E ζ P = u ( P ) E\zeta_P = u(P) EζP=u(P),具体证明过程忽略。我们利用这个结论可以由大数定律:
u ( P ) ∼ 1 N ∑ i = 1 N ζ P i u(P) \sim\frac{1}{N}\sum_{i =1}^N\zeta_{Pi} u(P)∼N1i=1∑NζPi
即通过多次模拟随机游走的过程求其均值用来表示当前的解 u ( P ) u(P) u(P)。
三.代码求解
假设我们要求解的是以下方程:
∂ 2 u ∂ x + ∂ 2 u ∂ y 2 = 1 \frac{\partial^2 u}{\partial x} + \frac{\partial^2 u}{\partial y^2} =1 \\ ∂x∂2u+∂y2∂2u=1
边界 Γ : x 2 + y 2 = 2 \Gamma:x^2+y^2 =2 Γ:x2+y2=2。在此边界上:
u ( Γ ) = 1 2 u(\Gamma) = \frac{1}{2} u(Γ)=21
现求 u ( 0 , 1 ) u(0,1) u(0,1)的值。
理论上该方程的解析解为 u ( x , y ) = x 2 + y 2 4 u(x,y) = \frac{x^2+y^2}{4} u(x,y)=4x2+y2,因此 u ( 0 , 1 ) = 1 4 u(0,1) = \frac{1}{4} u(0,1)=41。在这里,我们给出求解该方程的函数并且显示当前的随机游走过程:
function [uFinal,zeta] = possionRandom(xPoint,yPoint,h,N)
%UNTITLED 求 Deltea u = 1;在u(x^2+y^2 = 2) = 0.5边界条件
% [xPoint,yPoint]表示该点坐标,h仿真步长,N仿真次数
q = @(x,y)1; % 函数
f = @(x,y)(0.5);
u = zeros(1,N);
for i = 1:N
sumV = 0;
xValue = xPoint;
yValue = yPoint;
P = [xValue ,yValue];
%以下是游走过程
while(1)
if (xValue)^2+(yValue)^2>=2
P = [P;xValue,yValue];
break;
end
randNumber = randsrc(1,1,[[0 1 2 3];[0.25 0.25 0.25 0.25]]);
switch (randNumber)
case 0
xValue = xValue + h;
yValue = yValue;
case 1
xValue = xValue ;
yValue = yValue + h;
case 2
xValue = xValue - h ;
yValue = yValue ;
case 3
xValue = xValue;
yValue = yValue - h;
end
P = [P;xValue,yValue];
end
%以下是画图过程
if i == 1
subplot(121);
grid on;
plot(P(:,1),P(:,2),'b.-');
title('第一次轨迹');
end
%以下是计算过程
[m,n] = size(P);
for j = 1:m-1
if isnan(q(P(j,1),P(j,2))) == 1
q(P(j,1),P(j,2)) = q(h,h);
end
sumV = sumV + q(P(j,1),P(j,2));
end
zeta(i) = -h^2/4*sumV + f(P(m,1),P(m,2));
u(i) = sum(zeta(1:i))/i;
end
subplot(122);
grid on ;
uFinal = u(N);
plot(1:N,u,'r');
xlabel('次数');
ylabel('进化曲线');
title('收敛过程');
end
在命令行求解 u ( 0 , 1 ) u(0,1) u(0,1)的值如下,设置步长为 h = 0.01 h = 0.01 h=0.01,仿真次数 N = 100 N = 100 N=100:
>> [uFinal,zeta] = possionRandom(0,1,0.01,100);
得到如下图形:
最终结果为 0.2353 0.2353 0.2353。可以发现还是有点误差的。
关键是这玩意如果步长设置的比较小的话就会一直游走。所以运行的时间就会比较长。