用深层神经网络识别猫咪图片：吴恩达Course1-神经网络与深度学习-week3&week4作业

代码有参考吴恩达老师的源代码，神经网络的图片为转载，图片来源见水印

以下文件的【下载地址】，提取码：dv8a

所有文件存放位置
C:.
│  dnn_utils.py
│  building deep neural network：step by step.py
│  lr_utils.py
│  testCases.py
│
├─datasets
        test_catvnoncat.h5
        test_image1.png
        test_image2.png
        train_catvnoncat.h5

---

一些要点

神经网络的层数：指隐藏层+输出层的层数
二层神经网络：有一个输入层、一个隐藏层、一个输出层的神经网络
L层神经网络：有一个输入层、L-1个隐藏层、第L层为输出层的神经网络

——假如对于每个隐藏层，我们都使用[线性传播+同一非线性函数激活]的方式，则构建L层神经网络，无非是将二层神经网络对隐藏层的运算，重复L-1次

深层网络的参数初始化方式不同于二层网络，网络层次越高，越容易产生梯度消失/梯度爆炸现象，这里对深层网络使用Xaiver初始化（在网上看到很多同学的cost卡在0.64降不下去就是这个坑）

---

---

深层网络的实现步骤

参数初始化-> [实现前向线性传播 -> 实现前向线性激活 -> 实现完整的前向传播] -> 计算成本 -> [实现反向线性传播 -> 实现反向线性激活 -> 实现完整的反向传播] -> 参数更新

这里会对比二层网络和深层网络的测试集准度，使用深层网络对本地图片进行识别

---

导入库

import numpy as np
from matplotlib import pyplot as plt
import testCases
from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward
import lr_utils
# 测试本地图片时使用
import imageio
import cv2

---

设置随机种子并初始化

np.random.seed(1)
# 初始化[二层神经网络]的参数
def initialize_parameters(n_x, n_h, n_y):
    """
    :param n_x: x的特征数量
    :param n_h: 隐藏层节点数量
    :param n_y: 输出层的特征数量
    """
    W1 = np.random.randn(n_h, n_x)*0.01
    b1 = np.zeros(shape=(n_h, 1))
    W2 = np.random.randn(n_y, n_h)*0.01
    b2 = np.zeros(shape=(n_y, 1))
    parameters = {'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}
    return parameters
# 初始化[深层神经网络]的参数
def initialize_parameters_deep(layer_dims):
    """
    :param layer_dims: 列表，从输入层至输出层，每层的节点数量
    """
    parameters = {}
    L = len(layer_dims) - 1                         # 输出层的下标
    for l in range(1, L+1):
        # 使用Xaiver初始化，防止梯度消失或爆炸
        parameters['W'+str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])/np.sqrt(layer_dims[l - 1])
        parameters['b'+str(l)] = np.zeros(shape=(layer_dims[l], 1))
    return parameters

---

前向传播

# 前向传播中的线性传播
def linear_forward(A_prev, W, b):
    """
    :param A_prev: 上一层传递到本层的A
    :param W: 本层的权重矩阵
    :param b: 本层的偏置项
    :return: 本层计算的Z
    """
    Z = np.dot(W, A_prev) + b
    cache = (A_prev, W, b)
    assert(Z.shape==(W.shape[0], A_prev.shape[1]))
    return Z, cache
# 前向传播中的线性激活
def linear_and_activation_forward(A_prev, W, b, activation='relu'):
    """
    :param activation: 字符串，激活函数名称
    """
    Z, linear_cache = linear_forward(A_prev, W, b)

    # 按激活函数执行激活步骤
    if activation == 'sigmoid':
        A, activation_cache = sigmoid(Z)            # 缓存的是Z
    elif activation == 'relu':
        A, activation_cache = relu(Z)

    assert(A.shape==Z.shape)
    cache = (linear_cache, activation_cache)
    return A, cache
# 完整的前向传播
def L_model_forward(X, parameters):
    caches = []
    A = X
    L = len(parameters)//2
    # 计算隐藏层
    for l in range(1, L):
        A, cache = linear_and_activation_forward(A, parameters['W'+str(l)], parameters['b'+str(l)], 'relu')
        caches.append(cache)
    # 计算输出层
    AL, cache = linear_and_activation_forward(A, parameters['W'+str(L)], parameters['b'+str(L)], 'sigmoid')
    caches.append(cache)

    assert(AL.shape==(1, X.shape[1]))                       # 2分类时输出层特征数是1
    return AL, caches

---

计算成本

# 计算成本
def compute_cost(AL, Y):
    m = Y.shape[1]
    # 计算交叉熵
    cost = -1/m * np.sum(Y*np.log(AL)+(1-Y)*np.log(1-AL))
    assert(isinstance(cost, float))
    return cost

---

反向传播

# 反向传播中的线性传播
def linear_backward(dZ, cache):
    m = dZ.shape[1]
    # 解压前向线性传播的cache
    A_prev, W, b = cache
    # 计算偏导数
    dW = 1/m * np.dot(dZ, A_prev.T)                         # nl x m * m x nl-1 = nl x nl-1
    db = 1/m * np.sum(dZ, axis=1, keepdims=True)            # nl x 1
    dA_prev = np.dot(W.T, dZ)                               # nl-1 x m

    assert(dW.shape==W.shape)
    assert(db.shape==b.shape)
    assert(dA_prev.shape==A_prev.shape)
    return dA_prev,dW,db
# 反向传播中的线性激活
def linear_and_activation_backward(dA, layer_cache, activation='relu'):
    # 解压cache
    linear_cache, activation_cache = layer_cache
    # 计算dZ
    if activation=='relu':
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    elif activation=='sigmoid':
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    return dA_prev, dW, db
# 完整的反向传播
def L_model_backward(AL, Y, caches):
    grads = {}
    L = len(caches)                                             # 输出层的下标
    Y = Y.reshape(AL.shape)

    # AL关于L的偏导数
    dAL = -np.divide(Y, AL) + np.divide(1-Y, 1-AL)              # 对应元素相除
    layer_cache = caches[L-1]
    # 用dAL计算dAL-1，dWL，dbL
    grads['dA'+str(L-1)], grads['dW'+str(L)], grads['db'+str(L)] = linear_and_activation_backward(dAL, layer_cache, 'sigmoid')

    # 计算输入层参数关于L的偏导数
    for l in reversed(range(L-1)):                              # 范围是L-2至0
        layer_cache = caches[l]
        # 用dAl计算dAl-1，dWl，dbl
        dAl = grads['dA'+str(l+1)]
        grads['dA'+str(l)], grads['dW'+str(l+1)], grads['db'+str(l+1)] = linear_and_activation_backward(dAl, layer_cache, 'relu')
    return grads

---

参数更新

# 更新参数
def update_parameters(parameters, grads, learning_rate):
    L = len(parameters)//2
    for l in range(1, L+1):
        parameters['W'+str(l)] -= learning_rate*grads['dW'+str(l)]
        parameters['b'+str(l)] -= learning_rate*grads['db'+str(l)]
    return parameters

---

整合完整模型-L层神经网络

# L层神经网络的完整模型，它的流程为：INPUT-> [LINEAR-> ReLU->...] 重复L-1次  -> LINEAR -> Sigmoid -> OUTPUT
def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False):
    """
    :param layers_dims: 元组/列表，从输入层至输出层的节点数
    :param print_cost: 是否打印cost值
    :return: 字典，所有Wl，bl, l in [1, L]
    """
    np.random.seed(1)
    costs = []
    # 计算神经网络层数
    L = len(layers_dims)-1

    # 如果层数小于3，初始化[二层神经网络]的参数；否则，初始化[深层神经网络]的参数
    if L < 3:
        n_x, n_h, n_y = layers_dims
        parameters = initialize_parameters(n_x, n_h, n_y)
    else:
        parameters = initialize_parameters_deep(layers_dims)

    # 进入迭代
    for i in range(num_iterations+1):
        # 前向传播计算AL
        AL, caches = L_model_forward(X, parameters)
        # 计算成本
        cost = compute_cost(AL, Y)
        # 反向传播，计算各参数关于成本函数的偏导数
        grads = L_model_backward(AL, Y, caches)
        # 更新参数
        parameters = update_parameters(parameters, grads, learning_rate)

        # 每100次迭代标记一次cost
        if print_cost and i % 100 == 0:
            print('Cost after iteration {}: {}'.format(i, cost))
            costs.append(cost)

    plt.plot(costs, '.-')
    plt.xlabel('iterations per 100')
    plt.ylabel('cost')
    plt.title('Learning rate =' + str(learning_rate))
    plt.show()
    return parameters

---

预测y值

# 预测函数
def predict(X, Y, parameters):
    L = len(parameters)//2
    m = X.shape[1]

    # 计算AL
    AL, cache = L_model_forward(X, parameters)
    # 计算预测值^Y
    Y_predict = np.round(AL)

    # 计算准确率
    accuracy = np.sum(Y_predict == Y) / m * 100
    print('Accuracy is: %.2f%%' % accuracy)
    return Y_predict

---

载入训练集和测试集

# 载入数据集
train_x_orig, train_y, test_x_orig, test_y, classes = lr_utils.load_dataset()
# train_x_orig的维度(209, 64, 64, 3) 表示(样本量，高度，宽度，颜色通道个数)

# 可视化其中一个图片
plt.imshow(train_x_orig[10])
print('y = ' + str(train_y[0, 10]) + '. It is a ' + classes[train_y[0, 10]].decode('utf-8') + ' picture.')
plt.show()
# 这是一张小鸟图

y = 0. It is a non-cat picture.

# 采集维度数据
m_train = train_x_orig.shape[0]                                   # 训练样本量
num_px = train_x_orig.shape[1]                                    # 图片宽度/高度，两者相等
m_test = test_x_orig.shape[0]                                     # 测试样本量

# 展平训练集和测试集，神经网络模型采用(特征数，样本数)形状的训练集
train_x_flatten = train_x_orig.reshape(m_train, -1).T             # 一样本为一列
test_x_flatten = test_x_orig.reshape(m_test, -1).T
# 进行归一化，把数据缩放至0-1
train_x = train_x_flatten/255
test_x = test_x_flatten/255
print('shape of train_x', train_x.shape)
print('shape of test_x', test_x.shape)

# 设置输入层和输出层的节点数量
n_x = num_px * num_px * 3
n_y = 1

行表示图片节点数（特征数），列表示样本量：

shape of train_x (12288, 209)
shape of test_x (12288, 50)

---

创建一个二层神经网络

# 创建一个二层神经网络
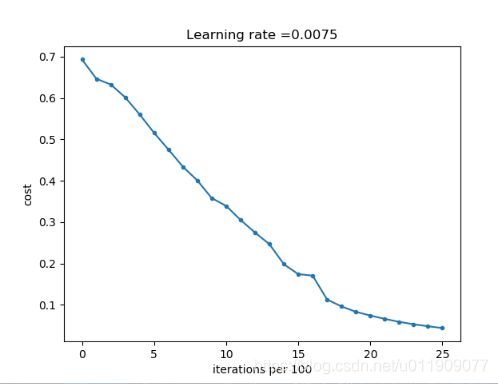
parameters = L_layer_model(train_x, train_y, layers_dims=(n_x, 7, n_y), num_iterations=2500, print_cost=True)
# 训练集准确率
predict_train_y = predict(train_x, train_y, parameters)
# 测试集准确率
predict_test_y = predict(test_x, test_y, parameters)

2500次迭代后，成本收敛至0.04附近：

Cost after iteration 0: 0.693049735659989
Cost after iteration 100: 0.6464320953428849
Cost after iteration 200: 0.6325140647912677
Cost after iteration 300: 0.6015024920354666
Cost after iteration 400: 0.5601966311605747
Cost after iteration 500: 0.5158304772764729
Cost after iteration 600: 0.4754901313943325
Cost after iteration 700: 0.43391631512257495
Cost after iteration 800: 0.4007977536203887
Cost after iteration 900: 0.35807050113237976
Cost after iteration 1000: 0.3394281538366413
Cost after iteration 1100: 0.30527536361962654
Cost after iteration 1200: 0.2749137728213015
Cost after iteration 1300: 0.24681768210614846
Cost after iteration 1400: 0.19850735037466097
Cost after iteration 1500: 0.17448318112556663
Cost after iteration 1600: 0.17080762978096892
Cost after iteration 1700: 0.11306524562164715
Cost after iteration 1800: 0.09629426845937145
Cost after iteration 1900: 0.08342617959726861
Cost after iteration 2000: 0.07439078704319078
Cost after iteration 2100: 0.06630748132267933
Cost after iteration 2200: 0.05919329501038171
Cost after iteration 2300: 0.05336140348560554
Cost after iteration 2400: 0.04855478562877018
Cost after iteration 2500: 0.0441405969254878

训练集和测试集的准确率为100%和72%：

Accuracy is: 100.00%
Accuracy is: 72.00%

下面建立深层模型，看测试集准度能否改善

---

创建一个深层神经网络

# 创建一个四层神经网络
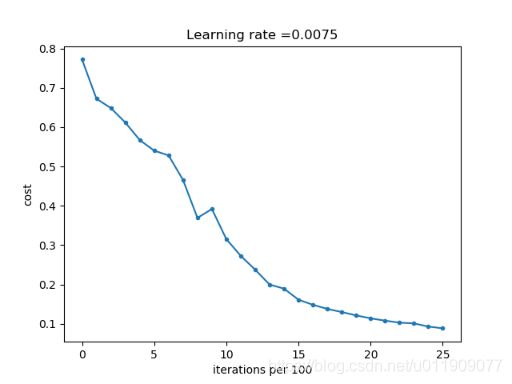
parameters = L_layer_model(train_x, train_y, layers_dims=(n_x, 20, 7, 5, n_y), num_iterations=2500, print_cost=True)
# 训练集准确率
predict_train_y = predict(train_x, train_y, parameters)
# 测试集准确率
predict_test_y = predict(test_x, test_y, parameters)n_x

用相同的迭代次数和学习率训练，2500次迭代后，成本收敛至0.08附近：

Cost after iteration 0: 0.7717493284237686
Cost after iteration 100: 0.6720534400822913
Cost after iteration 200: 0.6482632048575212
Cost after iteration 300: 0.6115068816101354
Cost after iteration 400: 0.567047326836611
Cost after iteration 500: 0.5401376634547801
Cost after iteration 600: 0.5279299569455267
Cost after iteration 700: 0.46547737717668514
Cost after iteration 800: 0.369125852495928
Cost after iteration 900: 0.39174697434805344
Cost after iteration 1000: 0.3151869888600617
Cost after iteration 1100: 0.27269984417893856
Cost after iteration 1200: 0.23741853400268131
Cost after iteration 1300: 0.19960120532208647
Cost after iteration 1400: 0.18926300388463305
Cost after iteration 1500: 0.1611885466582775
Cost after iteration 1600: 0.14821389662363316
Cost after iteration 1700: 0.13777487812972944
Cost after iteration 1800: 0.1297401754919012
Cost after iteration 1900: 0.12122535068005212
Cost after iteration 2000: 0.11382060668633712
Cost after iteration 2100: 0.10783928526254132
Cost after iteration 2200: 0.10285466069352679
Cost after iteration 2300: 0.10089745445261786
Cost after iteration 2400: 0.09287821526472395
Cost after iteration 2500: 0.0884125117761504

深层网络将测试准度从72%提高至80%，改善效果较明显

Accuracy is: 98.56%
Accuracy is: 80.00%

---

分析误分类图片

# 打印错误分类的图片
def print_mislabeled_image(classes, X, Y, Y_predict):
    # 误分类的切片；只给np.where输入条件，则返回tuple，元素一为0数组，元素二为满足条件的index数组，也可使用np.nonzero
    mislabeled_indices = np.where(Y!=Y_predict)[1]

    # 画图
    num_images = len(mislabeled_indices)
    plt.rcParams['figure.figsize'] = (100, 100)               # 图像显示的默认大小
    for i in range(num_images):
        index = mislabeled_indices[i]
        plt.subplot(2, num_images//2+1, i+1)
        plt.imshow(X[:, index].reshape(num_px, num_px, 3))
        plt.axis('off')
        plt.title('Prediction: ' + classes[int(Y_predict[0, index])].decode('utf-8') + '\n' +
                  'Class: ' + classes[int(Y[0, index])].decode('utf-8'))
    plt.show()
print_mislabeled_image(classes, test_x, test_y, predict_test_y)

观察上面的图片，导致分类错误的原因可能包括：
1.非猫图片出现了类似猫的纹理和形状（如蝴蝶的颜色和猫纹理相似，翅膀与猫耳朵形状相似）
2.猫图片的特征缺失（如不完整的猫脸）
3.猫与背景颜色相近
4.猫的形态较罕见（角度、姿势、身体出现在图片中的比例、位置等）
5.图片的复杂度
6.猫的品种
7.尺寸变化

---

用深层网络识别本地猫图

我们现在拥有一个准度可观的深层模型
用它识别以下这两张本地图片，看看它表现如何吧？

# 识别本地猫咪图片
def test_local_picture(img_path, num_px, y, parameters, classes):
    print('------------------')
    # 读取一张图片
    image = np.array(imageio.imread(img_path))
    # 改变图像至指定尺寸。只保留resize()输出的前3列，为rgb通道数值；第4列为值255
    image_cut = cv2.resize(image, dsize=(num_px, num_px))[:, :, :3].reshape(-1, 1)
    # 归一化图像数据
    test_x = image_cut/255
    # 预测分类
    test_y = np.array(y).reshape(1, 1)
    y_predict = predict(test_x, test_y, parameters)
    # 打印结果
    print('y = ' + str(y) + '. Predicted a ' + classes[int(np.squeeze(y_predict))].decode('utf-8') + ' picture.')

# 测试一张本地的非猫图片
img_path1 = 'datasets/test_image1.png'
test_local_picture(img_path1, num_px, 0, parameters, classes)
# 测试一张本地的猫图片
img_path2 = 'datasets/test_image2.png'
test_local_picture(img_path2, num_px, 1, parameters, classes)

以下结果说明两张图片都被正确分类了，可喜可贺

------------------
Accuracy is: 100.00%
y = 0. Predicted a non-cat picture.
------------------
Accuracy is: 100.00%
y = 1. Predicted a cat picture.

---

一些延伸

这是一个比较粗糙的深层网络模型，虽然达到了不错的准度，但优化空间很大
可能的优化方向包括但不仅限于：
1.针对容易误判的情况扩大训练集
2.使用交叉验证的方式提高泛化能力
3.使用网格搜索等方法调整超参数
4.使用更复杂的网络结构

其他的以后学到再补充吧，感谢阅读！