因果6-估计因果效应

图1. 识别-估计流程

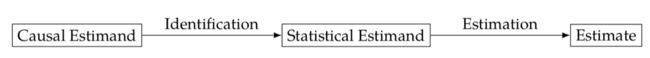
如图1所示，前两章我们学习了如何识别因果效应，将因果量转化为统计量，这一章我们学习如何估计因果效应。

首先回忆下之前学过的相关概念。

ITE(individual treatment effect):

个体因果效应。

$ITE=Y_i(1)-Y_i(0)$

ATE(average treatment effect)：

平均因果效应

$ATE=E[Y_i(1)-Y_i(0)]$

CATE(conditional average treatment effect):

条件平均因果效应，ATE对应的是 whole population, CATE对应的是 subpopulation。

$CATE=E[Y(W=1)|X=x]-E[Y(W=0)|X=x]$

在本章我们默认只考虑可识别情况，即都满足unconfoundedness和positivity。

COM（conditional outcome modeling，条件结果建模）

图2. 直观的建模想法

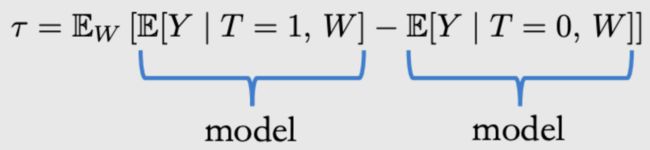
根据调整公式可得，

$\tau =E[Y(1)-Y(0)]=E_W[E[Y|T=1,W]-E[Y|T=0,W]]$，为了估计因果效应，最直接的想法是对图2所示的两个期望建模，具体模型可以是各种方法，比如线性回归，神经网络。

图3. 建模后的模型

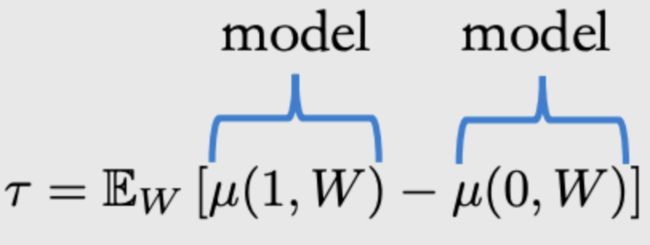
建模后的公式可转化为如图3所示的形式，进一步转化，可以得到

ATE COM Estimator:$\hat{\tau }=\frac{1}{n}{\sum }_i(\hat{\mu }(1,w_i)-\hat{\mu }(0,w_i))$

i表示每个样本,n表示样本数。

这是ATE的表达式，我们还可以进一步推到CATE的表达式：

$\mu (t,w,x)=E[Y|T=t,W=w,X=x]$（W是调整集合，X是子组依赖的变量，即CATE的condition）

CATE COM Estimator：$\hat{\tau }(x)=\frac{1}{n_x}{\sum }_{i:x_i=x}(\hat{\mu }(1,w_i,x)-\hat{\mu }(0,w_i,x))$

Problem with COM estimation in high dimensions

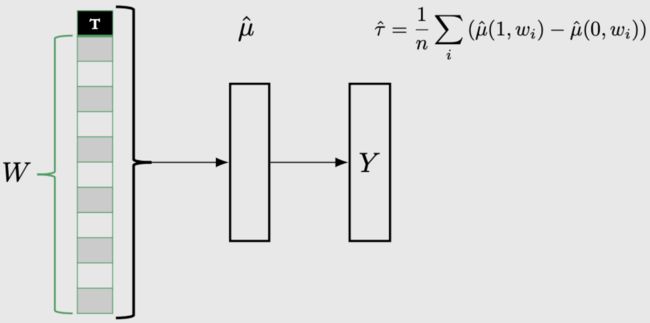
这种简单的COM模型在高维时会遇到一个问题，如图4所示，假如我们将T和W输入模型进行拟合，这时就会主线一个问题，T是1维的，相对于高维的W，在模型拟合中很容易被忽略。这样得到的$\hat{\tau }$会逼近于0.

图4. COM在高维中的问题

Grouped COM（GCOM） estimation

为了解决上述问题,GCOM提出一个简单的策略，如图5所示，直接用两个模型${\mu }_0$和${\mu }_1$分别拟合T=1和T=0的两组数据。

图5. GCOM

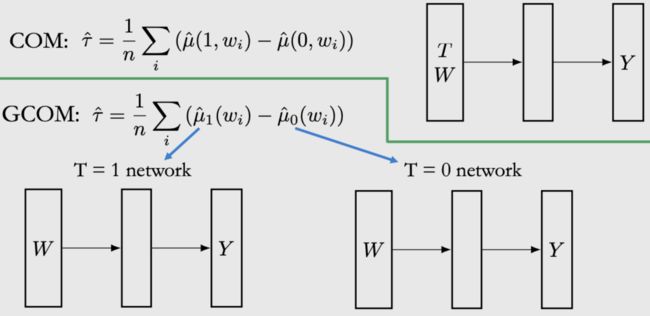
这样做的问题是，在${\mu }_1$模型中没有使用T=0的数据，而在${\mu }_0$模型中，也没使用T=1的数据，得到的结果$\hat{\tau }$会有很大方差。

Increasing Data Efficiency

为了更好地利用全部数据，我们继续学习两个算法。

TARNet

TARNet总结COM和GCOM的情况，选择先根据W数据拟合模型，然后分两个小子网络，分别值拟合T=0和T=1的数据，如图6所示，

图6. TARNet

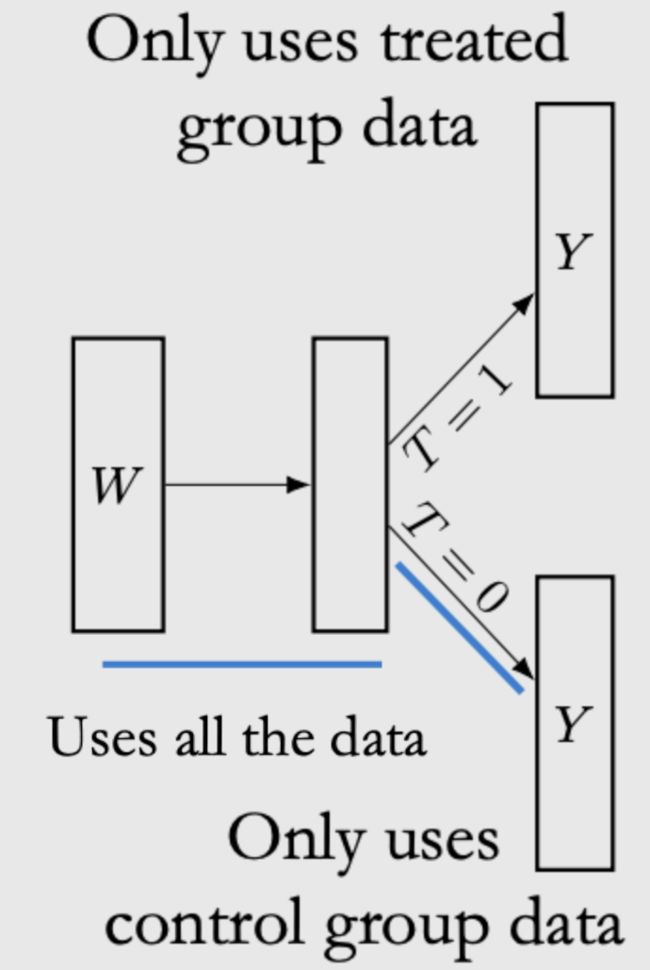
这个模型虽然相对于COM提高了数据的利用效率，但在子网络中还是没有用到全部的数据。

X-Learner

X-Learner为了提高数据利用效率，首先，估计${\hat{\mu }}_1(x)$和${\hat{\mu }}_0(x)$（类似GCOM的第一步）然后，不像GCOM直接分组估计，而是利用第一步得到的两个函数与数据再进一步结合，计算ITES，处理组：${\hat{\tau }}_{1,i}=Y_i(1)-{\hat{\mu }}_0(x_i)$，对照组：${\hat{\tau }}_{0,i}={\hat{\mu }}_1(x_i)-Y_i(0)$。这样得到的$\tau$便嵌入了整个数据的信息，最后对学到的$\tau$进行re-weighint，完整的流程如图7所示。

图7. X-Learner

这个模型有个很有趣的一点，就是他拿对于x的propensity score 对x的函数 $\tau (x)$进行balance，这背后隐藏一个假设，那就是$\tau (x)$函数没有改变其confounding bias的关系。

那么在表征学习中，可不可以也假设经过卷积网络的表征，也可以进行blance confounder bias？比如10个原型，我们设其他9个原型为X，剩下一个原型为T，然后计算T对结果的因果效应？

图7的末尾提到了 propensity score，我们来学习一下。

Propensity Score

倾向得分，其目的很简单，通过分配权重使数据满足unconfoundedness。

$e(W)\triangleq P(T=1|W)$

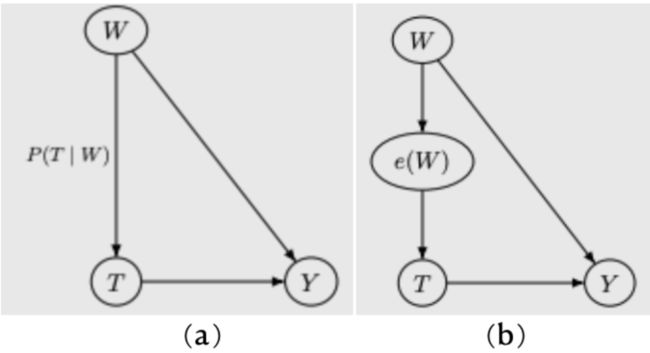
由此可得到倾向得分理论，这个方法的重点在于用一个标量e(W)替换了高维向量W。如图8所示，W对T的效应的分布就是P(T|W)，那么直接用一个函数e(W)去拟合P(T|W），就可以直接用标量e(W)替换W了。

换句话说，就是如果W可以block T 到 Y 的后门路径，那么e(W）也可以。

更正式的定义如下：

Propensity Score Theorem

如果W满足positivity和unconfoundedness，则

$(Y(1),Y(0))\perp \perp T|W=>(Y(1),Y(0))\perp \perp T|e(W)$

这个在观察性研究中该怎么证明？

图8. propensity score

如果大家还记得第2章的内容，会发现e(W)还有一个好处，就是他的降维提高了positivity的能力。

Inverse Probability Weighting（IPW)

图9. IPW Intuition

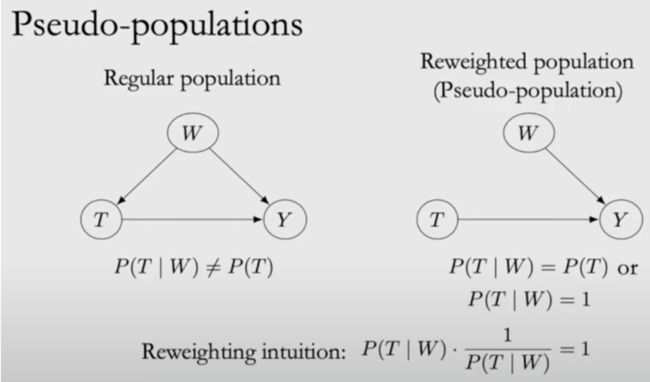
Also named as IPTW(inverse probability of treatment weighting).

$\tau \triangleq E[Y(1)-Y(0)]=E[\frac{1(T=1)Y}{e(W)}]-E[\frac{1(T=0)Y}{1-e(W)}]$

$\hat{\tau }=\frac{1}{n_1}{\sum }_{i:t_i=1}\frac{y_i}{\hat{e}(w_i)}-\frac{1}{n_0}{\sum }_{i:t_i=0}\frac{y_i}{1-\hat{e}(w_i)}$

该方法主要有两个缺点，

1. 其过度依赖于倾向值得分，e(x)出现一点偏差，ipw的误差就会急剧增大。为了解决这个问题，可以有两种方法：

   1. 在e(x)偏差时进行弥补（如对结果回归调整，DR)

   2. 提高对e(x)估计自身的robust（CBPS)。

2. 当倾向得分过小时，IPW会变得很不稳定。

Other methods

Doubly robust methods（DR）:结合COM和Propensity Score

Matching；double machine learning；causal trees and forests

Reference

Introduction to Causal Inference