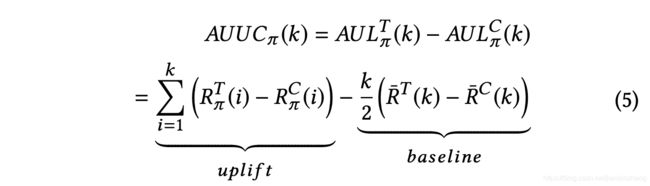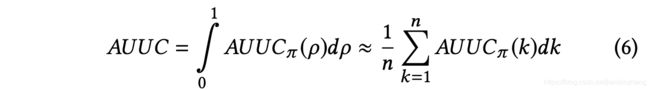【Uplift】评估方法篇
https://zhuanlan.zhihu.com/p/363082639
文章目录
-
- 线上评估方法
- 离线评估方法
-
- Uplift decile charts
- Cumulative uplift/gain
- Uplift Curve & AUUC
- Qini Curve & Qini Coefficient
- 补充,AUUC和Qini的另一种口径
- 参考文献
和标准的预测方法不同,由于”反事实“的存在,并没有真实的uplift标签,因此uplift模型无法在样本维度上进行评估。但如果有随机试验采集的数据,则可以用平均水平来评估uplift模型的效果。
本文将分为线上评估和离线评估两部分介绍,其中线上评估主要是AB策略;离线评估是AUUC、Qini等。
线上评估方法
最好的验证模型或策略效果的方法就是做线上的AB实验。在设计AB实验对比时,要小心处理目标的数据范围,在什么节点进行分流。
如果我们想知道的是全局的策略效果,则要在一开始就分流;而如果想知道策略生效部分的效果,则要在策略判定之后,对判定生效的部分进行分流,其中A桶原样返回,B桶生效返回。
下面是腾讯广告做uplift分析的流程图示例,通过线上AB试验的方式给出增量效果。
离线评估方法
线上评估虽然准确,但我们也需要具备离线评估的能力,避免浪费线上流量。与线上评估看整体的增量不同,离线评估需要能支持模型的效果对比。
离线评估方法有很多种,都需要对数据做分组(或累积)。将所有样本按照模型给出的uplift得分降序排列,按照等比分为K组(bins),后续的效果评估则通过对比相应组内Treatment组和Control组的得分差异实现。
Uplift decile charts
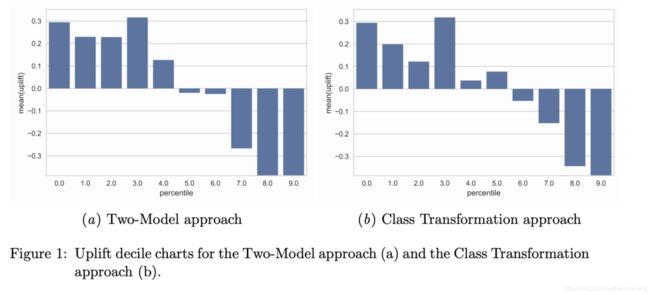
用第k组内Treatment和Control样本的 y ˉ \bar{y} yˉ之差表示,如下图表示按照uplift得分降序排列后,前50%的样本Treatment是正效果的,而后50%是负效果。
该方法虽然直观,但很难用于进行模型间的对比,如难以说明下面两个模型的优劣。
Cumulative uplift/gain
Cumulative uplift:通过计算topK组内Treatment和Control组的 y ˉ \bar{y} yˉ差值,可以表达在topK组得分的数据内,增量效果如何。如左图。
Cumulative gain:一些场景中,我们需要的不只是按照”uplift“选中部分的效果,而需要的是根据”uplift“来决策是Treat还是Control之后,能够带来的增量绝对量有多少。如右图,此时选择最高点即为最佳效果,再往后的实际是Control组优于Treatment组的部分。
公式如下, Y Y Y表示分组正例数量, N N N表示分组总量, ⋅ T \cdot^T ⋅T表示Treatment组, ⋅ C \cdot^C ⋅C表示Control组。
( Y T N T − Y C N C ) ( N T + N C ) \left(\frac{Y^{T}}{N^{T}}-\frac{Y^{C}}{N^{C}}\right)\left(N^{T}+N^{C}\right) (NTYT−NCYC)(NT+NC)
Uplift Curve & AUUC
上述方法还缺乏有效的度量手段,我们将数据集分组不断细分,精确到每个样本维度时,每次计算截止前t个样本的增量时,则得到Uplift Curve。公式如下
f ( t ) = ( Y t T N t T − Y t C N t C ) ( N t T + N t C ) f(t)=\left(\frac{Y_{t}^{T}}{N_{t}^{T}}-\frac{Y_{t}^{C}}{N_{t}^{C}}\right)\left(N_{t}^{T}+N_{t}^{C}\right) f(t)=(NtTYtT−NtCYtC)(NtT+NtC)
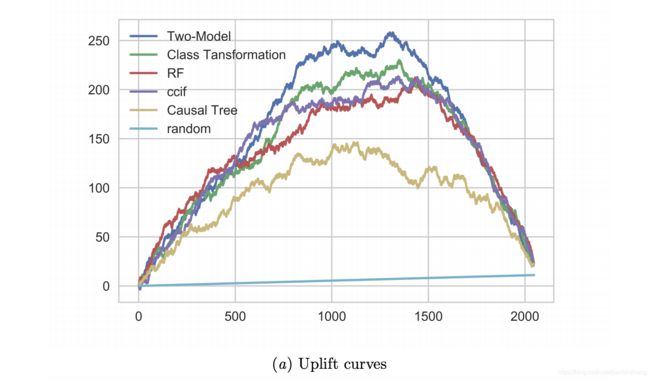
可视化如下,其中x轴为样本位序,y轴为累积增量数量。上方的每条曲线表示按照uplift score降序排列后,累积的增量效果;random直线表示随机排序(随机选择样本执行Treatment时)的增量效果;每条曲线终点相交,表示全量Treatment时的平均增量效果。
曲线中,越高拱的模型效果越好,数值化表示的话可以使用曲线下面积,与二分类评估中的AUC(Area Under ROC Curve)类似。这里称为AUUC(Area Under Uplift Curve),即 ∑ t N f ( t ) \sum_t^N f(t) ∑tNf(t)。
Qini Curve & Qini Coefficient
上述Uplift Curve存在一个问题,当Treatment组和Control组样本不一致时,其表达的增量存在偏差。因此对上式做一个缩放修改,相当于以Treatment组的样本量为准,对Control组做一个缩放,累积绘制的曲线称为Qini 曲线。
g ( t ) = Y t T − Y t C N t T N t C g(t)=Y_{t}^{T}-\frac{Y_{t}^{C} N_{t}^{T}}{N_{t}^{C}} g(t)=YtT−NtCYtCNtT
此时有 f ( t ) = g ( t ) N t T + N t C N t T f(t)=g(t)\frac{N_t^T+N_t^C}{N_t^T} f(t)=g(t)NtTNtT+NtC。
另外,取Qini曲线先面积为Qini系数。
补充,AUUC和Qini的另一种口径
前述的AUUC和Qini系数取自综述论文,CausalML的复现是基于这种的。在另一篇更新的论文中,明确提到了AUUC和Qini系数的计算公式,更复杂,似乎更合理,可以参考选用。其中的”uplift“部分当k取N时,实际上与前述的相同。
AUUC:
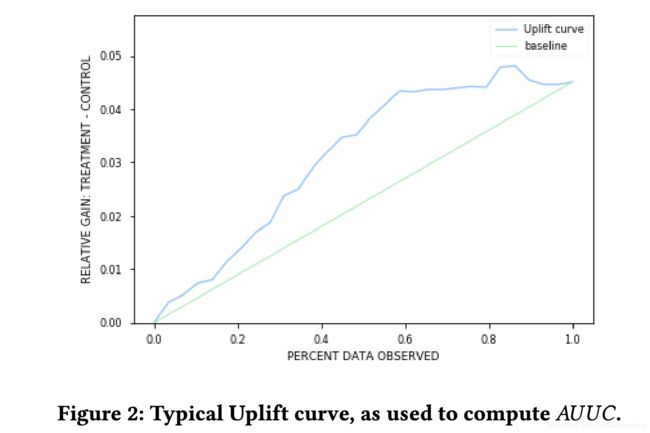
下图展示了一个Uplift曲线(这里目测除以总量了)
则AUUC定义为Uplift曲线和Baseline的曲线下面积差。第一项表示uplift曲线下面积,用累积求和表示;第二项表示baseline曲线下面积,用三角形面积公式表示。
其中 A U U C π ( k ) AUUC_\pi(k) AUUCπ(k)表示前k个样本计算得到的AUUC原子, A U L AUL AUL表示Area Under Lift, R π ( k ) = ∑ d i ∈ π ( k ) 1 [ y i = 1 ] R_{\pi}(k)=\sum_{d_{i} \in \pi(k)} \mathbb{1}\left[y_{i}=1\right] Rπ(k)=∑di∈π(k)1[yi=1]表示前k个样本中的正例数, R ˉ ( k ) = k ⋅ E [ Y ∣ T ∈ { 1 , 0 } ] \bar{R}(k)=k\cdot \mathbb{E}[Y|T\in\{1,0\}] Rˉ(k)=k⋅E[Y∣T∈{1,0}]表示前k个样本中的平均正例数。
取AUUC值为各个原子的均值,如下:
Qini coefficient:
Qini系数是Gini系数的一般化形式,与AUUC计算类似。首先由Qini曲线如下图,其中x轴表示数量,y轴表示增量数量。Qini原子的公式如下
公式的第一部分同上述的Qini曲线,是对以Treatment为标准做了缩放。第二部分用三角形面积公式计算,表示随机排序的结果。另外,如下图所示,best model表示理想情况下的曲线形式,从0开始,首先是45°提升(表示T组选中正例,而C组均是反例),接着是水平线(表示T组C组都是反例),最后45°下降(表示T组选中反例,而C组均是正例)。
此时,Qini系数如下,其中 π ∗ \pi^* π∗表示最优的排序。
另外,本文介绍了Qini系数相对AUUC的好处:①Qini系数做了T组和C组的样本缩放,解决AUUC在T组比C组多很多时不适用的问题;②Qini系数是归一化后的,这样它就可以在不同的数据集间做一个对比。
参考文献
[1]Causal Inference and Uplift Modeling A review of the literature
[2]A Large Scale Benchmark for Uplift Modeling
[3]更多参考:https://zhuanlan.zhihu.com/p/358582762