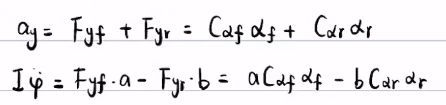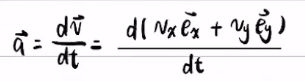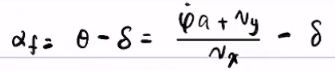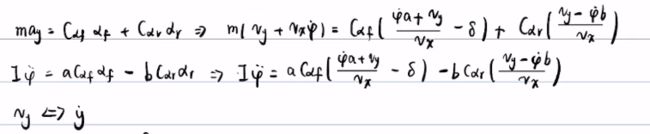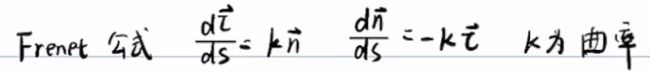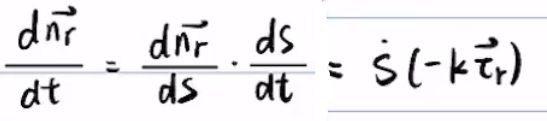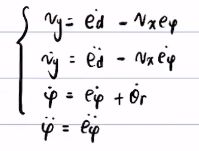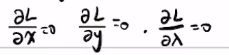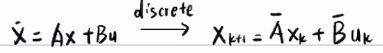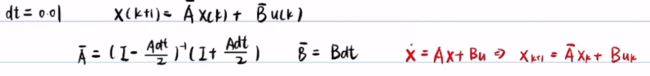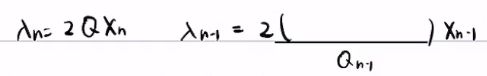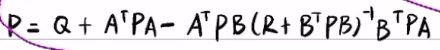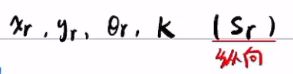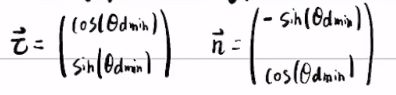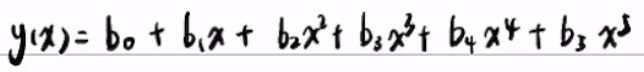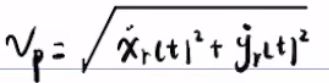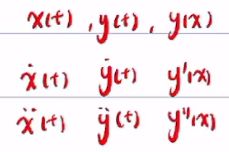【自动驾驶】【零基础】基础自动驾驶控制算法笔记

本文接近25000字

从理论到实践，全部零基础开始，一步一步完成自动驾驶车辆控制基础

感谢：忠厚老实的老王

下面是他的主页：忠厚老实的老王的个人空间_哔哩哔哩_bilibili

目录

第一讲  绪论

第二讲  三个坐标系与运动学方程

一、控制原理

二、三个坐标系

三、左手系与右手系

四、自行车模型的运动学方程

第三讲 轮胎侧偏与车辆动力学方程

一、动力学方程与Frenet坐标系解耦

二、轮胎的侧偏特性

三、考虑轮胎侧偏特性的自行车模型

第四讲 坐标变换与横向误差微分方程

第五讲 连续方程的离散化与离散LQR原理

一、离散化模型

 二、求解lqr

三、黎卡缇方程

四、总结

第六讲 前馈控制与航向误差

一、前馈控制

第七讲 离散规划轨迹的误差计算

一、离散的轨迹点的误差计算

第八讲

一、横向控制算法与流程图

（1）算法输入输出过程

（2）流程图

 （3）具体算法

 （4）预测模块

二、CarSim与Matlab联合仿真基础

三、代码与模型

第九讲  纵向控制开篇

一、纵向控制逻辑

二、发动机与变速器

三、CarSim基础设置

第十讲 油门刹车标定表的制作

一、理论部分

二、油门标定表制作

三、刹车标定表制作

第十一讲 纵向双PID控制

一、前置准备

二、油门和刹车标定表制作

三、纵向速度PID控制仿真

第十二讲  横纵向综合控制完结

一、规划接口

二、代码实践部分

三、转向不足

---

第一讲  绪论

请用谨慎，批判 ，怀疑的态度去研究自动驾驶的相关资料文献

新技术往往带有模糊和争议，自动驾驶是新技术，也不能避免

工具：google，Github

软件：matlab（2018a）、Carsim 2016、ROS、Linux

书：《无人驾驶车辆模型预测控制》龚建伟（第二版）（第一版很多错误） 

《车辆动力学及控制》=>《Vehicle Dynamics and Control》R.R. （百度Apollo）

自动驾驶技术：感知->决策->路径规划->控制

感知与决策难，控制难在调参，主要算法为PID，LQR，MPC

芯片计算速度（台式机性能的芯片）车载芯片工作环境极为恶劣

第二讲  三个坐标系与运动学方程

控制的前提是路径规划，默认已经有路径规划的储备知识

一、控制原理

油门/刹车 -> 力 -> 加速度 -> 速度 -> 位置（纵向控制）

方向盘 -> 前轮转角 -> 横向位移/航向角（横向控制）

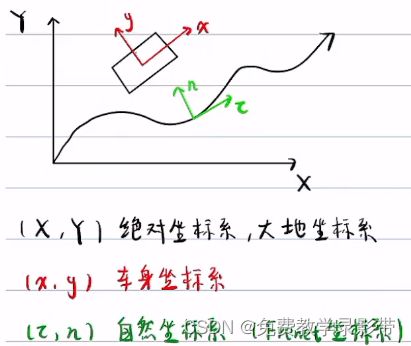
二、三个坐标系

 Frenet坐标系优点是：可以把纵向控制和横向控制解耦，减少计算量

车身坐标系与自然坐标系转换会难一些

三、左手系与右手系

一般数学，物理学是右手系。计算机图形，视觉为左手系

四、自行车模型的运动学方程

自行车模型将车简化为前后两个轮子和一个轴，假设车轮轮距为0，

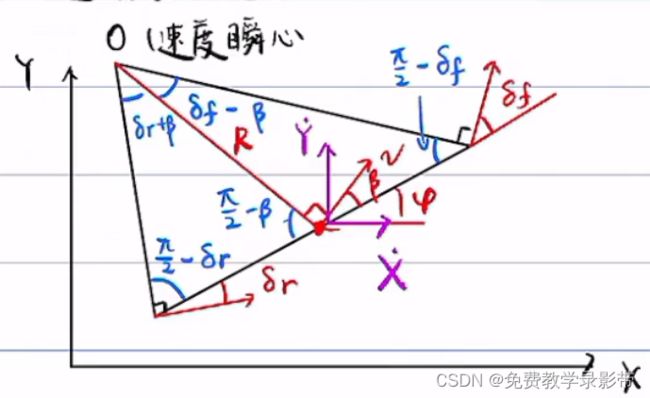
•  求质心速度：瞬心法

假设前轮速度v'，后轮速度为v，利用瞬心法求出质心速度vc

•  横摆角与航向角

 注意这里的前轮转角和后轮转角会由于轮胎的刚度而并不与方向盘转角一一对应，这里假设低速不考虑轮胎变形的自行车模型，所以前轮转角可以控制航向角

• 纵向车速与横向车速

 下面建立微分方程：即前轮转角如何影响到侧向位移与航向角

①根据几何关系建立运动学模型；②根据牛顿力学建立动力学模型

动力学模型更加复杂，考虑轮胎变形，参数很难准确。

运动学模型简单，所以只适用于低速转弯半径大的情况。

• 运动学模型

首先角度推导

利用速度投影得到几何关系：

此时并未体现前轮转角对于的影响，要进行进一步推导

设前轮到质心距离a，后轮到质心距离b，根据正弦定理

 展开后得到

 由于质心位置会变，所以a和b是变量，需要用一些不变的量来表示

使用（a+b）/R来表示，因为a+b=L为轴距不会变

这里由于质心侧偏角≈0，所以cosβ≈1

带入上面第三个式子，由此得到运动学方程：

 在低速条件下，认为车不会发生侧向滑动（漂移），vy≈0，这个时候质心侧偏角为0

一般后轮不转向，在低速条件下，认为=0，所以有下面这个运动学方程

 由于beta=0，所以横摆角约等于航向角

 其中为横摆角，v是质心速度

第三讲 轮胎侧偏与车辆动力学方程

运动学方程：简化过多，高速情况不适用

 动力学方程：考虑轮胎特性

一、动力学方程与Frenet坐标系解耦

当选取Frenet坐标系时，可以将纵向控制与横向控制解耦

纵向控制只需要管油门和刹车，不需要管方向盘，即与横向控制解耦

当纵向稳定时，横向控制只与方向盘转角有关

而运动学方程无法解耦，这就是为什么要使用动力学方程的原因

动力学+Frenet坐标系可以解耦

纵向位移s，s两阶导数是油门刹车决定的纵向加速度

横向位移d与方向盘转角的关系，这个关系汽车理论中给了，但是是在车身坐标系下面，所以如何把这个公式转换到Frenet坐标系是关键

下面的横向位移都用y来表示

二、轮胎的侧偏特性

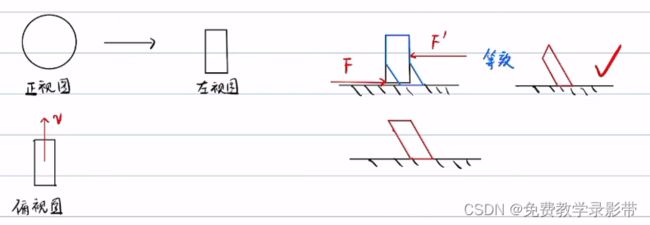
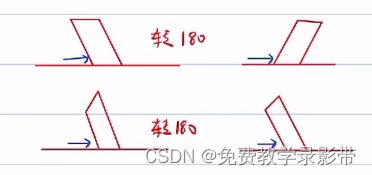
车辆轮胎受力后会变成圆台一样的形状，只能走圆弧，

为什么轮胎变形是一个梯形呢，因为梯形绕轮胎转轴转180还是原来的样子，而平行四边形不是了

侧偏会导致轮胎实际速度与期望速度方向有一个夹角，称之为侧偏角

侧偏角与受的侧向力呈正比

侧偏角定义：，其中C为侧偏刚度，侧偏刚度*侧偏角= 侧向力

注意：侧偏刚度一定为负数，负的侧偏力=>正的侧偏角

此外，侧向力一般用Fy来表示

三、考虑轮胎侧偏特性的自行车模型

二自由度模型可以在两个自由度的前提下，模型表示的比较准

注意都是负的，根据受力分析得到：（注意第一个公式是may，不是ay）

 假设比较小，有，把侧偏公式带入得到

验证：L为轴距，约等于3m；R为转弯半径，一般8-12m；

即

下面给出与y的关系以及的具体表达式

 与y的关系直接给出：

 注意这里后面还多了一项，因为这个公式是在车身坐标系下，要带上惯性力

加速度是个矢量，等于xy两个方向的速度乘单位矢量和，

 在直角坐标系下，单位矢量ex和ey是常矢量

在车身坐标系下，ex和ey不是常矢量，所以其导数不等于0，因此多出来了一项

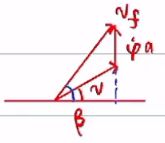
下面推导，

根据刚体的速度合成与分解，把vr移动到质心处，连接vr与v的线一定与车的轴线垂直，并且大小等于

下面放大看

 蓝色线的长度，竖着的蓝线为，进而推出

 为了保证是负数，一半phib比较大，vy比较小，所以可以交换一下位置，改变正负号

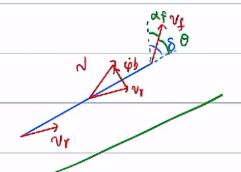
下面画出和，图中绿色角是，上面的角是

注意这里是前轮速度与车身x轴的夹角，是前轮转角。可以通过公式推出，这样就得到表达式。

我们把局部图放大来看，蓝色的角为上面绿色的角

对取tan得到，根据几何关系进而得到：，即，然后跟上面一样需要加一个负号保证\alpha_{f}为负数，就得到了下式

 得到带入上面公式得到（这里，下面公式写错）

 整理得到

 即可得到状态空间方程

第四讲 坐标变换与横向误差微分方程

要控制的目标就是：让汽车当前状态与规划的状态接近

规划给出：车位置（），速度、航向角、加速度 ，则可以计算出五个误差

定义：真实的-规划的 = 误差，得到误差的表达式 

控制目标是

 定义一个代价函数J= a*误差平方+b*u的平方，可以改写成向量形式

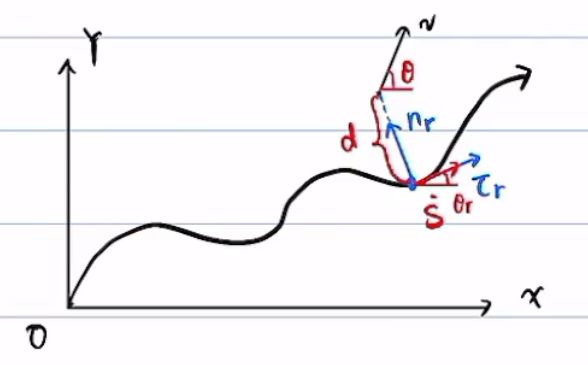
根据投影法定义5个误差，将速度v在自然坐标系下投影到规划的位置的切向与法向得到和d，投影在上面的速度为，车到投影的距离设为

 下面定义误差：横向误差自然为d，航向误差为，投影的速度大小为，速度误差为（这里是大小，不含方向，因为航向角控制了方向），速度误差属于纵向控制，暂时先不管

注意：这里的\tau和n和车身坐标系的x和y不是一个坐标系，因为v是质心速度，质心速度和绝对坐标系x轴的夹角为航向角\theta，而车身坐标系是以横摆角为方向，x轴是沿着横摆角的方向，y轴垂直横摆角方向，所以和n不是车身坐标系的x和y。（个人理解，两者差了一个质心侧偏角）

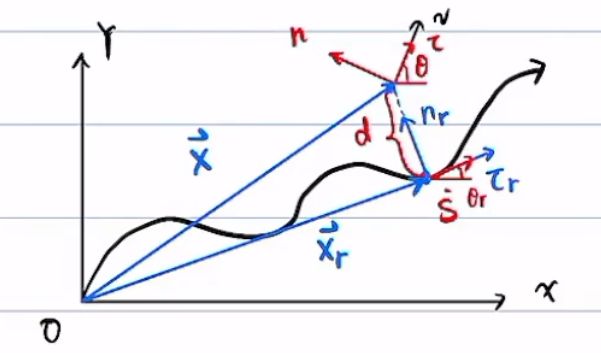
d为横向误差，和规划位矢xr与真实位矢x组成三角形，

根据矢量关系写出表达式，（这里d是一个数，不是向量，所以需要乘以方向向量nr）

算出d的表达式还不够，因为我们的状态空间方程式以为未知量，然而d和和没联系，为了联系起来，对d求导得

其中

这里注意nr并不是一个固定的常矢量，其方向会随着规划的位置而改变，和曲率有关

推导，假设矢量r经过dt时间到达r+dr，蓝色的为差值位矢dr，红色的弧线为ds

代入d的求导得到（注意这里前面的括号里， 和 垂直，所以点乘=0可以消掉）

最后一项，，这个没啥好说的，但是是啥呢？

这里就要用到Frenet公式求

带入得到

带入到上面公式得到，（ 和 垂直，所以点乘=0可以消掉后面一项）

 为了求和之间的夹角的关系，画出图，那么和之间的夹角可以通过几何关系得到

 带入后得到

接下来计算

对求导得到

再把上面推导的结果以及Frenet公式带入得到

 两边同时得到：

和之间的角度实际上就是

推导到这里，我们得到两个公式：

这两个公式非常重要，是一切工作的起点

还得把它与联系起来，带入航向角得到： 

注意上式中，自行车模型中vy喝vx都可以用v和质心侧偏角表示

d为纵向误差，令，（注意：其中不是航向误差，应该是，少了质心侧偏角，但是一般比较小，在可以忽略，但这个比较重要后面不能忽略）

求出vy和ephi的一阶二阶导数

一般道路平缓，所以忽略的二阶导数

 带入二自由度动力学方程，再化简得到ed两点（这里是由于要消掉vx和vy）

同理带入，得到\e_{\varphi}两点

 这两个方程就是误差的微分方程，下面进行简化 

凑成下列控制方程 ，由此得到误差线性微分方程

遗留的三个问题

（1）航向误差问题：缺少质心侧偏角

（2）如何计算方程中最后一项：

（3）去掉最后一项小尾巴可以用LQR计算，加上后怎么控制

第五讲 连续方程的离散化与离散LQR原理

先暂时忽略这一项，公式转换为

Matlab有现成的包：lqr(A,b,Q,R)和dlqr(A,B,Q,R) (离散化LQR)可以算出u

主要应用为dlqr，连续lqr很难

dlqr原理只涉及到拉格朗日乘子法

拉格朗日乘子法：求f(x,y)在约束g(x,y)=0条件下的极值：

dlqr问题：

 求

 这个极小值一定是最小值

所以将dlqr问题分解成俩问题

一个是如何离散化 ，另一个是如何求解优化问题

一、离散化模型

离散化：可以使用向前欧拉法或者中点欧拉法，apollo是两者的混合

先积分消掉x·，再使用中值定理进行近似

向前欧拉法、向后和中点欧拉法则是如何替代 

可以将x(t+dt)用x(t)表示出来

对于我们这个问题就可以先积分再用中值定理

然后再将和代替，这里使用向前欧拉，因为u(t+dt)不知道

 化简得到

dt为采样周期，完成离散化

 二、求解lqr

下面推导ldqr的解法

先让J从0计算到n，然后再让n趋于无穷。这里拆分成0到n-1和第n项。(这一步我的理解是，因为要推导出第n和n-1步之间的递推关系，所以要这么分解)

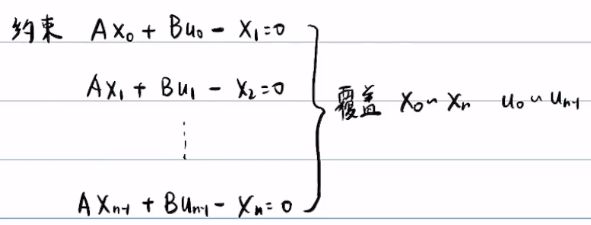
 写出约束

 约束刚好完全覆盖自变量，如果把第n个约束添加进去，会多加一项x_{n+1}

如果n趋于无穷，有没有n+1这项无所谓

所以可以使用拉格朗日乘子法，把J写成

 下面对其化简

下面要对J进行求导，所以先给出向量导数的定义 ：

这里的 

分别对自变量求导得到

再把刚才化简得Hk求偏导带入上面的式子中

得到以下式子（注意这里笔误：这里③式k是从0开始），一共是3n-2个式子

 下面基于上式求出递推式

 将⑧与④进行对比

为了求出与的关系

得到Pn=Q以及Pk-1的表达式：

  基于这两个式子，可以以Pn=Q为初始值，一直从k=n推导到k=0

 也就是说我们知道了与的关系，下面再关注②式，可以将由表示出来

式子中的R，B，A均为已知量，P是黎卡缇方程算出来的

注意这里的xk，一般可以用误差来表示，根据上面对状态空间方程的定义有xk=err

err可以通过定位和规划得到

所以uk可以由已知量算出

此外注意，这里的输入uk是车的前轮转角，只有一个数，因此B是一个4*1的向量

三、黎卡缇方程

注意：对于黎卡缇方程，如果n区域无穷大，那么黎卡缇方程要迭代无数次，但是实际情况是Pk迭代几十次后就会收敛，即从Pk一直到P0均相等，这个性质非常好，可以帮助我们处理无穷时间

所以

解黎卡缇方程的步骤为先给P取初值，然后迭代求出P，然后再根据P求出u

课本上面的黎卡缇方程为

和我们这里其实一样，只是方程形式写的不一样，推导一下

 我们上面推导的黎卡缇方程为4*4矩阵求逆，课本给出的这个是1*1求逆，即求倒数。

矩阵求逆是基于数值的方法，所以1*1求逆精度会更高，所以推荐使用下面这种。

四、总结

第六讲 前馈控制与航向误差

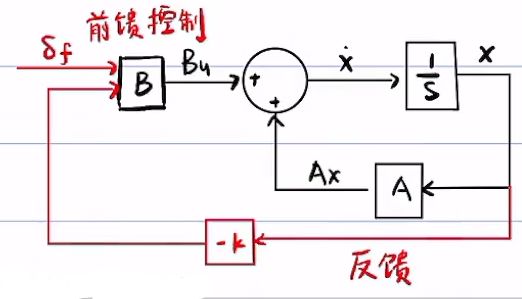
的框图表示

如果u = -kx，即相当于加上一个反馈，如图所示

 容易出现代数环问题，输入影响输出，输出影响输入，这里先不管，后面可以用matlab加延时的方法解决

一、前馈控制

在上面的框图内再加一个输入量，变成前馈控制 

因为我们要解决第四讲的遗留问题，即如何处理这个小尾巴

如果只用LQR，

无论k取何值，和不可能同时为0，即不可能永远为0，因为，不是该微分方程的解

所以要引入前馈控制：，其中-kx是由LQR计算出的反馈控制，为前馈控制

前馈控制的引入是为了消除稳态误差

LQR最终会导致，，此时的稳态误差可以计算得到：

引入前馈控制后，有 

稳定后的

目的：选取合适的，使得尽可能为零

上面已经推导出了A，B，C，注意这里的

 把ABC带入，用软件Mathmatica计算得到err的表达式

可以看出每项都有这一项，此外注意

对的影响

 先算反馈K，再算前馈

无论前馈反馈取何值，

下面对进行化简，首先利用几何关系求出

 求曲率

利用曲率k求出与s的关系，这边做了很多假设

 带入后得到与vx的关系

 然后求出ay和vx的关系，

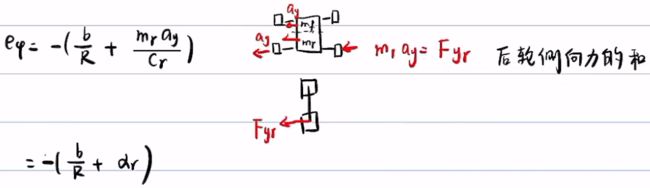
再带入上式把vx2消掉，得到

其中，may为总侧向力，cr为后轮侧偏刚度

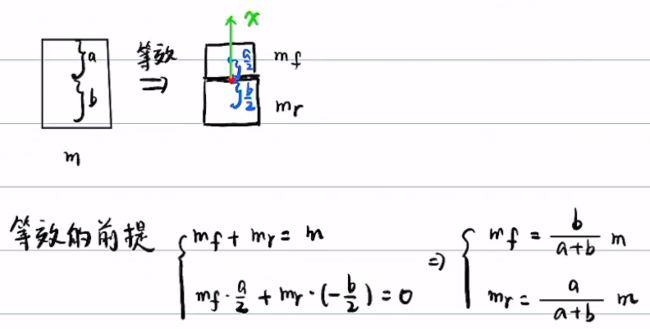
将车辆等效成前后两部分，分别计算出前后质量

根据后轮侧向力与ay的关系，以及等效关系，将其进一步化简

 根据几何关系

 得到的刚好等于，

  虽然不是航向误差，但是其稳态误差为

虽然不可能通过，K去调节，但是我们不用理会。

因为最终目的是，即，而的稳态误差恰好为，所以不用管。

 至此，得到u的表达式

 其中K是通过lqr计算得到，通过前馈控制得到

第七讲 离散规划轨迹的误差计算

基于前六讲已经算出u的表达式

误差的计算在第四讲

其中：

 只要知道

 就可以把误差计算出来

 若规划的曲线是连续的，可能会导致投影不唯一

若A与A'的连线与A'的切线垂直，则A'为A的投影 

若曲线是连续的，不仅仅是投影麻烦，而且要处理多值问题，因此要离散

一、离散的轨迹点的误差计算

将轨迹离散成一些点，每个点都有四个信息

如何计算基于离散的误差呢？

方法如下：

①找到离散轨迹规划点中与真实位置（x,y）最近的点

 这个点在Apollo里面称之为match-point（匹配点）

②匹配点代替投影点的前提：规划的点很密

 现实情况是规划不能很密，否则计算量过大，所以需要通过匹配点近似算出投影点

 假设：从匹配到投影点的曲率k不变。即认为匹配点和投影点的轨迹近似用圆弧代替

匹配点的切向向量和法向向量

匹配点与车实际点的向量：

 ③求出ed（有正负：左为正，右为负）

 ④求出es：匹配点与投影点的弧长（es有正负）

 正代表投影在匹配点前面，负代表在匹配点后面

 ⑤（apollo）

⑥算出误差

 这样就可以算出离散的err，再使用离散LQR计算出K，进而计算出

第八讲

一、横向控制算法与流程图

（1）算法输入输出过程

首先要搞明白算法，才能写代码

 注意这里第四步为：，不是x

（2）流程图

 （3）具体算法

 ①A，B计算模块

up勘误:这里矩阵第四行第二列第三列写错了,第五讲开头那个矩阵才是对的

注意要考虑当= 0时的奇异性 

②LQR模块

因为A，B只与整车参数和有关，整车参数近似认为不变

情况1：如果加速度非常大，惯性力就比较大，这个时候前轮垂向力减少很多，后轮加大，侧偏刚度改变。此时仍然可以使用自行车模型，只是侧偏刚度改变。

情况2：急速过弯时，左右轮不对称，导致自行车模型不适用，所以在路径规划的时候要极力避免急速过弯的情况

A，B只与整车参数和有关，或者 

每个都有唯一的一个K与之对应

所以可以离线算出与K的对应表，实际应用中不需求解Riccati方程，直接查表

优点：速度大大加快

缺点：耗费储存空间（空间换时间） 

个人理解：针对每个vx，可以求出对应的AB，对于每个AB都可以迭代算出P，然后算出对应的K

MATLAB自带的模块，只需要输入A，B，Q，R即可得到K

③计算模块

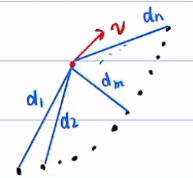
首先要有离散的规划点

遍历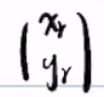找到距离当前车的位置最近的规划点，该点的序列（index）记为dmin

写出匹配点的切向向量与法向向量

写出误差距离向量(个人理解：这里的x_dmin就是上面的xm，即投影点的坐标，d_err为匹配点与车实际位置之间的位矢)

 算出误差ed和es（个人理解：ed是投影点和实际位置之间的位矢，es是投影点与匹配点之间的位矢）

算出（个人理解：这里的是匹配点的曲率）

 算出其他误差和变量

 输出

④前馈控制计算模块

⑤最终控制计算模块

 （4）预测模块

车有惯性，所以要提前控制，要增加一个预测模块

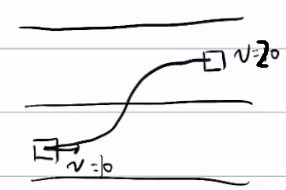
举例：如下图，假设当前位置不在路径上面，但是速度朝向路径，如果是人在开车，他不会打方向盘改变方向，但是算法为了减小误差，它会打方向盘为了减少误差

这个例子也是一样，如果当前点在路径上，算法不会打方向盘，但是人知道要转弯

算法控制具有滞后性，所以要加上预测模块，让算法有预见性

解决办法：使用预测点代替真实点去计算误差

 预测算法写法：

首先有个预测时间，记为ts，可以使用速度×时间得到位置

 根据运动计算出预测点的全部信息

至此介绍完毕算法流程图，下面搭建仿真平台

二、CarSim与Matlab联合仿真基础

CarSim这里使用2019版本，具体下载和安装可参考下面这个视频

最新！Carsim2019详细安装教程【附安装包】_哔哩哔哩_bilibili

 （1）CarSim于Simulink基础设置

首先要知道两个重要路径

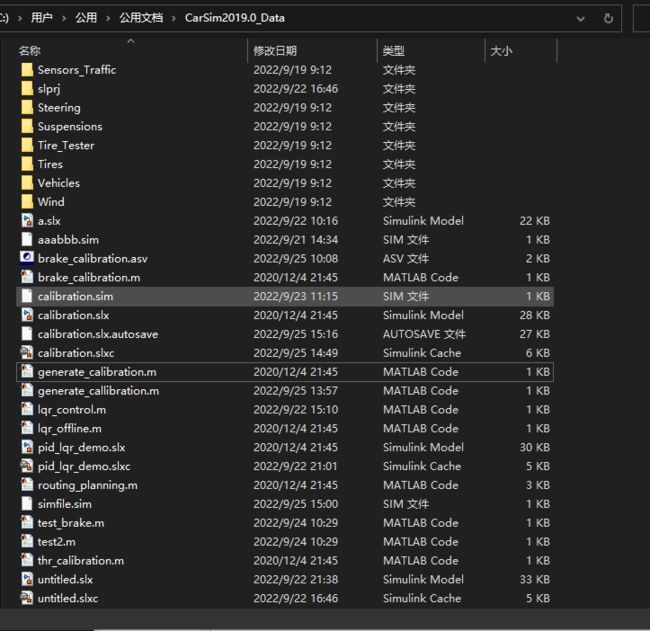
CarSim默认数据库路径：C:\Users\Public\Documents\CarSim2019.0_Data

CarSim安装路径：E:\CarSim2019.0_Prog

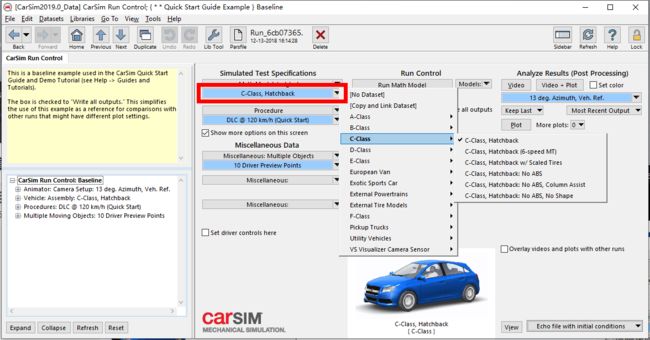
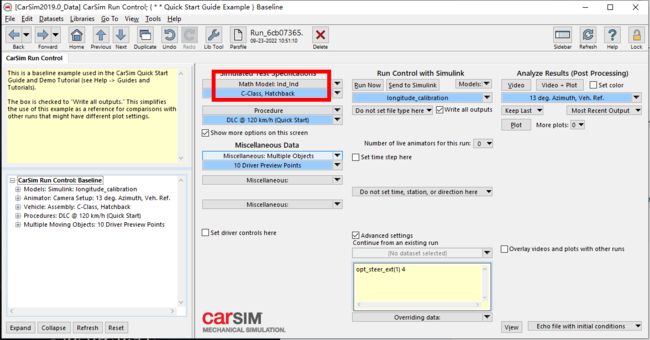
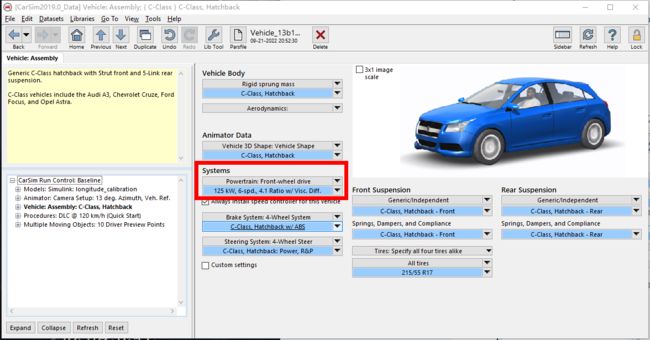
打开CarSim软件，需要选择数据库路径

 点击continue进入

注意这个时候是灰色的不可选的状态，点击Lock就可以解锁，进行选择

 点击这里选择车辆，ABCDE级车，每个车的惯量，尺寸等参数都不一样

整车尺寸参数

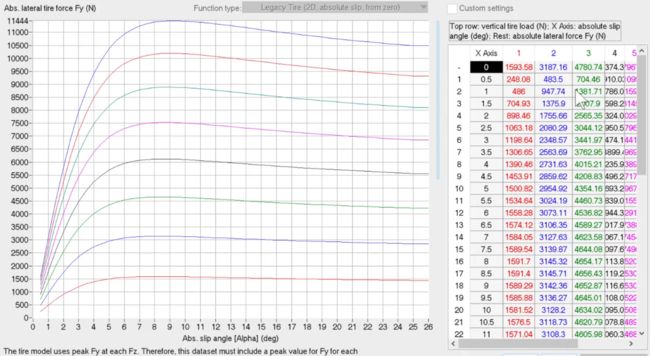
进入轮胎界面，可以看到Fy：侧偏曲线：侧向力与侧偏角的关系曲线，

由于做控制，不允许大侧偏角，容易失稳，只考虑小侧偏角下的曲线，此时斜率为侧偏刚度

 model选择Simulink

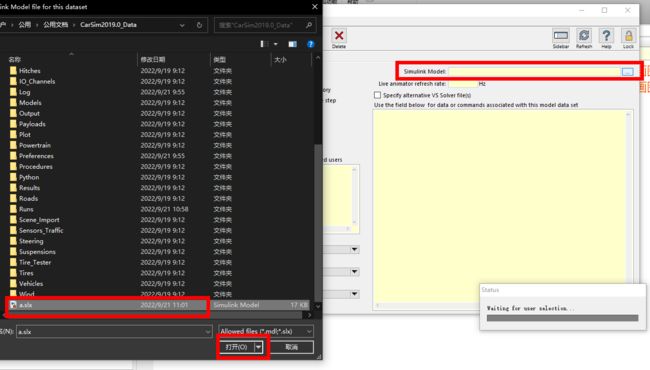
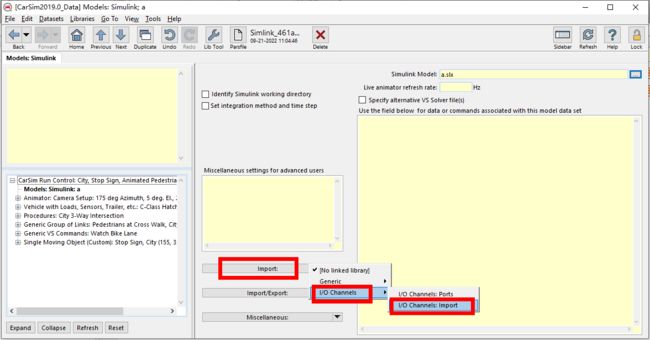
 点击这个地方，新建一个数据库

新建数据库，起名叫a

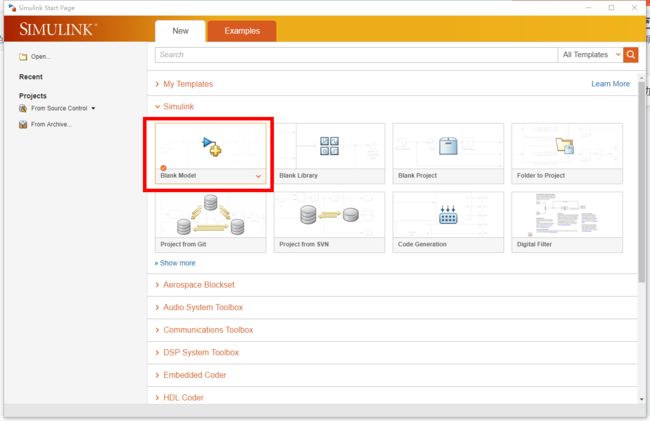
 然后需要填入simulink模型，这里没有，所以新建一个，打开Matlab

 打开MATLAB，选择Simulink

 创建好空模型，然后直接Save as，保存到数据库路径，设置文件名为a，这里可以和CarSim的不一样

 将刚才两个重要路径都添加进MATLAB路径

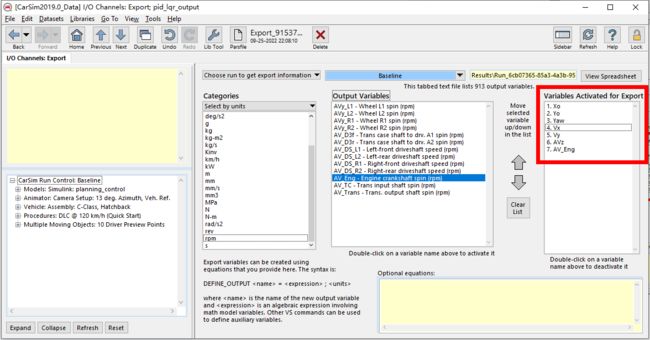
 （2）输入输出设置

设置输入

 新建数据库并起名字ain‘

同样把输出aout也新建好

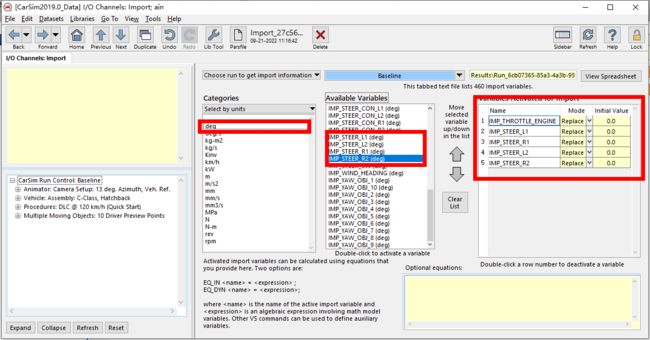
 点击ain，进入设置，选择Baseline

选择Select by units

将油门，前轮后轮转角都加入，完成设置

注意：L1是左前，L2是左后，R1是右前，R2是右后

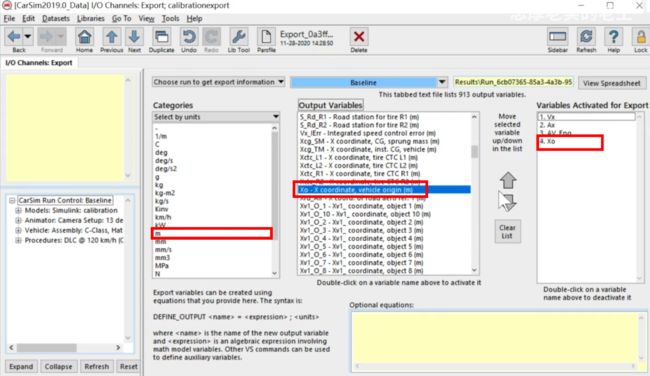
 同理设置输出，为如下几个变量

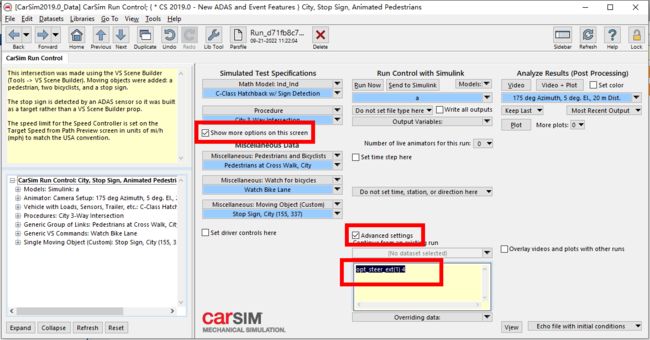
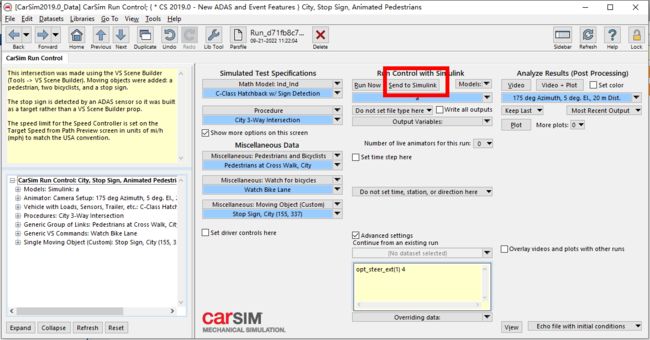
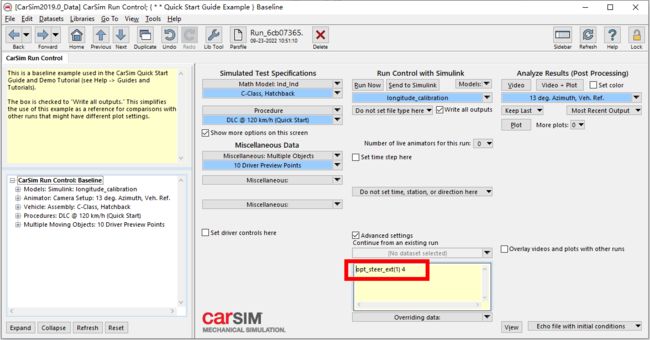
 接下来回到主界面，然后选择SHow，Adcanced，再加上这句话： opt_steer_ext(1) 4

因为目前只能通过方向盘转角来控制，而我们是通过前轮转角控制，加上之后就是前轮转角控制

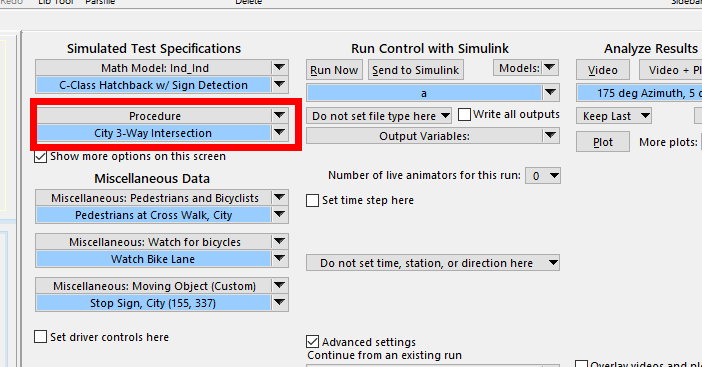
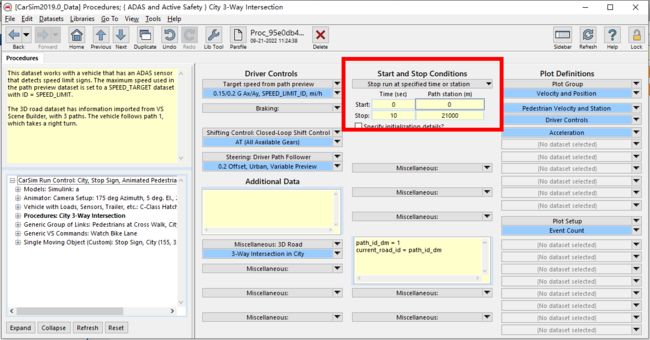
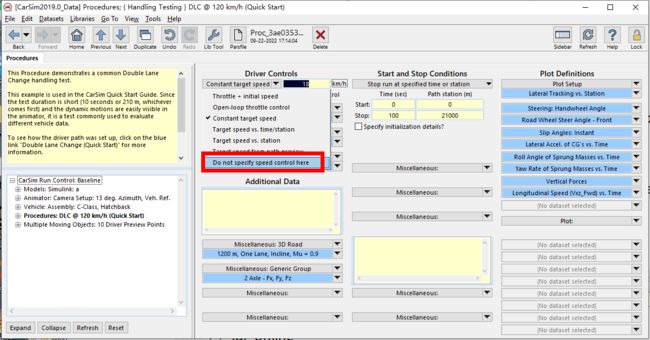
  Procedure里面可以设置仿真时长和距离

这里设置为10s和21000m

 一切准备就绪，点击Send to simulink

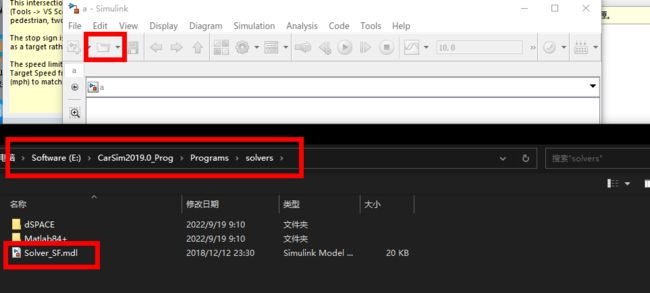
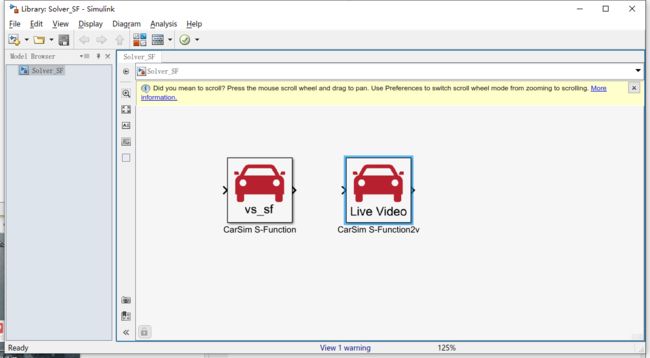
打开Simulink后，有两种方法导入SF函数，方法1是和老王一样，这种在2016可以用，点击选择文件，进入安装路径，选择Solver_SF.mdl打开

方法2是CarSim2019可以直接在libray拉进来

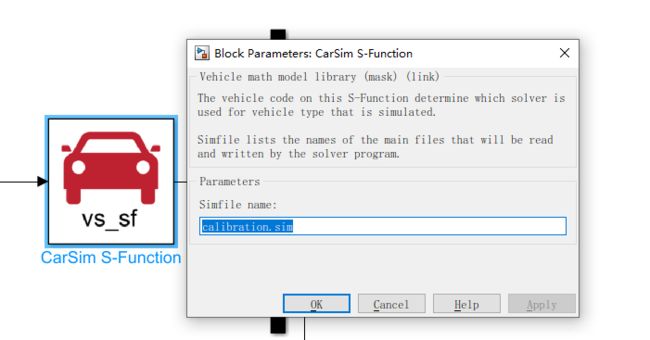
不管是那种方法，都需要把SF函数这个里面填入名字和数据库路径下的sim文件名字相同

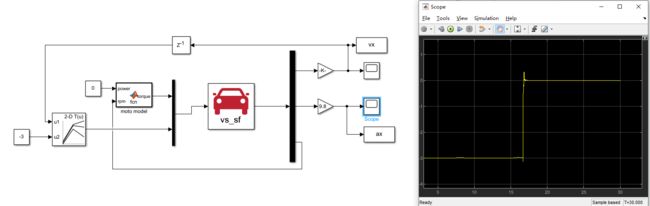
然后加一个5输入mux，，分别是输入油门设这位0.5，前后轮转角设置为0。后面再加一个demux，前两个接给示波器看下位置变化

点击仿真Run

再点击示波器

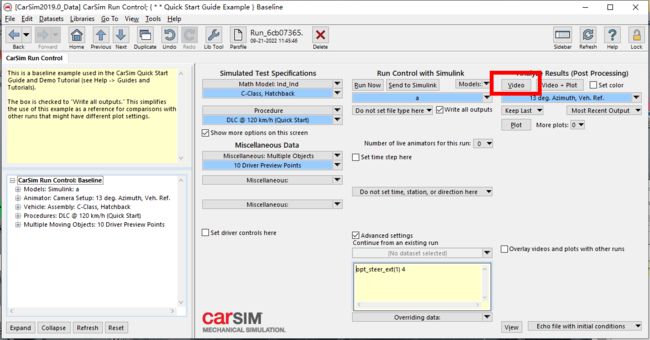
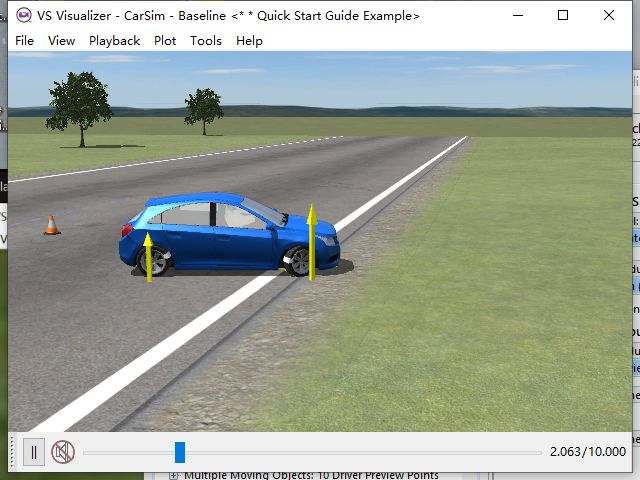
 回到CarSim，点击Video就可以看到仿真视频

其结果应该是走一条直线（因为并未给前后轮转角），共花费10s

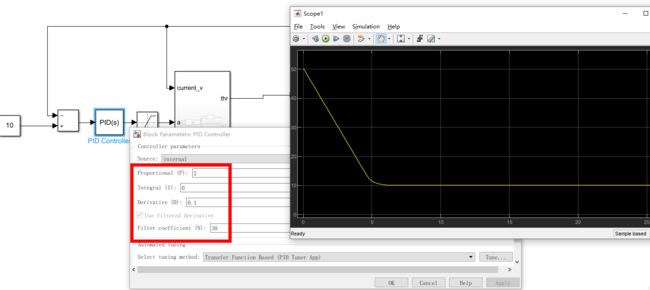
 Simulink将前轮转角改成30，看仿真结果

结果为原地画圆

三、代码与模型

代码下载地址：老王github上VincentWong3/automated-driving-control (github.com)

嫌麻烦的话可以在这里下载

automated-driving-control-main.zip - 蓝奏云

在写代码之前，先要明确算法流程

我们需要的是整车参数，车辆状态以及规划

整车参数可以在CarSim里面

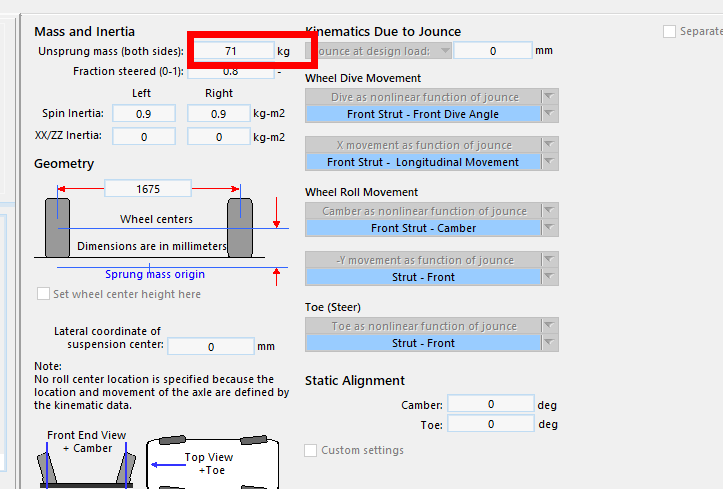
 注意这里的质量1270是簧上质量，还需要加上悬架质量71，总质量是1412

 此外需要注意的是侧偏刚度的单位，以及加上负号，由于是自行车模型还要乘以2

 把空气动力学关掉，暂时忽略风阻的影响

 由于需要用到车辆状态，所以需要在CarSim中输出状态

（1）路径规划信息生成

由于需要规划的路径，所以这里需要一个规划函数给出信息，这里对应的是routing_planning.m文件，里面有两个函数，一个是直线，一个是圆弧

straight函数：输入起点和终点坐标以及初始角和离散点数量，生成这样一系列点

function[xr,yr,thetar,kr]=straight(init_coord,end_coord,init_angle,count)
delta_x=(end_coord(1)-init_coord(1))/(count-1);
delta_y=(end_coord(2)-init_coord(2))/(count-1);
for i=1:count
    xr(i)=init_coord(1)+delta_x*i;
    yr(i)=init_coord(2)+delta_y*i;
    thetar(i)=init_angle;
    kr(i)=0;
end      
end

用法举例：

[xr,yr,~,kr]=straight([0,0],[50,50],pi/4,10);
scatter(xr,yr)

 arc函数：输入起点终点坐标以及起点终点角度以及点的数量

function[xr,yr,thetar,kr]=arc(init_coord,end_coord,init_angle,end_angle,count)
    L=sqrt((init_coord(1)-end_coord(1))^2+(init_coord(2)-end_coord(2))^2);
    R=L/sqrt(2*(1-cos(end_angle-init_angle)));
    delta_angle=(end_angle-init_angle)/(count-1) ;
  
       for i=1:count
           if delta_angle>0
               xr(i)=init_coord(1)-R*sin(init_angle)+R*sin(init_angle+delta_angle*(i-1));
               yr(i)=init_coord(2)+R*cos(init_angle)-R*cos(init_angle+delta_angle*(i-1));
               thetar(i)=init_angle+delta_angle*i;
               kr(i)=1/R;
           else
               xr(i)=init_coord(1)+R*sin(init_angle)-R*sin(init_angle+delta_angle*(i-1));

               yr(i)=init_coord(2)-R*cos(init_angle)+R*cos(init_angle+delta_angle*(i-1));
               thetar(i)=init_angle+delta_angle*i;
               kr(i)=-1/R;
           end               
       end  
end

用法举例：

[xr,yr,~,kr]=arc([0,0],[50,50],0,pi/2,100);
scatter(xr,yr)

 根据这两个函数，可以设计出一条路径出来，并包含每个离散点的xr,yr,thetar以及kr

count=50;
[x1,y1,theta1,kr1]=straight([0,0],[20,0],0,count);
[x2,y2,theta2,kr2]=arc([20,0],[30,10],0,pi/2,count);
[x3,y3,theta3,kr3]=arc([30,10],[40,20],pi/2,0,count);
[x4,y4,theta4,kr4]=arc([40,20],[40,40],0,pi,count);
[x5,y5,theta5,kr5]=arc([40,40],[35,35],pi,3*pi/2,count);
[x6,y6,theta6,kr6]=arc([35,35],[25,35],3*pi/2,pi/2,count);
[x7,y7,theta7,kr7]=arc([25,35],[15,35],pi/2,3*pi/2,count);
[x8,y8,theta8,kr8]=arc([15,35],[5,35],3*pi/2,pi/2,count);
[x9,y9,theta9,kr9]=arc([5,35],[-15,35],pi/2,3*pi/2,count);
[x10,y10,theta10,kr10]=straight([-15,35],[-15,15],3*pi/2,count);
[x11,y11,theta11,kr11]=arc([-15,15],[0,0],3*pi/2,2*pi,count);
xr=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11];
yr=[y1,y2,y3,y4,y5,y6,y7,y8,y9,y10,y11];
thetar=[theta1,theta2,theta3,theta4,theta5,theta6,theta7,theta8,theta9,theta10,theta11];
kappar=[kr1,kr2,kr3,kr4,kr5,kr6,kr7,kr8,kr9,kr10,kr11];

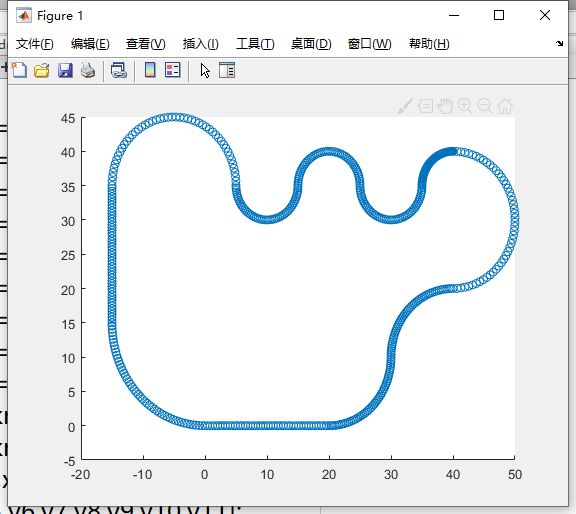
scatter(xr,yr)

这里使用的路径并不是好路径，会发生曲率突变，只是用作演示用直线和圆弧简单拼接

回到CarSim设置路面

进入Procedure

 选择Two Lanes

 进入道路设置

设置和刚才规划一样的道路，先解锁，然后Rows改成11，然后照这样填表，

此外把Treat as loop也点上

接下来点击Video查看建造的道路结果，注意一定要改成Flat

这个道路转弯半径非常小，最小只有5m，路径非常严苛，可以查看我们的控制效果

接下来回到MATLAB（注意这里还是跟只前一样，最好send to simulink），先运行一下，让变量在工作区内

接下来打开simulink，pid_lqr_demo里面已经写好了，这里重写一遍

（2）预测模块代码

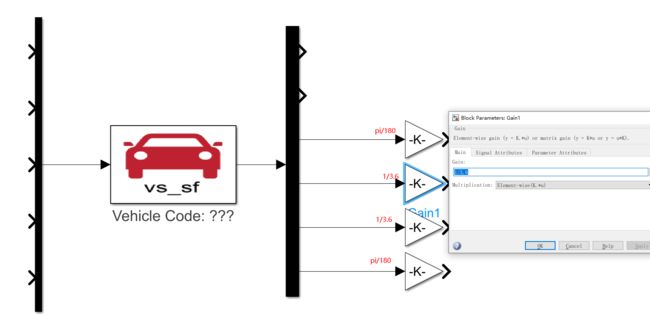
首先5输入6输出，然后单位换算，

 新建matlab 函数，预测模块比较好写，先写预测模块，把每个输出标出来

预测模块的算法

输入为当前状态和速度v，预测时间ts

输出为预测的状态，算法为

代码如下：

function [pre_x,pre_y,pre_phi,pre_vx,pre_vy,pre_phi_dot] = fcn(x,y,phi,vx,vy,phi_dot,ts)
pre_x = x + vx*ts*cos(phi) - vy*ts*sin(phi);
pre_y = y + vy*ts*cos(phi) - vx*ts*sin(phi);
pre_phi = phi+phi_dot*ts;
pre_vx = vx;
pre_vy = vy;
pre_phi_dot = phi_dot;
end

simulink里面还要输入单位换算，ts设置为0.1

（3）误差计算模块代码

根据流程图，下一步是误差计算模块

输入的为预测点信息，规划的信息。输出为投影点的曲率和误差。

算法流程如下：

 代码

function [kr,err] = fcn(x,y,phi,vx,vy,phi_dot,xr,yr,thetar,kappar)
%找到规划轨迹的长度，即多少个规划点，最短距离d_min，序号记为min
n = length(xr);
d_min = (x - xr(1))^2 + (y - yr(1))^2;
min = 1;
for i = 1:n
    d = (x- xr(i))^2 + (y - yr(i))^2;
    if d < d_min
        d_min = d;
        min = i;
    end
end
%找到最短点序号，按照算法一步一步来
dmin = min;
tor = [cos(thetar(dmin)); sin(thetar(dmin))];
nor = [-sin(thetar(dmin)); cos(thetar(dmin))];
d_err = [x - xr(dmin); y - yr(dmin)];
ed = nor' * d_err;
es = tor' * d_err;
% 算thetar两种方法
projection_point_thetar = thetar(dmin); %apollo
% projection_point_thetar = thetar(dmin) + kappar(dmin) *es;
ed_dot = vy * cos(phi - projection_point_thetar) + vx * sin(phi - projection_point_thetar);
%%%%%%
%第九步这里加个sin，假设较小用正弦代替，消除±2pi的印象
ephi = sin(phi - projection_point_thetar) ;
s_dot = vx*cos(phi - projection_point_thetar) - vy * sin(phi - projection_point_thetar);
s_dot = s_dot/(1 - kappar(dmin) * ed);
ephi_dot = phi_dot - kappar(dmin) * s_dot;
kr = kappar(dmin);
err = [ed;ed_dot;ephi;ephi_dot];
end

其中xr，yr，thetar，kappar用from workspace模块导入（运行simulink的时候必须提前工作空间内有，如果避免麻烦都弄成行向量）

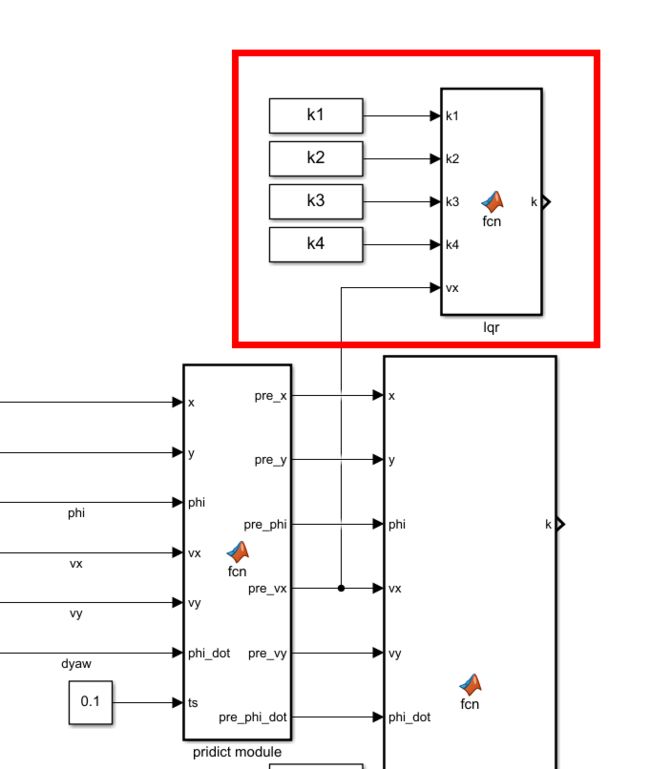
（4）LQR模块代码

下面写LQR模块，matlab有自带的lqr包，可以直接使用

首先定义好参数，然后使用matlab自带的lqr包算出来K，然后拆成k1,k2,k3,k4

cf  = -110000;
cr = cf;         %差别不大，近似认为是一样的
m = 1412;   %质量，包含簧上质量和悬架质量
Iz = 1536.7;  
a = 1.015;
b = 2.910 - 1.015;
k = zeros(5000,4); %LQR 的K矩阵
for i = 1:5000
      vx = 0.01*i; %每隔0.01秒刷新一下K，0-50m/s
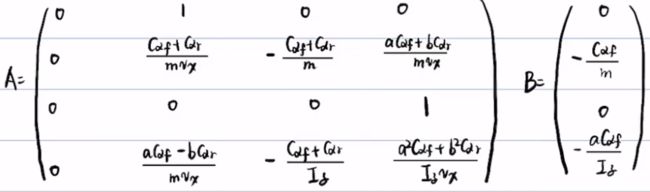
      A = [0,1,0,0;
          0,(cf+cr)/(m*vx),-(cf+cr)/m,(a*cf-b*cr)/(m*vx);
          0,0,0,1;
          0,(a*cf-b*cr)/(Iz*vx),-(a*cf-b*cr)/Iz,(a*a*cf+b*b*cr)/(Iz*vx)];
      B = [0;
          -cf/m;
          0;
          -a*cf/Iz];
      Q= eye(4);
      R = 100;
      k(i,:) = lqr(A,B,Q,R); %k就是离线lqr的表
end
%由于Simulink没法传矩阵，只能传行向量  
k1 = k(:,1)';
k2 = k(:,2)';
k3 = k(:,3)';
k4 = k(:,4)';

simulink新建一个lqr函数，根据vx来选择对应的k

function k  = fcn(k1,k2,k3,k4,vx)
if abs(vx) < 0.01
    k = [0,0,0,0];
else
    index = round(vx/0.01);
    k = [k1(index),k2(index),k3(index),k4(index)];
end

end

运行一下获取四个k，然后输入进lqr

 （5）前馈控制模块代码

接下来是算前馈的模块，需要整车参数，vx，kr（投影点的曲率），直接带公式

 代码

function forward_angle = fcn(a,b,m,vx,cf,k,kr)
forward_angle = kr*(a+b-b*k(3)-(m*vx*vx/(a+b))*(b/cf)+(a/cr)*k(3)-(a/cr));
end

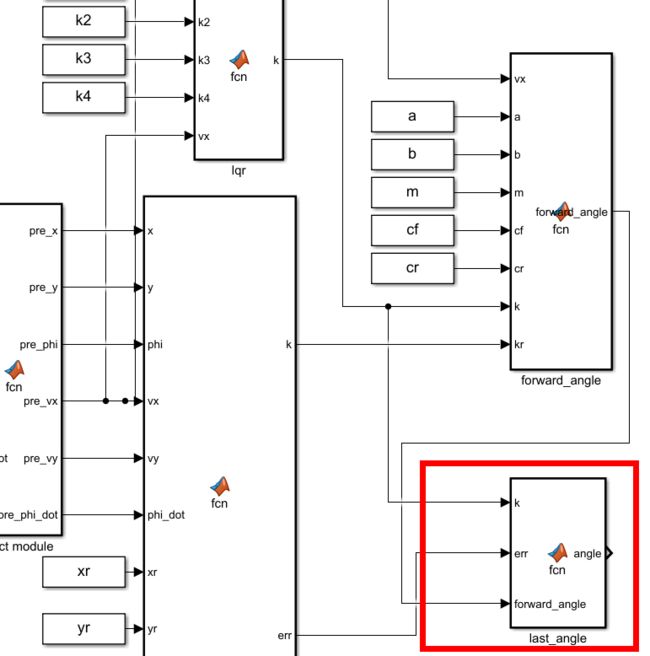
（6）整合模块代码

最后一个整合模块

function angle = fcn(k,err,forward_angle)
angle = -k * err + forward_angle;
end

 （7）仿真运行

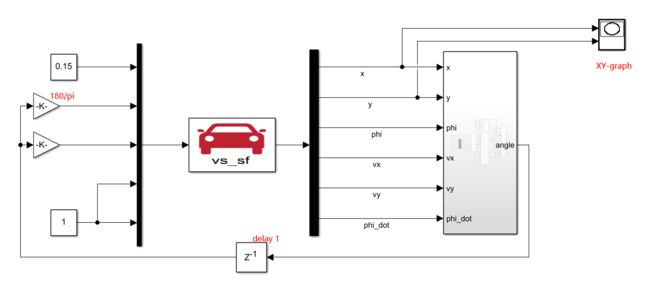
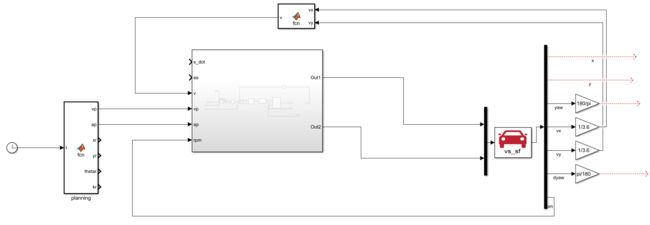
此时所有代码写完了，打包封装一下，选中SF输出的模块 Crtl+G打包

将输出的angle反馈给CarSim，注意弧度转换为角度，CarSim是角度

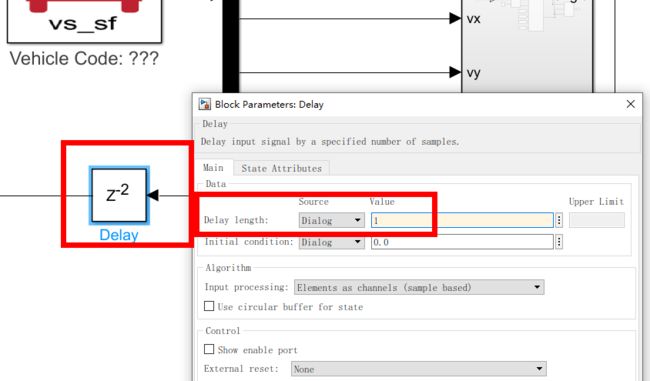
再加一个延迟模块，作用是：如果输入是这一时刻的值，输出是上一时刻的值。等于延迟一个单元，为了避免代数环。

节气门开度给个0.15，后轮转角给个0

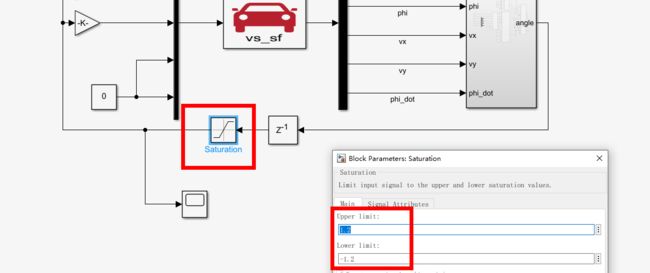
此外给angle加一个限制防止角度太大超过物理限制，再加一个示波器查看angle变化

此外，将初速度调成不设置初速度（默认120），因为速度过大，道路严苛，很难控制容易报错

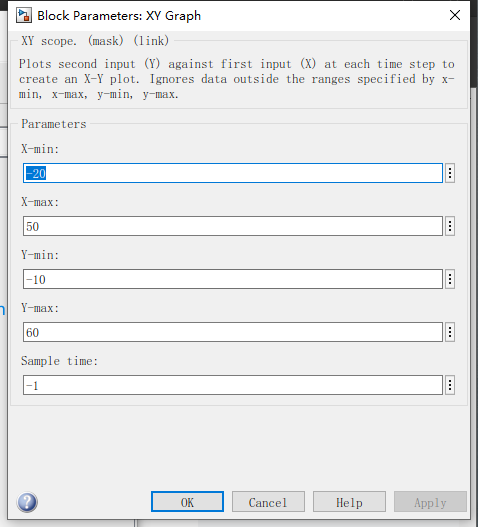
点击run，使用XY-graph查看

 X范围有点小，调大

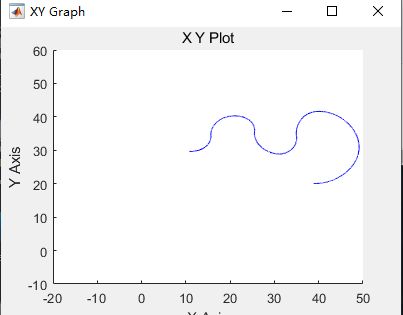
这个时候点击run

仿真结果如图所示（注意如果时长短是因为上面Procedure里面改成10s仿真了，只需要改成50S然后再Send to Simulink即可）

回到CarSim点击Video查看实际运行视频

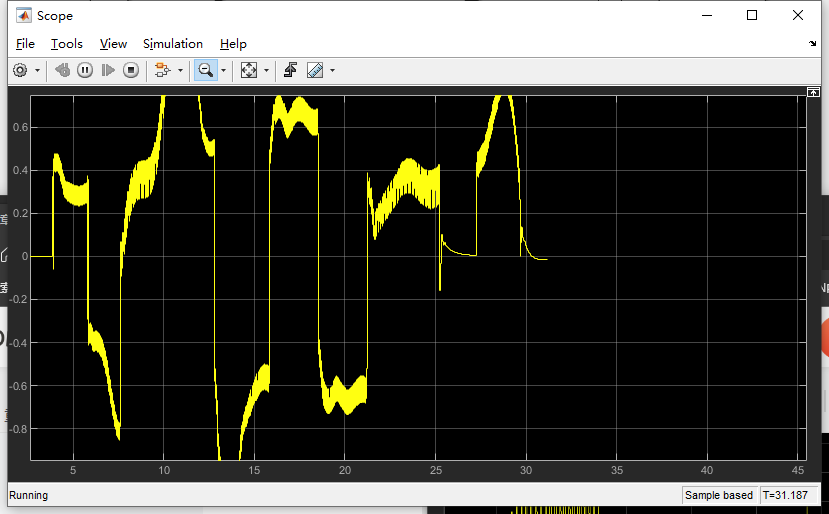
前轮转角不停抖来都去

 改进方法

计算thetar的时候，加上es，这样就可以防止大抖动，减少抖动

但是这种方法没法解决突变问题，因为规划的曲率突变，控制很难解决，得在规划的时候进行插值让曲率连续，要不然就把ＬＱＲ的Ｒ调大一点

另外，不能让规划的点过少，这样会让车围绕一个点不停打转，因为匹配点不会改变

第九讲  纵向控制开篇

纵向控制比较简单，不需要太多的数学知识

一、纵向控制逻辑

首先要明白：当你踩下油门/刹车时，你到底在控制什么？

横向控制逻辑：方向盘-->前轮转角-->车的航向角

纵向控制：油门/刹车--> ？--> 车加速/减速

这里的？到底是什么，到底什么被改变了，导致车速改变

直观上想到发动机转速或者发动机扭矩

正确答案：油门-->发动机功率被改变-->?-->车加速

刹车-->制动压力增大-->制动盘摩擦增大-->阻力增大-->车减速

功率与车加速不直观

什么与车加速直接相关？车速加大，只需要加速度大于0即可，车速与发动机转速相关，而加速度与发动机扭矩相关

纵向控制逻辑：油门 --> 功率 --> 转速 / 扭矩 --> 车速 / 车加速度 --> 车加速

当踩油门时，到底在控制什么？

P与M，ω之间的关系：   

真实的发动机扭矩转速功率之间的关系需要用实验曲线来获得

二、发动机与变速器

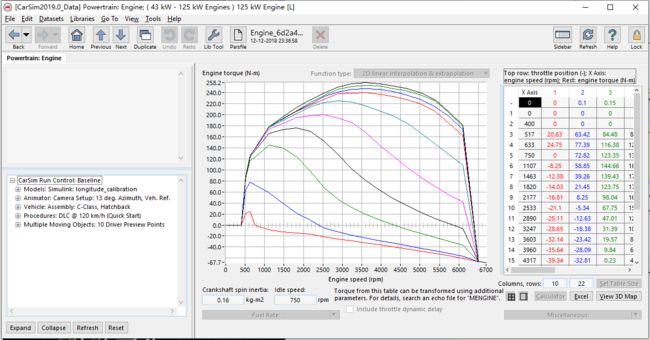
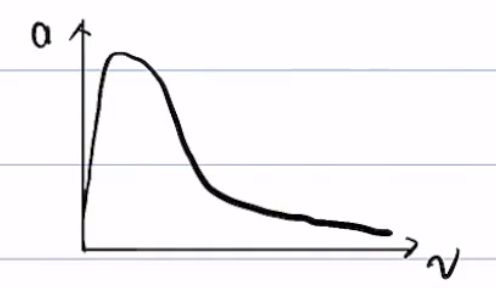
发动机扭矩-转速曲线

并不呈反比例曲线，因为P一部分用于发热，低速情况热占主导，高速情况做功占主导。

所以发动机最好只在高效/高扭矩区运行，发挥其最大优势，但是其高效区很短

变速器应运而生， 把发动机转速降低

 变速器通过齿轮切换从而将发动机的高效转速得以拓宽

 齿轮切换术语叫换挡：一档二档三档四档五档

一档最慢，扭矩最大，用于启动爬坡

五档最快，扭矩最小，用于高速

发动机与电机的转速扭矩图

电机在前面就有很大扭矩，最高转速16000，高效区间长，效率最高90%

发动机在前面运行，最高转速6500，高效区间很短，效率最高40%

因此发动机一定需要变速器，电机不一定需要变速器

发动机低速差，高速较强。电机在低速加速极强，高速差。

我们的控制基于电动汽车，电动车控制简单且为大势所趋，不需要考虑换挡策略

电机工作区间分为恒扭矩区和恒功率区，在到达最大转速前扭矩不变，到达之后功率不变

三、CarSim基础设置

由于CarSim没有电机，所以需要造个电机，下面为假设

电机参数：最大扭矩380Nm，最大功率180kW

 估算出其最大转速

 M与ω之间的关系为

 虽然是假设的电机，但是方法是通用的，不管电机参数如何，都通用。

我们的方法是通过实验标定来的，哪怕曲线乱七八糟的也有效果

下面进入CarSim设置电机

先新建一个模型

 设置输入为发动机扭矩

 输出为Vx，Ax以及曲轴的转速

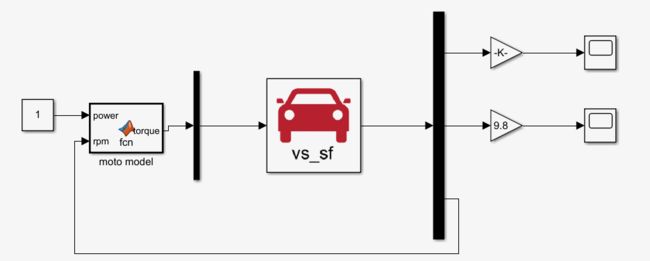
 接下来send to simulink

设置电机模型

function torque = fcn(power,rpm)
Tmax = 380*power;
if(rpm <= 4523)
    torque = Tmax;
else
    torque = Tmax * 4523/rpm;
end
end

接下来进入CarSim的C-class

 进入变速器设置

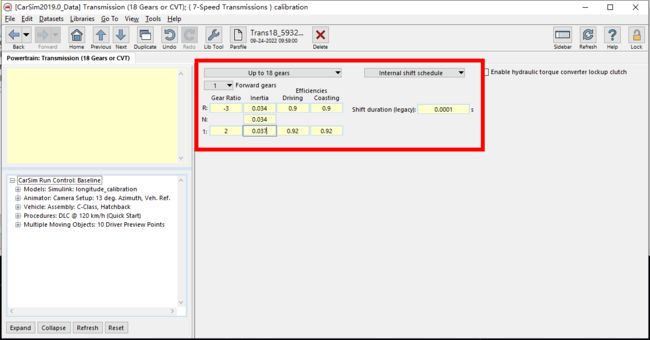
 新建一个变速器模型

 将传动比，惯量和效率都改成如下，和电机匹配

 进入发动机配置，可以通过更改发动机曲线来模拟电机，也可以用Simulink

设置好后，一定要Send to simulink，要不然都白设置了

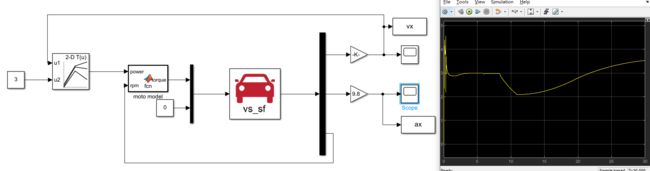
设置油门给1，然后速度和加速度都转换好

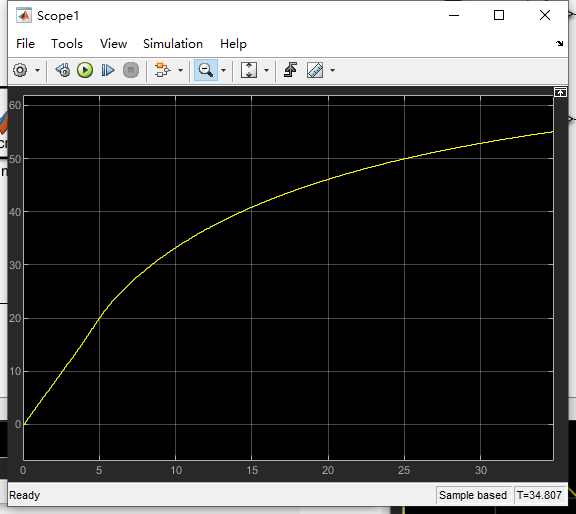
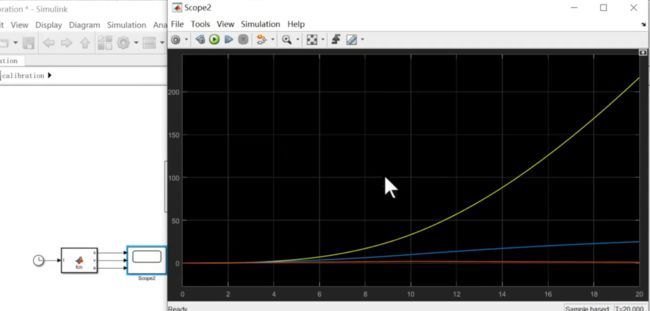
 得到速度和加速度曲线，

 最大速度超过45m/s，符合家用车最高车速

油门调成0.1就不会那么快了

 油门调成0，仍然有速度，因为发动机有怠速

 怠速设置在发动机曲线内，750rpm

 以前的电动机无怠速，现在的电动机都给个怠速，因为如果没有怠速，电机加速度过大，启动速度过大会不平顺。我们这里改成0改成750都行，选择不改。

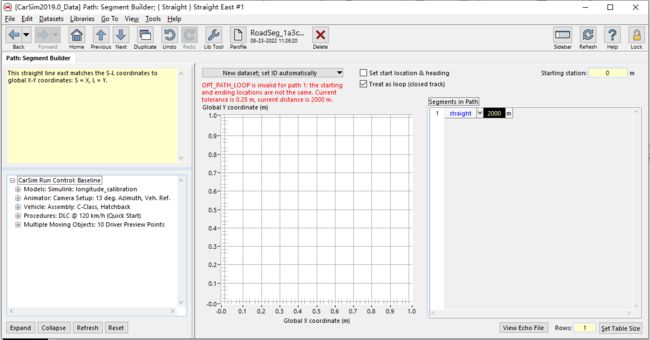
下面是路面修改，不需要之前的弯道，只需要一个2000m的道路即可（注意这里把loop取消勾，然后把前面path终点也改成2000，否则后面simulink报错）

 最后再把Simulink的文件名改一下

OK，至此准备工作完毕，具体的仿真后续第十讲会做

第十讲 油门刹车标定表的制作

一、理论部分

找到油门和v，a对应的关系

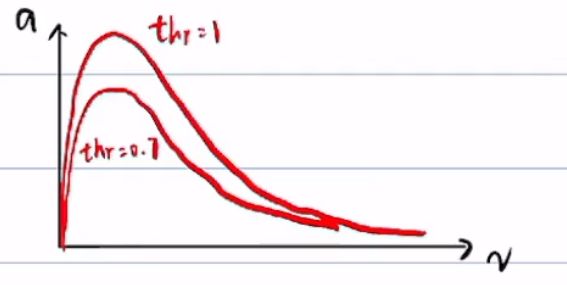
 做实验，踩不同的油门，得到不同的v，a曲线

对于一个thr，不同的时间t得到一系列va点，v，a可以合并，得到v，a曲线

 不同的thr会得到不同的va曲线，

 使用不同的thr做实验，可以得到一个三维曲面

通过做实验，得到大量的（v，a，thr）的三维点，从而拟合出thr = f(v,a)

f(v,a)叫做模型（深度学习术语）

标定表的制作

二、油门标定表制作

来到CarSim把刹车制动压力加上去

来到Simulink，首先给mux加一个输入（刹车，这里设为0），然后函数输入的油门用一个变量来表示，使用to workspace创建两个变量vx和ax

 准备就绪后，就开始写标定算法，回到matlab创建一个文件

 这个时候vx和ax就传进matlab里面了，simulink里面也能看到

 

 这时候发现采样太密了，改成0.1秒采样，注意这里要点apply，否则matlab报错

 接下来开始画表

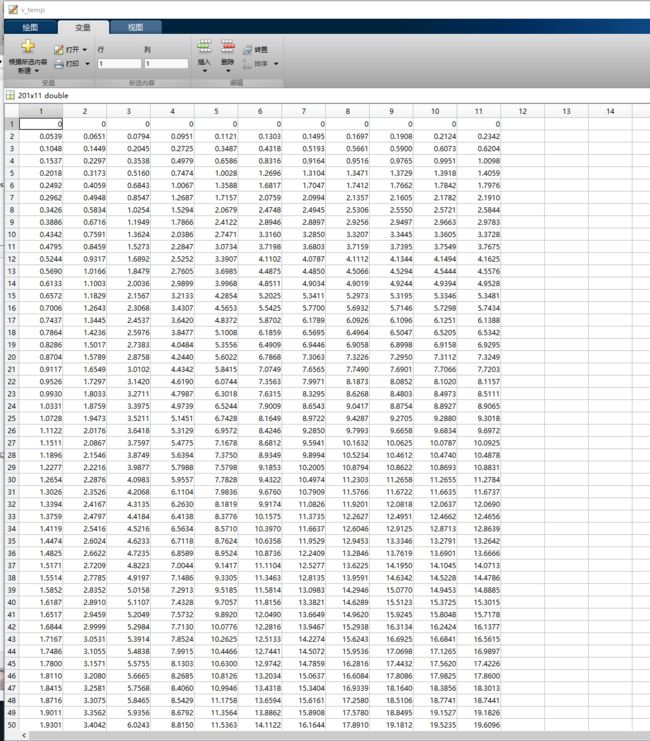
在matlab中使用以下代码，

thr = 0;  %初始化油门
for i = 1:11
    sim('calibration');
    v_temp(:,i) = vx.data;
    a_temp(:,i) = ax.data;
    thr_temp(:,i) = ones(length(vx.data),1)*thr;
    thr = thr + 0.1;
end

注意，这代码运行时间比较长，而且如果设置的时间过长的话，车速很快时，会率先到达2000m停下来，此时矩阵维度不一致会报错，所以将仿真时间截至调到30s以内

 跑完之后合并起来

% 合并，一定要转成行向量再合并，否则会导致合并失败
v = v_temp(:,1)';
a = a_temp(:,1)';
tr = thr_temp(:,1)';
for i = 2:11
    v = [v, v_temp(:,i)'];
    a = [a, a_temp(:,i)'];
    tr = [tr, thr_temp(:,i)'];
end

然后再拟合

%拟合
F = scatteredInterpolant(v',a',tr');% 转成列向量
vu = 0:0.1:50;
au = 0:0.1:5;
table = zeros(length(vu),length(au));
for i = 1:length(vu)
    for j = 1:length(au)
        table(i,j) = F(vu(i),au(j));
    end
end

运行之后得到table

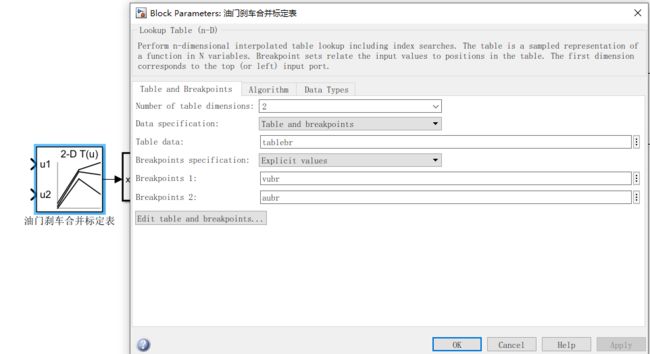
 接下来回到Simulink，使用2D lookup table拟合

然后改成au，vu和table，

 接下来点击Edit table and breakpoints查看拟合图像

 在Simulink内连接好速度和加速度，给1的加速度，点击run，得到其实际加速度也差不多为1

 改成3后，发现刚开始还可以正常跑，后面就不对了，因为油门超过1了，实际上油门最大时1

 这个table是用不超过1的油门来拟合的，所以需要加限制，在加一个延迟模块防止代数环

下面是速度控制，控制在10，注意这里加速度输入为车速与控制速度相减

 如果直接用车的加速度输入的话，结果不准确。

原因，速度与加速度不匹配，要让加速度慢慢降低至0。上面使用目标速度与实际速度相减的信号作为输入，这样会让加速度慢慢降到0，匹配上了，控制效果就会好很多。

无论是速度控制还是加速度控制，都要匹配，不能乱写。

三、刹车标定表制作

刹车标定和油门差不多

首先进入Simulink，油门设置为0，刹车设置一个变量

 初速度设置为最快的速度，这里设置为180

 send to simulink，开始写代码（油门和刹车的差不多），这里设置为0-8s的数据

brake = 0;  %初始化油门
for i = 1:80
    % 该程序非常耗时，如果需要更多更密集的数据，请先测试
    sim('calibration');
    v_temp(:,i) = vx.data;
    a_temp(:,i) = ax.data;
    brake_temp(:,i) = ones(length(vx.data),1)*brake;
    brake = brake - 0.1;
end

合并，80个数据进行合并

% 合并，一定要转成行向量再合并，否则会导致合并失败
vbr = v_temp(:,1)';
abr = a_temp(:,1)';
br = brake_temp(:,1)';
for i = 2:80
    vbr = [vbr, v_temp(:,i)'];
    abr = [abr, a_temp(:,i)'];
    br = [br, brake_temp(:,i)'];
end

拟合，这里注意加速度为负的（刹车），v和a都为单调递增的，否则不识别

%拟合
F = scatteredInterpolant(vbr',abr',br');% 转成列向量
vubr = 0:0.05:50;
aubr = -8:0.05:0;  %注意这里加速度和之前不一样，为负的
tablebr = zeros(length(vubr),length(aubr));
for i = 1:length(vubr)
    for j = 1:length(aubr)
        tablebr(i,j) = F(vubr(i),aubr(j));
    end
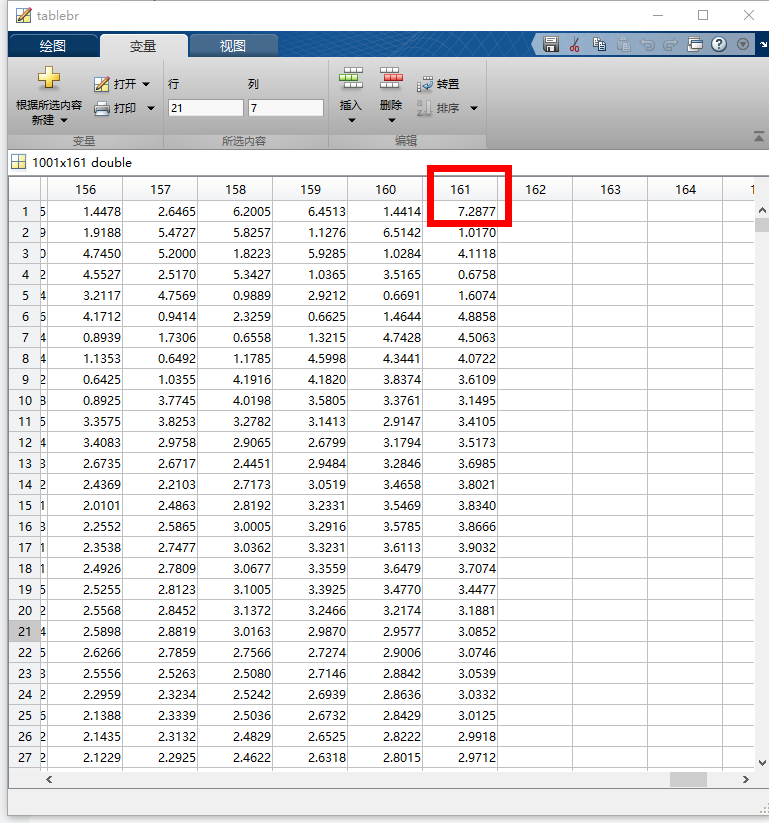
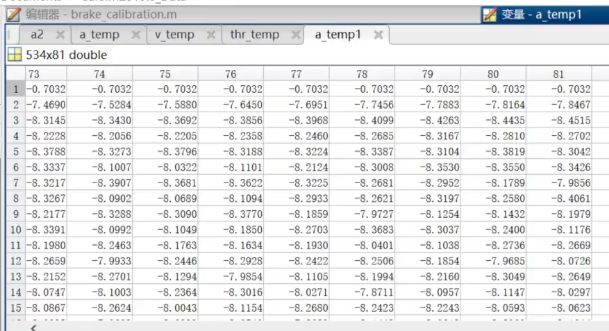
end

点击运行，程序很耗时，跑完得到tablebr ，竖着为速度0-50，横着为加速度-8到0

最后一列的数值突然变得很大，对应的是v和a=0的情况，停车状态，这个时候任意制动都会导致a=0或者v=0，这个点是所有曲线的交点，有奇异性，matlab取了个平均值。这里改一下，改成0.3，假设仅有手刹。（注：这里图有点问题，因为代码写的有点错误，实际161列第二行开始应该为0.3左右，把第一行也改成0.3即可）

 再设置一个lookup2D，把我们的数据输入进去

 设置刹车加速度为-3，看看效果

 效果不错，以-3加速度制动，然后停车后加速度为0。

以目标速度为0，然后当前速度与目标速度相减输入给加速度，这样也可以

注意加一个制动压力限制，最大9最小0MPa

 最后速度与加速度都收敛至0

 可以返回CarSim查看车辆运行状态

第十一讲 纵向双PID控制

一、前置准备

首先，这里开始使用CarSim 2019版本，纵向控制没法用2016版本。

变速器调整：换成一个挡位，然后换挡时间调短

 初速度为0，仿真时间调长一点，这里设置为40S

这里不要忘记吧刹车和转向都关掉，这些都由我们自己在simulink自己设置，

然后把道路改成Double Lane，随便设置一个长度，这里设置成5000m

接下来Send to Simulink

首先要做的是把油门和刹车做到一张表上，会自动插值，这样会更加平顺

设置一个变量x为油门刹车，x大于0为油门，小于0为刹车，使用一个函数用来判断

function [thr,brake] = fcn(x)
% 正数代表油门，负数代表刹车
%不允许同时踩油门和刹车
if x  >= 0
    thr =x;
    brake = 0;
else
    thr = 0;
    brake = -x;
end
end

接下来是标定代码（油门和刹车分开写，因为初速度不一样）

thr_calibration.m 油门采集数据代码

x = 0;  %初始化油门
for i = 1:21
    sim('calibration');
    v_temp(:,i) = vx.data;
    a_temp(:,i) = ax.data;
    thr_temp(:,i) = ones(length(vx.data),1)*x;
    x = x + 0.1;
end

% 合并，一定要转成行向量再合并，否则会导致合并失败
v = v_temp(:,1)';
a = a_temp(:,1)';
tr = thr_temp(:,1)';
for i = 2:length(v_temp(1,:))
    v = [v, v_temp(:,i)'];
    a = [a, a_temp(:,i)'];
    tr = [tr, thr_temp(:,i)'];
end

brake_calibration.m 刹车采集数据代码

% 启动前检查CarSim的初速度是否为180
x = 0;  %初始化刹车
%%% 刹车的初速度一定要比较高，180km/h，144km/h
for i = 1:81
    % 该程序非常耗时，如果需要更多更密集的数据，请先测试
    sim('calibration');
    v_temp1(:,i) = vx.data;
    a_temp1(:,i) = ax.data;
    brake_temp1(:,i) = ones(length(vx.data),1)*x;
    %%% 这里是为了消除奇异性，因为无论brake=1还是2，最后都会导致车的v=0，a=0，这将导致多值性
    for j = 1:length(v_temp1(:,i))
        if v_temp1(j,i)<0.01
            brake_temp1(j,i) = 0;
        end
    end
    x = x - 0.1;
end

% 合并，一定要转成行向量再合并，否则会导致合并失败
vbr = v_temp1(:,1)';
abr = a_temp1(:,1)';
br = brake_temp1(:,1)';
for i = 2:80
    vbr = [vbr, v_temp1(:,i)'];
    abr = [abr, a_temp1(:,i)'];
    br = [br, brake_temp1(:,i)'];
end

二、油门和刹车标定表制作

首先回到CarSim把初速度改成0，然后运行油门代码获得油门标定表

然后再回到CarSim把初速度改成180，然后运行刹车代码，获得刹车标定表

刹车标定表第一行全部都是-7.032，由于初始化问题，我们把第二行数据赋值给第一行

 加上代码

a_temp1(1,:) = a_temp1(2,:);

把上面Sim部分注释掉，然后重跑一下

代码generate_callibration.m（把油门和刹车都合并起来）

v2 = [v,vbr];
a2 = [a,abr];
br2 = [tr,br];

%拟合
F = scatteredInterpolant(v2',a2',br2');% 转成列向量
vubr = 0:0.05:50;
aubr = -8:0.05:5;  %注意这里加速度为-8到正5
tablebr = zeros(length(vubr),length(aubr));
for i = 1:length(vubr)
    for j = 1:length(aubr)
        tablebr(i,j) = F(vubr(i),aubr(j));
    end
end

在Simulink把这个表使用lookup2D设置好

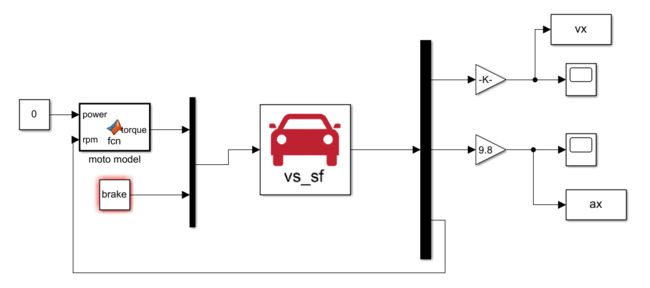
 把表，转换模块，电机模型整合一下。输入输出变量名设置好

把CarSim初速度改成0，然后Send一下

三、纵向速度PID控制仿真

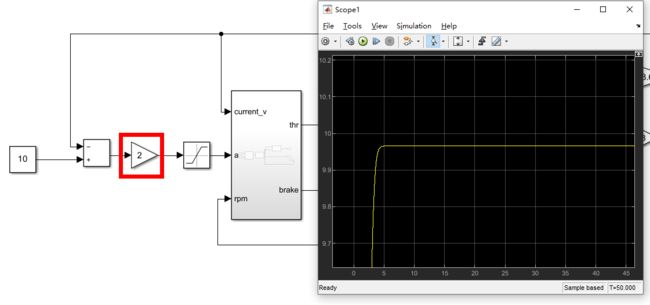
假设我们要控制加速度为10，使用简单的pid控制：期望速度-当前速度作为加速度进行输入

 仿真查看v运行结果，发现没反应，因为我们加速度没有给限制，表格内没有10这么大的加速度

 加一个限制

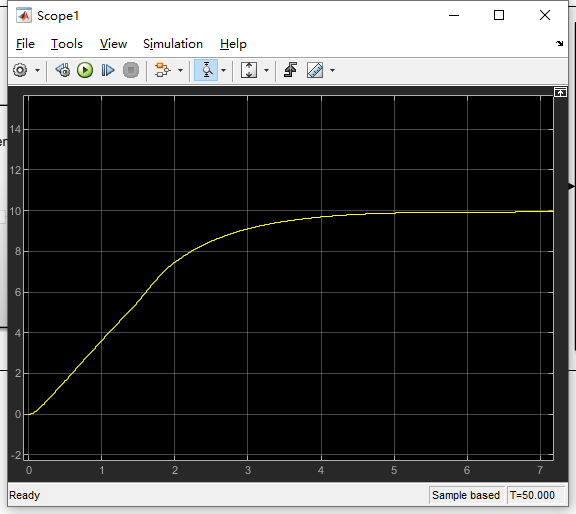
这个时候在运行，查看v确实有这个控制效果

 仔细看发现并没有到10，因为接近10的时候加速度平缓导致不加速了

 改进办法：加一个比例项，PID的P就是比例，I是积分，D是微分

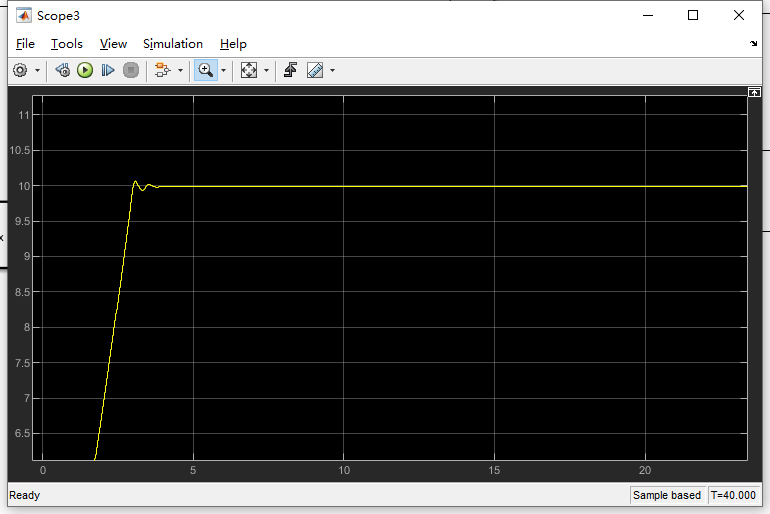
 可以看到，收敛速度更快，结果也好一些。P可以加快收敛

比例项也不是越大越好，这里调到10，发现出现超调。

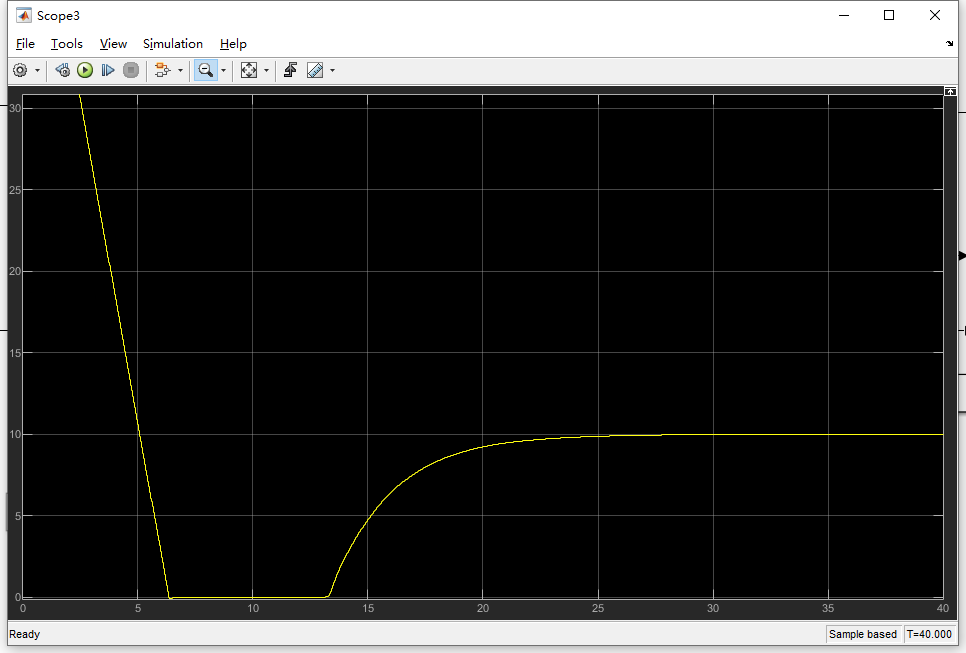
 把比例改成3，然后看下180减速到10会怎么样，可以看到发生震荡

改成pid，这里给0.1积分，发现会出现超调，但是最后还是会收敛到10

I主要目的：消除稳态误差，但是可能会引起超调

 I改成1后，发现超调严重，但是仍然能回到10，因为I存在就会对误差消除

 现在吧积分去掉，然后加一点微分D，微分的作用是抑制超调

这里放大并与上面不加微分的对比，发现震荡和超调被抑制

所以如果误差不是特别大的情况， 一般用PD即可，因为I会引起超调。

下面设计一段真实的轨迹，在Simulink中新建一个函数

function y = fcn(t)
if t < 10
    s = 0.1* t^3/3;
    v = 0.1*t^2;
    a = 0.2*t;
else
    a = 2 - 0.1*(t-10);
    v = 2*t - 0.05*(t-10)^2-10;
    s = t^2 - 0.05*(t-10)^3/3-10*t+100/3;
end
end

检测一下是否连续

 速度一直在增加，所以仿真时间要加长，这里设置到60

此外要把车的坐标输出出来

接下来回到Simulink，速度和位置都需要满足约束，所以把速度和位置的误差都输入进去，位置PID限制±10，此外加速度信号也连上，这样双PID的纵向控制就搭建完了。

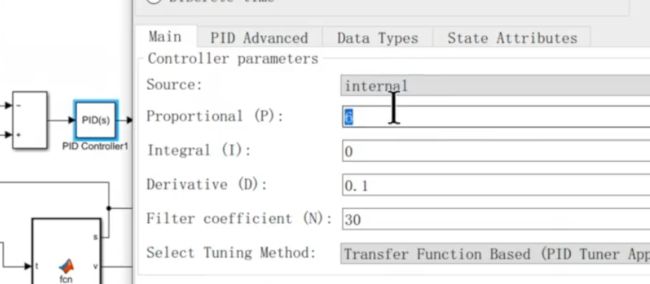
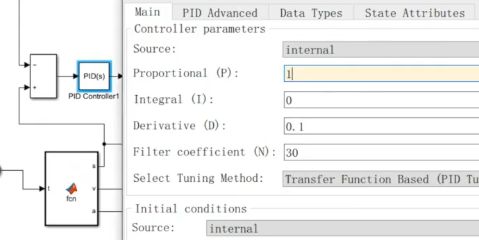
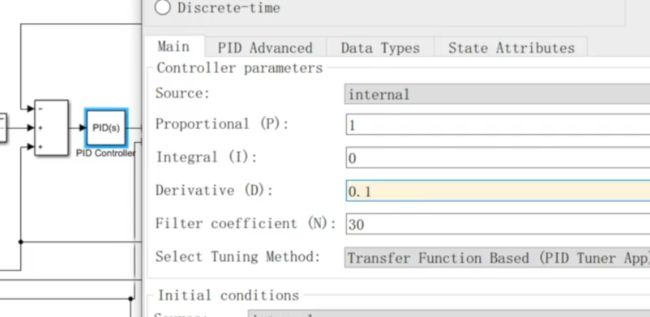
 注意这里的PID参数为比例6，积分0，微分0.1

 查看结果，位置还可以

 速度和加速度就不太行

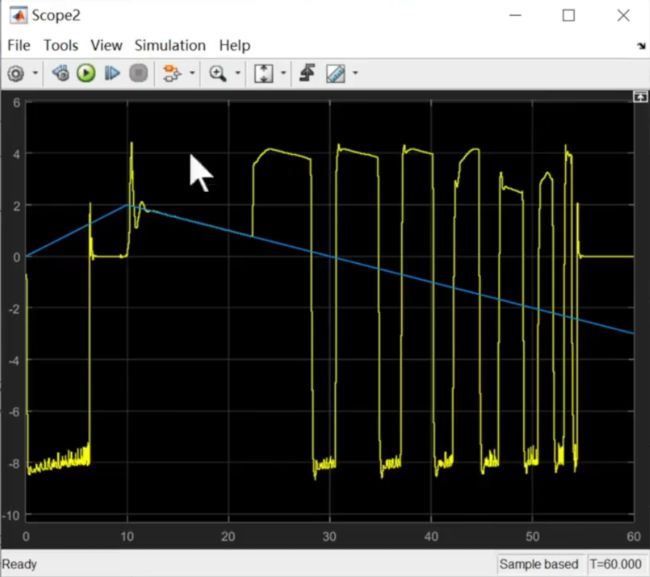
 可能是初速度的缘故，现在把初速度调成0，看下结果

可以看到位置还可以

 加速度不咋样

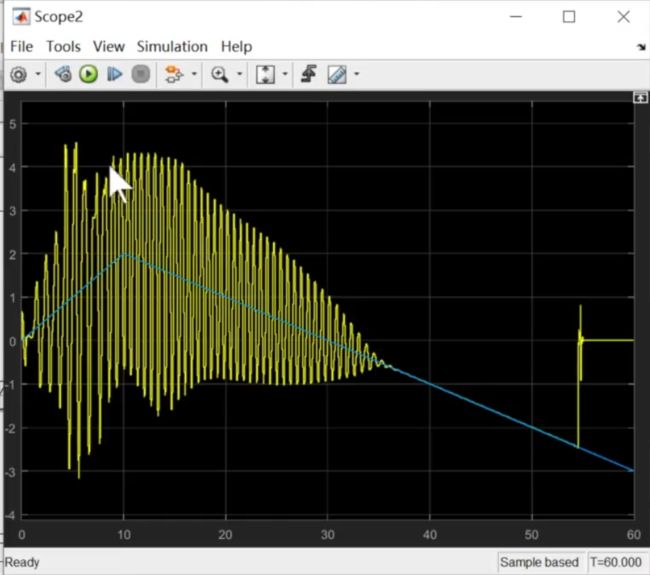
 速度有点“画龙”，一会儿大一会儿小

下面把速度PID的比例项调小点，调成2 

速度“画龙”的现象得到改善 

 加速度也比较好，后面的波动为停车后的

但是加速度前面还不太好，需要调参，直接给出参数

速度PID这样调

 位置PID这样调

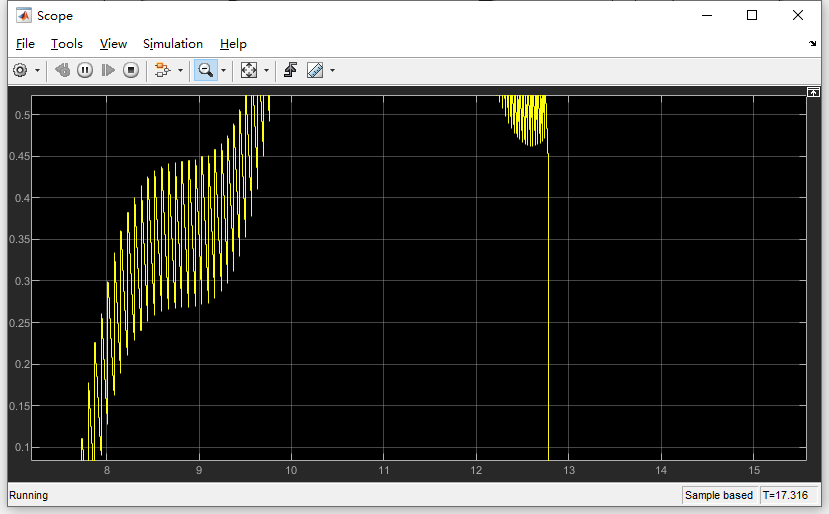
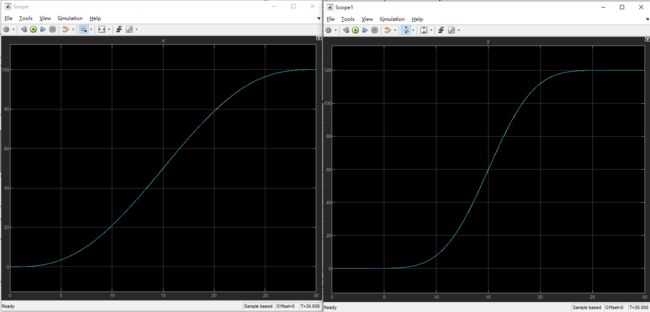
速度和加速度结果如图

 最后打包一下

第十二讲  横纵向综合控制完结

1-2 开篇，运动学方程

3-8 横向控制 LQR

9-11 纵向控制 双PID

12 横纵向控制，规划接口

运动学方程：，适用于低速情况，转角大小均可

LQR适用于小转角，低速高速均可以

所以一般在自动泊车等低速大转角的场景用运动学方程控制

一、规划接口

控制模块功能：接受一条规划的轨迹，让车按照规划的轨迹运动。首先得有规划，然后在进行横纵向控制。

注意这里是轨迹规划，不是路径规划，在自动驾驶里面，路径只会告诉该怎么走，与时间无关，而轨迹规划包含时间，速度，加速度，曲率等信息。

轨迹规划：x(t)，y(t)。（先做直角坐标系下的，由简单开始）

假设有下面的坐标系，起点在原点，终点在（100，10）处

 那么有停车场景

 或者驶入场景（终点有速度20）

 或者超车场景，起点速度为10，终点速度为20

今天就研究给定起点终点速度，加速度信息的规划。（最简单，最常用，覆盖大部分直线场景，但是不能做转弯和掉头，转弯掉头必须在自然坐标系下）。

这个地方的规划主要是为了控制服务。

规划任务可以描述为一个数学问题：设计一条合适的x(t），y(t)，满足始末的边界条件：

其中，T为耗费的时间

机器人领域有这种算法，但是无人驾驶不能直接照搬，因为车不能单独做横向运动，横向运动通常由纵向运动诱发

规划的轨迹有切线，曲率，加速度，速度的限制

 如果在起点建立一个直角坐标系，那么对也有要求

 汽车规划的边界条件为

机器人的x与y都与时间相关，而无人车不能做纵向运动，所以y和x有关

仅仅用y'做规划还不够，y与x相关，要把它弄成与时间相关

所以还需要y(t)与y(x)的转化

求y'和y''的时候使用复合求导

 边界条件为

先算出y(x)再转化为y(t)

对于x(t)使用五次多项式

 五个系数正好对应5个边界条件

对于y(t)也使用五次多项式

 因为y也有五个边界条件

通过边界条件求出多项式系数a0-5，b0-5

通过解出y(t)，y'，y''

横向控制与规划的接口

第八讲横向控制中有，，，

其中xr,yr代表匹配点，代表轨迹切线与x轴的夹角，代表轨迹曲率

xr,yr就是规划器中的x(t)，y(t)。

 ，可用下式算出

纵向控制与规划的接口

在横向控制里有，es为下图红色向量在蓝色向量上的投影

纵向误差：目标点与当前点之间的误差。在此图中es作为误差应为正，所以横向控制的es输入到纵向应该加一个负号

速度误差：，在横向控制中有

 期望加速度

逻辑梳理

首先根据规划获得x(t)，y(t)

根据x(t)，y(t)我们可以得到

 根据这些我们可以得到

 纵向控制前两个是从横向控制得到，实际输入只有后三个

二、代码实践部分

首先是横向控制和纵向控制代码和模型文件

ch8和ch11的代码和模型复制到CarSim目录下面

然后打开Matlab

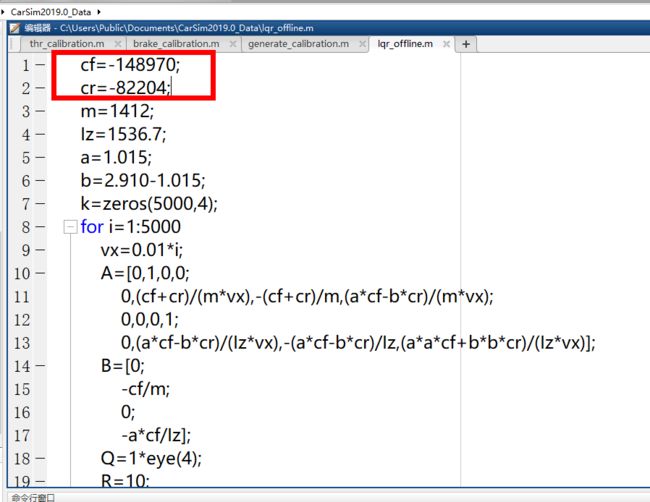
注意lqr这里的cf和cr要改一下，因为需要更精确的模型，不能像第八讲那样混一下，

 必须要计算出每个轮子精确的垂向力，然后通过垂向力查表查到侧偏刚度大概估算出来

 不要忘了加这句话

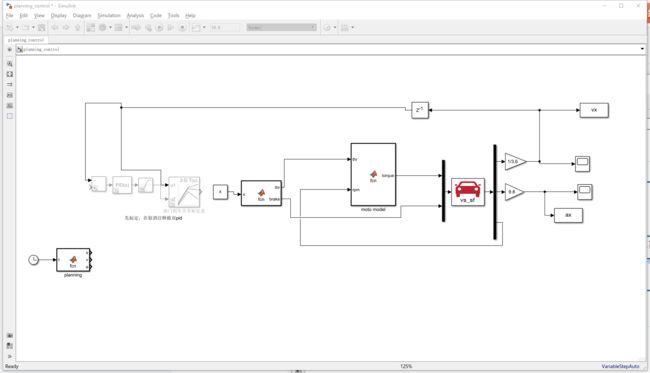
 重新设置一个新的模型 planning_control

 INPUT设置

 注意这里一定要调成replace

 OUTPUT设置

 新建Simulink模型然后Carsim绑定这个模型

 仿真时间改成40S，初速度为0，刹车和转向不开启

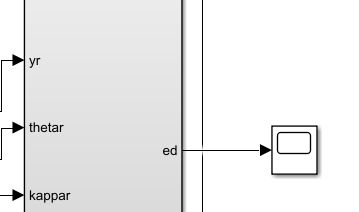
把纵向控制模型复制进去

 下面进行标定，这里把输入输出改成上一讲的输入输出，

解除注释，然后再重复上一讲的内容进行table制作

如果懒得再弄一遍，这里直接上链接

油门刹车标定表.zip - 蓝奏云

把mat文件在matlab中加载一下

接下来把纵向双PID搭建好，然后把输出改成7个，删掉标定的东西，然后标上实际输出

 接下来把左下角的规划模块改一下，改一下输出

 接下来把位置PID的输入改成es，然后把输出加上单位换算（注意yaw那里是pi/180，之后才发现错误），在进行一些调整

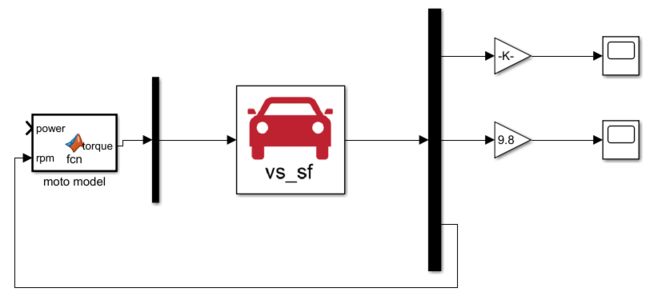
 接下来把如图所示的模块都合并一下

要把速度当成电机输入，所以下面写一个速度函数

function v = fcn(vx,vy)
    v = sqrt(vx^2 + vy^2);
end

然后我们把规划重新写一遍

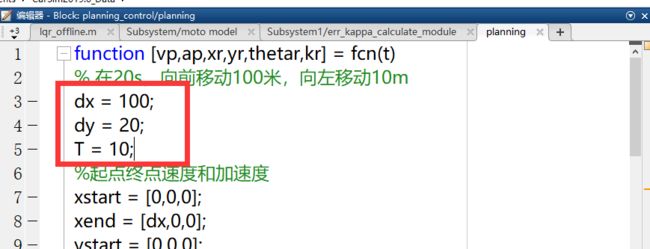
function [vp,ap,xr,yr,thetar,kr] = fcn(t)
% 在20s，向前移动100米，向左移动10m
dx = 100;
dy = 10;
T = 20;
%起点终点速度和加速度
xstart = [0,0,0];
xend = [dx,0,0];
ystart = [0,0,0];
yend = [dy,0,0];
% 设置多项式系数向量
a = zeros(1,6);
b = zeros(1,6);
%解x的系数
a(1) = xstart(1);
a(2) = xstart(2);
a(3) = xstart(3)/2;
A1 = [T^3,       T^4,      T^5;
          3*T^2,   4*T^3,   5*T^4;
          6*T,       12*T^2,  20*T^3];
B1 = [xend(1)-a(1)-a(2)*T-a(3)*T^2;
          xend(2)-a(2)-2*a(3)*T;
          xend(3)-2*a(3)];
xs = inv(A1)*B1;
a(4) = xs(1);
a(5) = xs(2);
a(6) = xs(3);
%解y的系数
b(1) = ystart(1);
b(2) = ystart(2);
b(3) = ystart(3)/2;
A2 = [dx^3,       dx^4,      dx^5;
          3*dx^2,   4*dx^3,   5*dx^4;
          6*dx,       12*dx^2,  20*dx^3];
B2 = [yend(1)-b(1)-b(2)*dx-b(3)*dx^2;
          yend(2)-b(2)-2*b(3)*dx;
          yend(3)-2*b(2)];
ys = inv(A2)*B2;
b(4) = ys(1);
b(5) = ys(2);
b(6) = ys(3);
% 求x点，x两点，y‘，y’‘以及曲率，vp，ap
xr = a(1) + a(2)*t + a(3)*t^2 + a(4)*t^3 + a(5) *t^4+a(6)*t^5;
yr = b(1) + b(2)*xr + b(3)*xr^2 + b(4)*xr^3 + ab(5) *xr^4+b(6)*xr^5;
xr_dot = a(2) + 2*a(3)*t + 3*a(4)*t^2 + 4*a(5) *t^3+5*a(6)*t^4;
yr_dx =  b(2) + 2*b(3)*xr + 3*b(4)*xr^2 + 4*ab(5) *xr^3+5*b(6)*xr^4;
yr_dot = yr_dx *xr_dot;
thetar = atan(yr_dx);
xr_dot2 = 2*a(3)+6*a(4)+ 12*a(5) *t^2+20*a(6)*t^3;
yr_dx2 = 2*b(3)+6*b(4)+ 12*b(5) *xr^2+20*b(6)*xr^3;
yr_dot2 = yr_dx2*xr_dot^2 + yr_dx*xr_dot2;
kr = yr_dx2/((1 + yr_dx^2)^1.5);
vp = sqrt(xr_dot^2 + yr_dot^2);
ap = sqrt(xr_dot2^2 + yr_dot2^2);
end
    

重新连一下规划的线

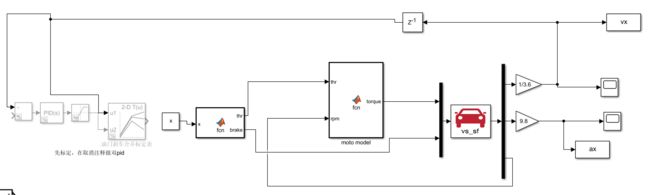
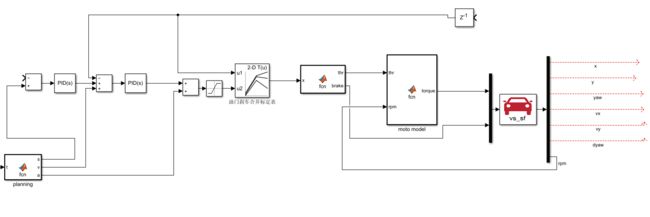
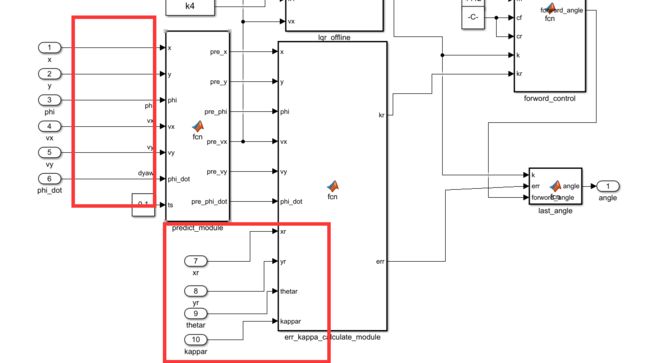
 接下来把横向控制加进来

打开横向控制的模型

 下面对主要模块进行修改

 去掉单位换算，然后把xr，yr，thetar，kappar都设置为外部输入

 接下来更改误差计算模块，增加输出es和s_dot，然后去掉寻找dmin的过程，因为我们这里的规划不是之前那样给好轨迹

function [kr,err,es,s_dot] = fcn(x,y,phi,vx,vy,phi_dot,xr,yr,thetar,kappar)
    tor=[cos(thetar);sin(thetar)];
    nor=[-sin(thetar);cos(thetar)];
    d_err=[x-xr;y-yr];
    ed=nor'*d_err;
    es=tor'*d_err;
    %projection_point_thetar=thetar(dmin);%apollo
    projection_point_thetar=thetar+kappar*es;
    ed_dot=vy*cos(phi-projection_point_thetar)+vx*sin(phi-projection_point_thetar);
    %%%%%%%%%
    ephi=sin(phi-projection_point_thetar);
    %%%%%%%%%
    ss_dot=vx*cos(phi-projection_point_thetar)-vy*sin(phi-projection_point_thetar);
    s_dot=ss_dot/(1-kappar*ed);
    ephi_dot=phi_dot-kappar*s_dot;
    kr=kappar;
    err=[ed;ed_dot;ephi;ephi_dot];
end

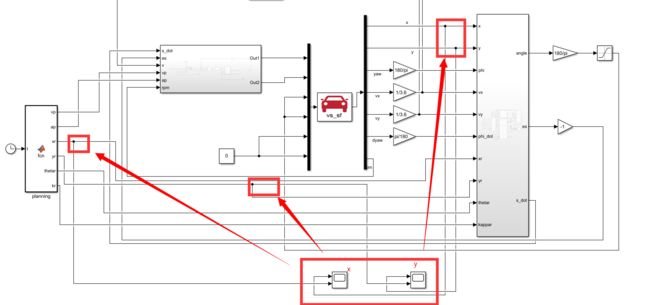
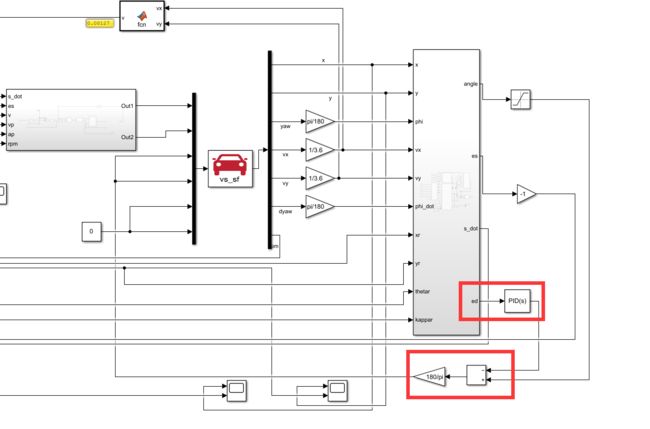
接下来退出来，先把该连的连起来，然后把输入改成6个，增加前后轮转角，后轮转角设置为0，然后给angle加上单位换算和±1的限制，给es乘以-1输入到纵向控制

接下来到纵向控制内，给es增加限制±10，然后PID参数改成如下

 接下来增加2个示波器，比较一下实际x,y和规划的xr,yr有多大误差 

 进入matlab运行lqr_offline获得k

接着运行Simulink 

报错，原因：仿真时间过长

Index exceeds array dimensions. Index value 5000 exceeds valid range [1-4999] of array k1. Error in 'planning_control/Subsystem1/lqr_offline' (line 6) k=[k1(index),k2(index),k3(index),k4(index)];

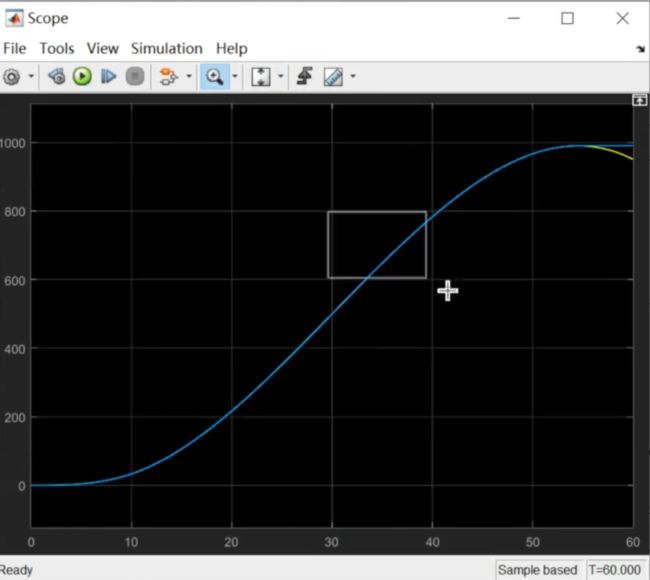
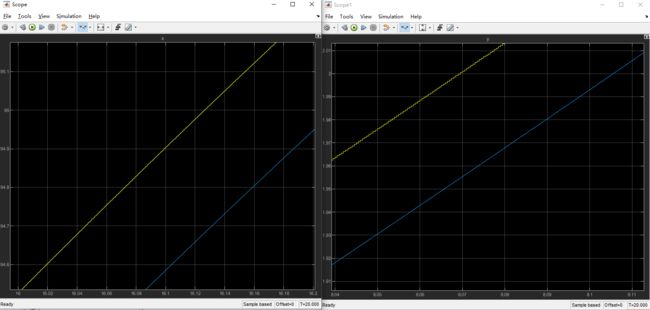
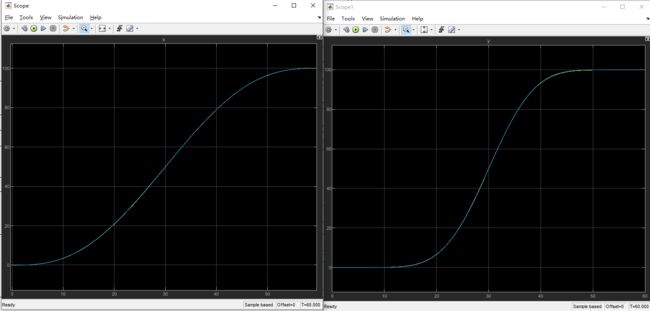
调短一点再run，然后查看scope，发现x，y基本上重合

放大看还是有0.几的误差，仿真中对误差的要求是0.0几m以内才能保证实车上面有误差和噪声的条件下精确

原因分析：在planning模块中，ap可正可负

所以将其中的

ap=sqrt(xr_dot2^2+yr_dot2^2);

改为ap根据xr_dot2的正负改变

if xr_dot2>=0
    ap=sqrt(xr_dot2^2+yr_dot2^2);
else
    ap=-sqrt(xr_dot2^2+yr_dot2^2);
end

调好后再run一下发现横向误差还是大，纵向误差可以接受

发现是angle这里应该先限制再单位转换

为了能直观看到横向误差，我们在LQR模块把ed输出出来

 差不多ed是0.04左右

 去规划中把速度调快，10s内完成

 发现高速下性能不怎么样

 原因：加速度ap超了

下面试一下低速大转角

 回到CarSim把仿真时间改到80

 再回到simulink加一个scope查看速度

 表现得很好

横向纵向误差均在0.05以内

lqr需要在小转角，加速度不能超了，一般在2-3以内

一般横向误差控制的不好，原因有三

一是侧偏刚度自己估的，不太准，前轮后轮垂向力不一样，因为加速度导致轴荷转移，垂向力不一样导致侧偏刚度变化

二是因为LQR基于二自由度模型，自行车模型，本来就有简化性，本来就有误差

三是汽车固有特性：转向不足

一般来说仿真达到厘米级可以接受，实车需要达到0.1m可以接受，因为实车有误差和噪声

如果横向误差过大，需要给Q更大的惩罚值，即给ed更大的惩罚值，尽可能让ed收敛到0，而e_phi不可能收敛到0，因为e_phi的稳态误差就是beta

一般来说改三个，一个是转向不足，二一个是LQR的侧偏刚度，三一个是调LQR的Q

三、转向不足

最后讲一下转向不足导致的横向误差过大问题

转向不足和过度转向都是实车会发生的情况，即实际转角小于或者大于理论转角

 为什么会发生转向不足\过度呢

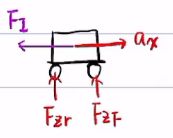
如果前后轮侧向力不匹配，质心处会存在力矩

 如果，质心无力矩，导致中性转向

如果，质心有正力矩，导致过度转向

如果，质心有负力矩，导致不足转向

一般市面上买到的车都是转向不足，为了安全考虑，一般赛车调校成中性转向，因为赛车天生高速下有过度转向的趋势

那么如何处理呢？

方法：使用PID，给误差做个积分，再补偿到前轮转角上去

这里PID给I设置为3，其他均0。此外把单位转换放到后面去，先做减法再换算。

 因为ed为正说明方向盘打多了，就给它减掉，

下面把规划出的横向位置调的严苛一点

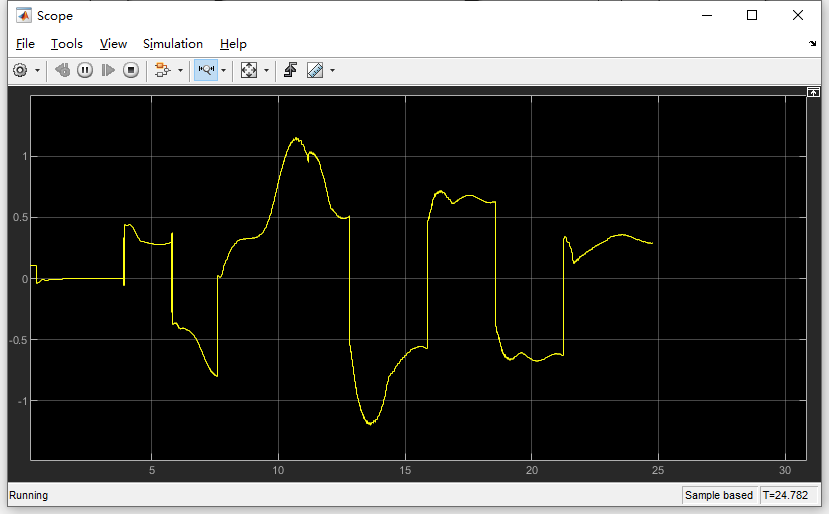
 然后仿真30秒查看结果

效果更好一点

 误差更小一些，横向误差控制在了0.02以内

查看ed ，ed已经在0.01以内了

 这里因为模型本来比较准，所以提升不大，但是对于实车而言提升比较大

到这里本课程基本结束

结论：matlab速度太慢了，而且这里只有纯控制无规划，加上规划，决策等模块更慢，所以实车还是需要C++和linux，因为速度会更快