Uplift Model

0.uplift modelling相关理论

• 定义：$\tau (x)=E[Y_i(1)|X]-E[Y_i(0)|X]$，单个样本在有干预和没有干预两种情况的表现(potential outcome)的差值
• 目标：识别出营销敏感人群
• 挑战：无法同时观测单个样本在有干预和没有干预两种情况的表现
• 理论依据：当CIA假设成立时($X_i\perp T_i$，样本特征X和T独立)，$ATE=\tau (X_i)=E[Y_i(1)|X]-E[Y_i(0)|X]=E[Y_i(1)|X_i,T_i=1-E[Y_i(0)|X_i,T_i=0]$
• 需满足假设：CIA假设成立时($X_i\perp T_i$，样本特征X和T独立)，可通过随机化RCT实验实现
• 直观理解：举例一个场景：Y 代表用户广告转化，X 是用户维度的特征，T 代表的是营销的变量 ( 1 代表有干预，0 代表无干预 )。假设我们有两群同质用户，均来自一线城市/年龄段为 25-35/女性，我们可以对其中一组用户进行广告投放，另外一组不进行任何干预，之后统计这两群人在转化率上的差值，这个差值可以被近似认为是具备同样特征的人可能的平均因果效应。所以 Uplift Model 本质是从T=1/T=0两组无偏样本中学习ATE，通过模型的泛化性对未知样本进行预测。
  

1.uplift modelling 常用方法

1.1 tree-based

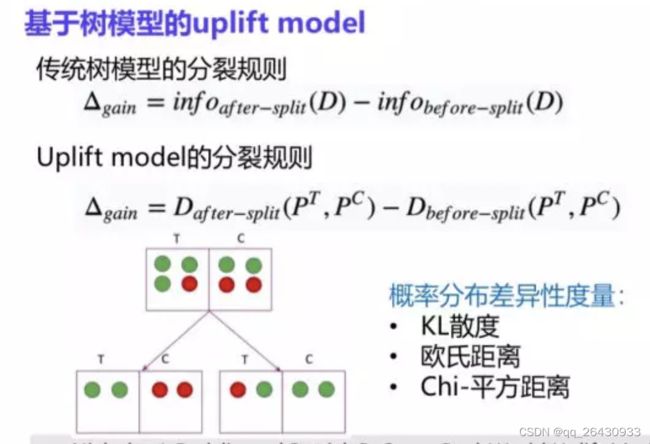
和机器学习中的树基本一样(分裂规则、停止规则、剪枝），核心为分裂规则，根据每个叶子节点的uplift，计算分裂前后的信息差异(如转化率的差异)。常用比如基于分布差异(KL、Euclidean等）；或者结合bagging、boosting技术等。

1.2 regression-based / Meta-Learner

1.2.1 S-learner和T-learner

T-learner
用两个分别base learner去模拟干预组的outcome和非干预组的outcome

• 优点是，The T-learner tries to solve the problem of discarding the treatment entirely by forcing the learner to first split on it,hence, avoids the problem of not picking up on a weak treatment variable
• 缺点是，容易出现两个模型的Bias方向不一致，形成误差累积，使用时需要针对两个模型打分分布做一定校准

S-learner
是将treatment作为特征，干预组和非干预组一起训练，

• 优点是，解决了bias不一致的问题
• 缺点是，如果本身X的high dimension可能会导致treatment丢失效果。if the treatment is very weak relative to the impact other covariates play in explaining the outcome, the S-learner can discard the treatment variable completely. Notice that this is highly related to the chosen ML model you employ. The greater the regularization, the greater the problem
  

1.2.2 X-learner

T-learner和S-learner是一种naive的方法，无法解决样本不均衡的问题、selection bias等问题。
例子
T=1组只有少量样本(as treatment is often expensive)，假设T、X和Y的关系是非线性的，且treatment effect是个常数等于1
第一步：T=1和T=0组分别构建模型
$$\begin{array}{r}rightmodel非线性:{\hat{M}}_0(X)=E(Y|T=0,X)\\ wrongmodel线性:{\hat{M}}_1(X)=E(Y|T=1,X)\end{array}$$

训练得到的${\hat{M}}_1(X)$模型非常简单，是个线性模型。因为样本少，为了防止过拟合，模型自然简单。但T=0组样本量充足，${\hat{M}}_0(X)$模型捕捉到了Y的非线性关系。$\hat{C}ATE=\hat{\tau }={\hat{M}}_1(X)-{\hat{M}}_0(X)$，是个非线性的结果，这与实际不符(实际的treatment effect是个常数等于1)。图中蓝色点是T=1组的观测Y，蓝线是${\hat{M}}_1(X)$；图中红色点是T=0组的观测Y，红线是${\hat{M}}_0(X)$

第二步：用T=0组的模型去预测T=1组的outcome，并和T=1组的观测Y相减
$$\begin{array}{r}wrongmodel非线性:\hat{\tau }(X,T=0)={\hat{M}}_1(X,T=0)-Y_{T=0}\\ rightmodel线性:\hat{\tau }(X,T=1)={\hat{M}}_0(X,T=1)-Y_{T=1}\end{array}$$

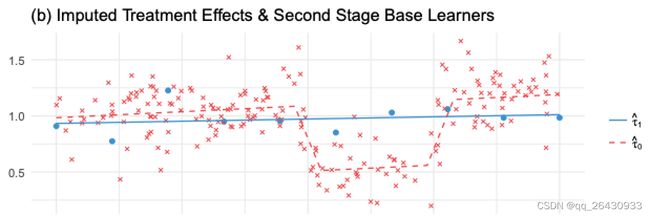
红色点是 $\hat{\tau }(X,T=0)$是用错误的线性模型${\hat{M}}_1(X)$估计出来的，该估计是错的(真实treatment effect是常数1)；蓝色点是 $\hat{\tau }(X,T=0)$是用正确的非线性模型${\hat{M}}_0(X)$估计出来的，该估计是对的，和真实treatment effect是常数1的设定相符；
将红色点和蓝色点拟合成模型：
$$\begin{array}{r}wrongmodel非线性:{\hat{F}}_{\tau 0}=E[\hat{\tau }(X)|T=0]\\ rightmodel线性:{\hat{F}}_{\tau 1}=E[\hat{\tau }(X)|T=1]\end{array}$$

第三步：得到正确的${\hat{\tau }}_1$和错误的${\hat{\tau }}_0$之后，通过倾向性得分加权最终的预估$\hat{\tau }$
$$\hat{\tau }(X)={\hat{F}}_{\tau 0}\ast \hat{e}(X)+{\hat{F}}_{\tau 1}\ast (1-\hat{e}(X))$$

T=1组样本量少，$\hat{e}(T=1|X)$的预测样本也较少，所以错误的${\hat{\tau }}_0$获得权重较低，$(1-\hat{e}(X))$接近1，所以正确的${\hat{\tau }}_1$获得较高的权重。
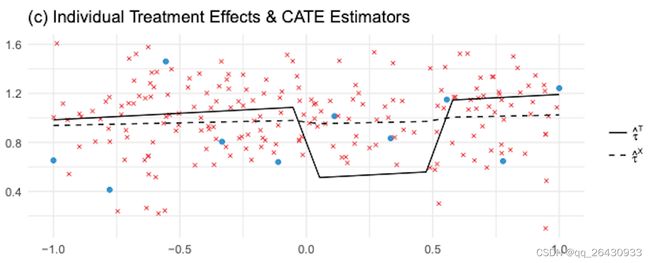
图中虚线为${\hat{\tau }}^X$，表示X-learner预测得到的$\hat{C}ATE$；实线为${\hat{\tau }}^T$，表示T-learner预测得到的$\hat{C}ATE$，可以看到X-learner的预测更接近treatment effect是常数1的设定。

2.uplift modelling 评估方法

• uplift modelling 评估难点：对单个样本的uplift ground truth未知
• 解决思路：构造两组特征相似的人群，将两组人群的表现差异作为uplift ground truth

  相似人群构造：对T=1/T=0两组群人分别预估uplift score，之后将人群按照 uplift score 进行降序排列，通过 score 分数这一桥梁，可以把两组人群进行镜像人群的对齐，之后分别截取分数最高的比如 10% 的用户出来，计算这一部分人观测转化率的差异，这个差异就可以近似地认为是分数最高的这群人真实的uplift，类似地，我们可以计算前 20%，40% 一直到 100% 的点上面的值，连线就能得到 uplift curve。

2.1 Qini Curve

$$Q(i)=(\frac{N_{t,y=1}(i)}{N_t}-\frac{N_{t,y=0}(i)}{N_c}),i=10\%,20\%,\cdots 100\%$$

• $N_t$表示实验组总样本量，$N_c$表示对照组总样本量；
• 当$i=10\%$时，$N_{t,y=1}(i)$表示实验组前10%样本中，y=1的数量，即转化人数占比；
• 如果实验组和对照组用户数量差别比较大，结果容易失真

2.2 AUUC(Area Under the Uplift Curve)

$$G(i)=\frac{N_{t,y=1}(i)}{n_t(i)}-\frac{N_{t,y=0}(i)}{n_c(i)}\ast (n_t(i)+n_c(i)),i=10\%,20\%,\cdots 100\%$$

• 当$i=10\%$时，$n_t(i)$表示实验组样本量，$n_c(i)$表示对照组样本量
• 与Qini系数相比，累积增益的分母是百分比下的实验组或对照组人数，并乘以$n_t(i)+n_c(i)$作为全局调整系数，避免实验组和对照组用户数量不平衡导致的指标失真问题。？？为什么能实现？？
  +** Qini是算的实验组和对照组转化率的差值，AUUC是算的实验组和对照组转化用户数量的绝对差值，QIni是不是要成一$N_t+N_c$???**

参考资料

21 - Meta Learners - Causal Inference for The Brave and True
阿里文娱智能营销增益模型 (Uplift Model) 技术实践
智能营销增益模型（Uplift Modeling）的原理与实践