知识图谱从0到-1的笔记——6.知识推理

开始知识图谱从0到-1，用的书是《知识图谱方法、实践与应用》，做些阅读笔记，如有错误内容，望各位指正。

知识推理

1. 推理概述

1.1 什么是推理

• 推理：通过已有的知识推断出未知知识的过程

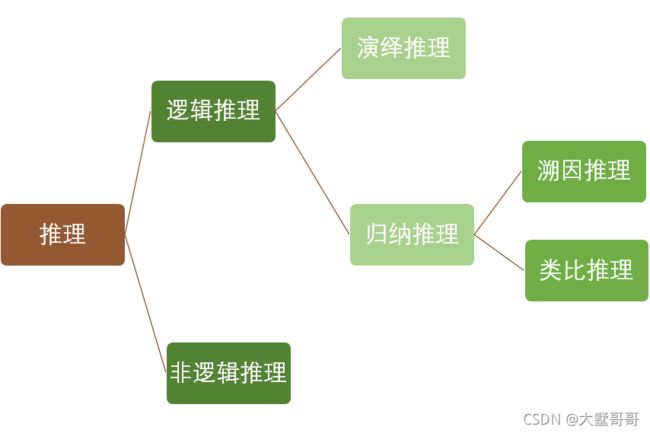
推理的方法的分类和具体方式如下图所示，其中非逻辑推理的过程相对比较模型，而逻辑推理的透明性与定义比较清晰，所以主要围绕逻辑推理展开。

1.2 逻辑推理

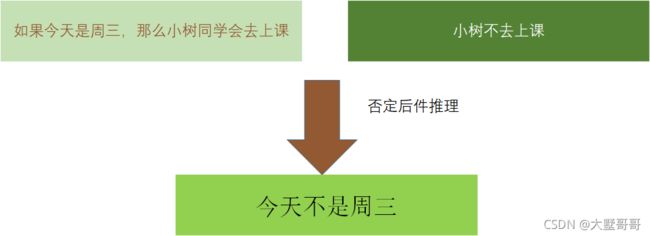
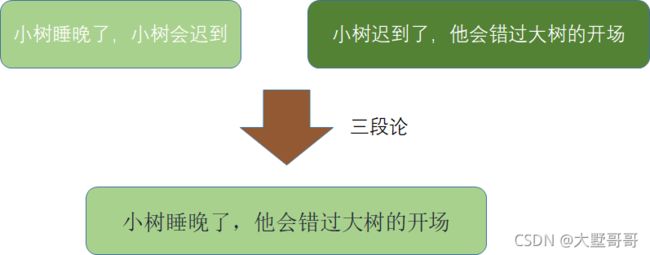
1.2.1 演绎推理

• 演绎推理：是一种自上而下的逻辑推理，是指在给定的一个或多个前提下，推断出一个必然成立的结论的过程。典型的有：肯定前件假言推理、否定后件假言推理以及三段论
  
  
  

1.2.2 归纳推理

• 归纳推理：是一种自下而上的推理，是隐喻已有的部分观察得出一般结论的过程。
• 例子：人们见到的天鹅都是白色的，那么由此推理出天鹅大概率是白色。

1.2.3 溯因推理

• 溯因推理：事在给定一个或多个已有观察事实O(Observation),并根据已有的知识T（Theory）推断出对已有观察最简单且最有可能的解释的过程。
• 例子：我们知道下雨了马路一定会湿(T)，如果观察到马路是湿的（O）；可以通过溯因推理得到很大概率下雨(E(解释))

1.2.4 类比推理

• 类比推理：只基于对一个事物的观察而进行的对另一个事物的归纳推理，是通过寻找两者之间可以类比的信息，将已知事物上的结论迁移到新的事物上的过程。
• 例子：小树同学和大树同学都是知识图谱爱好者，他们都喜欢机器学习和编程，且小树同学喜欢NLP，那么通过类比推理可以得到大树同学也喜欢NLP

1.3 知识图谱推理

面向知识图谱的推理：主要围绕关系的推理展开，即基于图谱中已有的显性事实或关系推断出未知的事实或关系。从而辅助推理出新的事实、关系、公理以及规则等

一个丰富、完整的知识图谱的形成会经历很多阶段，从知识图谱的生命周期来看，不同阶段都涉及不同的推理任务，其中包括知识图谱补全、不一致性检测、查询扩展等。

知识图谱的推理的主要技术手段可以分为两大类：

1. 基于演绎的知识图谱推理：基于描述逻辑、Datalog、产生式规则等
2. 基于归纳的知识图谱推理：路径推理、表示学习、规则学习、基于强化学习的推理等

1.3 基于演绎的知识图谱推理

1.3.1 本体推理

1.3.1.1 本体与描述逻辑

演绎推理的过程需要明确定义的先验信息，所以基于演绎的知识图谱多围绕本体。本体的一般定义为概念化的显示规约，它给不同领域提供共享的词汇。因为共享的词汇需要赋予一定的语义，所以基于演绎的推理一般都在具有逻辑描述的基础的知识图谱上展开。
目前OWL是知识图谱语言中最规范、最严谨、表达能力最强的语言。基于RDF语法，使得表示出来的文档具有语义理解的结构基础。OWL在推理问题中，有以下的一些推理问题:

1. 概念包含：例如$Mother\subseteq Women和Women\subseteq Person$,可以得到$Mother\subseteq Person$
2. 概念互斥: 例如$Man\cap Women\subseteq \perp$,可以得到$Man$和$Women$的概念是互斥的
3. 概念可满足:例如$Eternity\subseteq \perp$,可以得到$Eternity$是不可满足概念
4. 全局一致:例如公理$Man\cap Women\subseteq \perp$,可以得到$Man(Allen)和Women(Allen)$的本体是不一致的
5. TBox一致:例如包含公理$Man\cap Women\subseteq \perp ,Professor\subseteq Man和Professor\subseteq Women$的Tbox是不一致的
6. 实例测试:判定个体$a$是否是概念$C$的实例，需要判定$C(a)$是否为给定知识库的逻辑结论
7. 实例检索:找出概念$C$在给定知识库中的所有实例，需要找出属于$C$的所有个体$a$,即$C(a)$是给定知识库的逻辑结论。

1.3.1.2 基于Tableaux的本体推理方法

基于表运算（Tableaux）的本体推理方法是描述逻辑知识库一致性检测的最常用的方法。基于表运算的推理通过一系列规则构建Abox，已检测可满足性，或者检测某一实例是否存在某概念。

Tableaux运算规则(以主要DL算子举例)如下：
初始情况下，$\varnothing$是原始的Abox，迭代运用如下规则：

这里对第一个解释一下，其他的类似。第一个是说如果$C$ 和$D(x)$ 的合取是$\varnothing$，同时$C(x)$ 和 $D(x)$ 却不在$\varnothing$里，那么也就是说$\varnothing$有可能只包含了部分$C$，而$C(x)$不在里面，那么我们就把它们添加到$\varnothing$里。
下面我举个例子：
现在给定如下本体，检测实例Allen 是否在 Woman中? 即:

$Man\sqcap Woman⊑\perp$

$Man(Allen)$

检测 $Woman(Allen)？$其解决流程为:

• 首先加入带反驳的结论:
  $$Man\sqcap Woman\in \perp$$

$$Man(Allen)Woman(Allen)$$

• 初始$Abox$，记为$\varnothing$,其内包含$Man(Allen)Woman(Allen)$。

• 运用 ${\sqcap }^{+}-$规则，得到 $Man\sqcap Women(Allen)$。将其加入到$\varnothing$中，现在的 $\varnothing$为 $Man(Allen)Woman(Allen)Man\sqcap Women(Allen)$

• 运用 $⊑-$ 规则到$Man\sqcap Women(Allen)$与$Man\sqcap Woman⊑\perp$上，得到 $\perp (Aleen)$。此时的$\varnothing$包含 $Man(Allen)Woman(Allen)Man\sqcap Women(Allen)\perp (Aleen)$

• 运用$\perp -$规则，拒绝现在的$\varnothing$。

• 得出Allen 不在Woman的结论。如果$Woman(Allen)$在初始情况已存在于原始本体,那么推导出该本体不可满足!

1.3.2 基于产生式规则的方法

1.3.2.1 产生式系统

产生式系统是一种前向推理系统，可以按照一定机制执行规则并达到某些目标，与一阶逻辑类似，也有区别。产生式系统可以应用于自动规划和专家系统等领域。一个产生式系统由事实集合、产生式集合和推理引擎三部分组成。

• 事实集合：事实可描述对象，形如(type attr_1:val_1 attr_2:val_2…attr_n:val_n)，其中的type,attr_i,val_i均为原子（常量）。

  1. 例如(student name:“Alice” age:24)：表示一个学生，姓名为Alice，年龄为24。
  2. 事实也可以描述关系，（basicFact relation：olderThan firstArg：John secondArg：Alice）

• 产生式集合：有一系列的产生式组成，形如：$$IFconditionsTHENactions$$ 其中conditions是条件组成的集合（称为LHS）,actions是由动作组成的序列（称为RHS)
       
    
  LHS的形式如下：

  • 原子: 如Alice （person name:Alice）
  • 变量: 如x （person name:x）
  • 表达式: 如Alice （person age:[n+4]）
  • 布尔测试: 如Alice （person name:{>10}）
  • 约束的与、或、非操作

    

  RHS的动作种类如下三种：

  • ADDpattern: 向WM中加入形如pattern的WME
  • REMOVE i:从WM中一出当前规则第i个条件匹配的WME
  • MODIFY i (attr:spec)：对于当前规则第i个条件匹配的WME，将其对应于attr属性的值改为spec

例如：$IF(Studentname:)ThenADD(Personname:)$表示如果有一个学生名为 $?x$ ,则向事实集加入一个事实，表示有一个名为 $?x$ 的人

s

• 推理引擎：用于控制系统的执行，主要有三个部分：
  1. 模式匹配：用规则的条件部分匹配事实集中的事实，整个LHS都被满足的规则被处罚，并加入议程(Agenda)
  2. 选择规则，按一定的策略从被触发的多条规则中选择一条
  3. 执行规则，执行被选择出来的规则的RHS，从而操作WM。

下图是一个匹配规则的过程，规则为：$(typex,y),(subClassofyz)\to (typexz)$

1.4 基于归纳的知识图谱推理

1.4.1 基于规则学习的知识图谱推理

基于规则的推理具有精确且可解释的特性，规则在学术界和工业界的推理场景都有重要应用。其中规则是规则推理的核心，所以规则获取是一个重要的任务，

规则一般包含两个部分，分别为规则头（head）和规则主体（body），一般形式为：$$rule:head\leftarrow body$$

• 规则头：由一个二元的原子构成构成
• 规则主体：由一个或多个一元原子或二元原子组成
• 原子：是指包含了变量的元组，例如IsLocation（X）是一个一元原子表示实体变量X是一个位置实体；hasWife(X,Y)是一个二元原子，表示实体变量X的妻子是实体变量Y。

在规则主体中，不同的原子是通过逻辑合取组合在一起的，且规则主体中的原子可以以肯定或者否定的形式出现，例如$$isFatherOf(X,Z)\leftarrow hasWife(X,Y)\wedge hasChild(Y,Z)\wedge \neg usedDivocied(X)\wedge \neg usedDivovied(Y)$$

• 霍恩规则：规则主体中只包含有肯定形式出现的原子而不包含否定形式出现的原子$$a_0\leftarrow a_1\wedge a_2\wedge a_3...\wedge a_n$$
• 路径规则：规则主体中的原子均为含有两个变量的二元原子，且规则主体的所有二元原子构成一个从规则头的两个实体之间的路径，且整个规则在知识图谱中构成一个闭环结构$$r_0(e_1,e_{n+1}\leftarrow r_1(e_1,e_2)\wedge r_2(e_2,e_3)\wedge ...\wedge r_n(e_n,e_{n+1})$$

规则的评估指标
支持度（support）	support(rule)	满足规则主体和规则头的实例个数
置信度（confidence）	confidence(rule) = $\frac{support(rule)}{\#body(rule)}$	置信度越高，规则质量也越高
基于部分完全假设的置信度（PCA confidence）	confidence(rule) = $\frac{support(rule)}{\#body(rule)\wedge r_0(x,y^{{}^{\prime }})}$	置信度越高，规则质量也越高
规则头覆盖度(head converage)	HC(rule) = $\frac{support(rule)}{\#head(rule)}$	规则的头覆盖度越高，规则质量也越高

• AMIE算法
  AMIE算法能挖掘的规则形如：$$fatherOf(f,c)\leftarrow motherOf(m,c)\wedge marriedTo(m,f)$$
  AMIE 定义了三个挖掘算子：

1. 增加悬挂原子:即在规则中增加一个原子，这个原子包含一个新的变量和一个已经在规则中出现的元素，可以是出现过的变量，也可以是出现过的实体
2. 增加实例化的原子：即在规则中增加一个原子，这个原子包含一个实例化的实体以及一个已经在规则中出现的元素
3. 增加闭合原子：即在规则中增加一个原子，这个原子包含的两个元素都是已经出现在规则中的变量或实体。增加闭合原子之后，规则就算构建完成了。

AMIE的两个用以缩小搜索空间的剪枝策略：

1. 设置最低规则头覆盖度过滤，头覆盖度很低的规则一般是一些边缘规则，可以直接过滤掉，在实践中，AMIE将头覆盖度值设为0.01
2. 在一条规则中，每在规则主体中增加一个原子，都应该使得规则的置信度增加，即$$confidence(a_0\leftarrow a_0\wedge a_2\wedge ...\wedge a_n\wedge a_{n+1})>confidence(a_0\leftarrow a_0\wedge a_2\wedge ...\wedge a_n)$$ 若不能提升规则整体置信度，则将拓展的规则剪枝掉。

参考

1. https://github.com/npubird/KnowledgeGraphCourse/blob/master/pub-14%E7%9F%A5%E8%AF%86%E6%8E%A8%E7%90%86.pdf
2. https://blog.csdn.net/pelhans/article/details/80091322