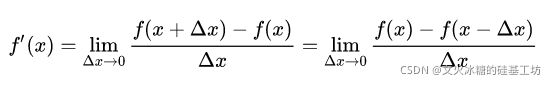[数值计算-19]：万能的任意函数的数值求导数方法

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120378620

---

目录

第1章 前言

第2章 导数的数值定义

第3章 导数的数值计算

3.1 定义支持任意一元函数的求导的函数

3.2 案例1：一元函数1

3.3 案例2：一元函数2

3.3 多元函数求偏导

---

---

---

第1章 前言

张量运算的前向运算与参数的自动反向求导都是深度学习最核心的基础。

前向运算其实直观，因为有前向运算的函数，一次带入函数的参数，就可以获得前向运算的数值。

如 loss =(f(x, w1, b1, w2, b2) - y) = (w2 * (w1 * x0 + b1) - b2 - y0) *2

在上述函数 中，假定（x0,y0)是一个已知的样本值，而w1,b1, w2, b2是自变量。

如果给定w1,b1, w2, b2的一个数值点(w1_0,b1_0, w2_0, b2_0))，很容易获得前向运算的值。

现在有一个问题：

（1）如何获得参数w1,b1, w2, b2在点点(w1_0,b1_0, w2_0, b2_0))的导数值呢？

（2）如果f()是任意的函数：自变量的个数任意，函数的表达式任意，如何获得每个参数在任意点处到偏导数呢？

（3）深度学习框架在反向求导的时候，为什么能够对任意loss函数进行反向求导呢？

（4）我们知道，如果获得某一函数的导函数的表达式，是很容易通过前向运算的方式，根据导函数获取计算出导数在任意一点的值，只就是某一函数在任意一点处的导数值，但如果无法获取导函数，有如何求导呢？

实际上，上述问题的核心是问题是：是否有一种简便的、万能的方法、进行数值求导？

答案是：有！

第2章 导数的数值定义

先回到导数的定义上，从中来发现解决问题的方法。

 上述表达是的核心思想是：要计算某一个点处的导数（斜率），可以用该点(x0,y0) 与一个与之极其相邻处的点(x0-p, f(x0-p) 这两个点斜率作为该点(x0,y0)的近似值。当p足够小时，近似度越高。

 这就是数值求导的核心思想。

第3章 导数的数值计算

3.1 定义支持任意一元函数的求导的函数

import numpy as np    
import math


#定义对任何函数
# 未优化函数：x+p, x
def approximate_derivative(func, x, p=1e-3):
    return ((func(x + p) - func(x)) / p)

# 优化后的函数：x+p，x-p
def approximate_derivative_opt(func, x, p=1e-3):
    return ((func(x + p) - func(x - p)) / (2*p))

其中, 影响求导精度最重要的参数就是p，即delta_x。

3.2 案例1：一元函数1

（0）定义一元函数1

# 原函数
def f1(x):
    return (x**2 + x**1 + 1)

# 导函数
def f1_derivative(x):
    return (2*x + 1)

（1）求样本点x=1.0处的导数

x = 1.0
p = 1e-6
f = f1

y_x = f(x)
deriv_x_p0 = f1_derivative(x)
deriv_x_p1 = approximate_derivative(f, x)
deriv_x_p2 = approximate_derivative(f, x, p)
deriv_x_p3 = approximate_derivative_opt(f, x, p)
print("前向运算值   =", y_x)
print("导函数求导p0 =", deriv_x_p0, "Error = ", deriv_x_p0 - deriv_x_p0)
print("反向导数值p1 =", deriv_x_p1, "Error = ", deriv_x_p1 - deriv_x_p0)
print("反向导数值p2 =", deriv_x_p2, "Error = ", deriv_x_p2 - deriv_x_p0)
print("反向导数值p3 =", deriv_x_p3, "Error = ", deriv_x_p3 - deriv_x_p0)

前向运算值   = 3.0
导函数求导p0 = 3.0 Error =  0.0
反向导数值p1 = 3.0009999999993653 Error =  0.0009999999993652864
反向导数值p2 = 3.000000999620056 Error =  9.99620056063577e-07
反向导数值p3 = 2.9999999999752447 Error =  -2.475530891388189e-11

备注：

• 优化后的数值求导approximate_derivative_opt()具有更高的精度
• 在数值求导公式不变的情况下，导数的精度与p的大小密切相关，p越小，精度越高

（2）求样本点x=2.0处的导数

x = 2.0
p = 1e-6
f = f1

y_x = f(x)
deriv_x_p0 = f1_derivative(x)
deriv_x_p1 = approximate_derivative(f, x)
deriv_x_p2 = approximate_derivative(f, x, p)
deriv_x_p3 = approximate_derivative_opt(f, x, p)
print("前向运算值   =", y_x)
print("导函数求导p0 =", deriv_x_p0, "Error = ", deriv_x_p0 - deriv_x_p0)
print("反向导数值p1 =", deriv_x_p1, "Error = ", deriv_x_p1 - deriv_x_p0)
print("反向导数值p2 =", deriv_x_p2, "Error = ", deriv_x_p2 - deriv_x_p0)
print("反向导数值p3 =", deriv_x_p3, "Error = ", deriv_x_p3 - deriv_x_p0)

前向运算值   = 7.0
导函数求导p0 = 5.0 Error =  0.0
反向导数值p1 = 5.001000000000033 Error =  0.0010000000000331966
反向导数值p2 = 5.00000100078779 Error =  1.0007877904172346e-06
反向导数值p3 = 5.000000000254801 Error =  2.5480062504357193e-10

3.3 案例2：一元函数2

（0）定义一元函数2

def f2(x):
    return (x**2 + x**1 + 1 + math.exp(x))

def f2_derivative(x):
    return (2*x + 1 + math.exp(x))

（1）求样本点x=1.0处的导数

x = 1.0
p = 1e-6
f = f2

y_x = f(x)
deriv_x_p0 = f2_derivative(x)
deriv_x_p1 = approximate_derivative(f, x)
deriv_x_p2 = approximate_derivative(f, x, p)
deriv_x_p3 = approximate_derivative_opt(f, x, p)
print("前向运算值   =", y_x)
print("导函数求导p0 =", deriv_x_p0, "Error = ", deriv_x_p0 - deriv_x_p0)
print("反向导数值p1 =", deriv_x_p1, "Error = ", deriv_x_p1 - deriv_x_p0)
print("反向导数值p2 =", deriv_x_p2, "Error = ", deriv_x_p2 - deriv_x_p0)
print("反向导数值p3 =", deriv_x_p3, "Error = ", deriv_x_p3 - deriv_x_p0)

前向运算值   = 5.718281828459045
导函数求导p0 = 5.718281828459045 Error =  0.0
反向导数值p1 = 5.720641422533035 Error =  0.0023595940739902233
反向导数值p2 = 5.71828418749476 Error =  2.359035715215896e-06
反向导数值p3 = 5.718281828492877 Error =  3.383249236321717e-11

（2）求样本点x=2.0处的导数

x = 2.0
p = 1e-6
f = f2

y_x = f(x)
deriv_x_p0 = f2_derivative(x)
deriv_x_p1 = approximate_derivative(f, x)
deriv_x_p2 = approximate_derivative(f, x, p)
deriv_x_p3 = approximate_derivative_opt(f, x, p)
print("前向运算值   =", y_x)
print("导函数求导p0 =", deriv_x_p0, "Error = ", deriv_x_p0 - deriv_x_p0)
print("反向导数值p1 =", deriv_x_p1, "Error = ", deriv_x_p1 - deriv_x_p0)
print("反向导数值p2 =", deriv_x_p2, "Error = ", deriv_x_p2 - deriv_x_p0)
print("反向导数值p3 =", deriv_x_p3, "Error = ", deriv_x_p3 - deriv_x_p0)

前向运算值   = 14.38905609893065
导函数求导p0 = 12.38905609893065 Error =  0.0
反向导数值p1 = 12.393751858796875 Error =  0.004695759866224947
反向导数值p2 = 12.389060794149032 Error =  4.695218381201016e-06
反向导数值p3 = 12.389056099237905 Error =  3.072546661542219e-10

3.3 多元函数求偏导

多元函数与一元函数求导的原理和本质是一样的，在具体实现上，就是定义任意参数的函数。

---

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/120378620