数值优化（Numerical Optimization）学习系列-计算导数（Calculating Derivatives）

概述

最优化问题中很多算法，包括非线性最优化、非线性等式等都需要计算导数。简单函数可以直接进行人工计算或者编码实现，对于复杂的情况，需要寻找一些方法进行计算或者近似。本节主要内容包括
1. 常见导数求解方法
2. 有限差分方法
3. 自动微分方法
4. 总结

常见导数求解方法

有限差分方法（Finite Differencing）

根据导数的定义，导数表示函数在给定点x处，给定无限小的涉动后函数值的改动。因此我们可以根据定义，在给定点x处给定一个无限小的抖动，看函数值的变化率，即

∂f∂xi≈f(x+ϵei)−f(x−ϵei)2ϵ

自动微分方法

基本思路就是将复杂的函数分解为基本函数以及基本运算，然后通过构建有向无环图进行求解。常见函数导数求解方法

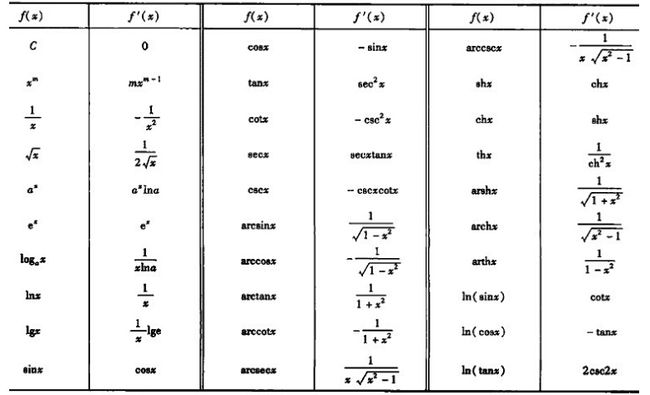
另外就是导数运算法则，例如函数加、减、乘除以及链式法则的应用。

符号微分法

有限微分近似算法

基础思想是泰勒定理和Lipschitz连续。介绍如下：
1. 泰勒公式：

f(x+p)=f(x)+∇f(x)Tp+12pT∇2f(x+tp)p

2. Lipschitz continuous: 对任意的x和x2

dY(f(x1,x2))≤KdX(x1,x2)

参考wiki

有限微分近似算法主要是基于导数定义，在给定点x处给定一个无限小的改动，看函数的变化。

前向微分

定义：

∂f(x)∂xi≈f(x+ϵei)−f(x)ϵ

对于n维的向量，需要计算量为（n+1）

方法推导

根据泰勒公式：

f(x+p)=f(x)+∇f(x)Tp+12pT∇2f(x+tp)p

假设 ||∇2f(x)||≤L ，L在一定范围内，则有

||f(x+p)−f(x)−∇f(x)Tp||≤(L/2)||p||2

，此时令 p=ϵei ，代入可以得到

∂f(x)∂xi≈f(x+ϵei)−f(x)ϵ+δ ;δ≤(L/2)ϵ

可见误差和无限小的改动相关。

在用计算机解决问题时，需要注意的是计算机浮点数本身就会有误差，例如对于double类型，该误差为u=1.1*10^(-16)。此时 ϵ=u√ 会得到最优的结果

中心微分方法

定义

∂f∂xi≈f(x+ϵei)−f(x−ϵei)2ϵ

对于N维向量，需要进行(2N+1)次运算

方法推导

该方法的基础就是函数必须能保证二级导数存在并且满足Lipschitz连续，此时根据泰勒公式

f(x+p)=f(x)+∇f(x)Tp+12pT∇2f(x+tp)p

变换后有

f(x+p)=f(x)+∇f(x)Tp+12pT∇2f(x)p+O(||p||3)

代入 p=ϵei和p=−ϵei ，可以得到

f(x+ϵei)=f(x)+ϵ∂f(x)∂xi+12ϵ2∂2f∂x2i+O(||ϵ||3)

f(x−ϵei)=f(x)−ϵ∂f(x)∂xi+12ϵ2∂2f∂x2i+O(||ϵ||3)

两个等式相减，同时两端同时除以 ϵ 可以得到

∂f∂xi≈f(x+ϵei)−f(x−ϵei)2ϵ+O(ϵ2)

可见相比于前向微分，它的误差变成 O(ϵ2) 。考虑到计算机的精度问题，参数 ϵ=u1/3 最优。

应用

雅克比矩阵（Jacobian）

定义，对于函数向量r: Rn→Rm ，雅克比矩阵就是每一个函数对x求导得到的矩阵

J(x)=⎡⎣⎢⎢⎢⎢⎢∇r1(x)T∇r2(x)T...∇rm(x)T⎤⎦⎥⎥⎥⎥⎥

根据有限微分的定义可以扩展到函数向量上

∂r(x)∂xi≈r(x+ϵei)−r(x)ϵ

此时计算一次可以得到矩阵的一列。
对于某些稀疏的矩阵，可以将不相交的变量进行分类，一次计算可以得到多列。

Hessian矩阵

Hessian矩阵是对称的，如果按照优先微分的方法得到的Hessian矩阵可能不是对称的，可以通过对称位置取平均的方法。
对于很多重要的算法，需要求解的是Hessian和某向量的乘积，根据泰勒公式有

∇f(x+ϵp)=∇f(x)+ϵ∇2f(x)Tp+O(||ϵ||3)

，从而有

∇2f(x)Tp≈∇f(x+ϵp)−∇f(x)ϵ

，由于一阶导数可以得到，因此可以计算得到Hessian和某向量的乘积。

如果需要计算Hessian矩阵本身，则根据

f(x+p)=f(x)+∇f(x)Tp+12pT∇2f(x)p+O(||p||3)

代入 p=ϵei ;p=ϵej ;p=ϵ(ei+ej) 推导可以得到

∂2f∂xi∂xj≈f(x+ϵei+ϵej)−f(x−ϵei)−f(x−ϵej)−f(x)ϵ2+O(ϵ)

对于稀疏的Hessian矩阵，可以利用Hessian对称原理得到高效算法。

自动微分方法

根据前面的介绍，自动微分方法的主要思路是将复杂函数分解成简单函数的简单运算，然后合成最终的结果。主要有前向模式和后向模式，分别介绍如下。
在进行算法之前，一般需要将复杂函数表示成简单函数以及运算的有向无环图，例如： f(x)=(x1x2sinx3+ex1x2)/x3 ，可以表示为

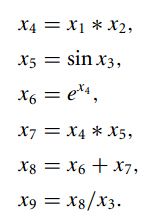
图示为

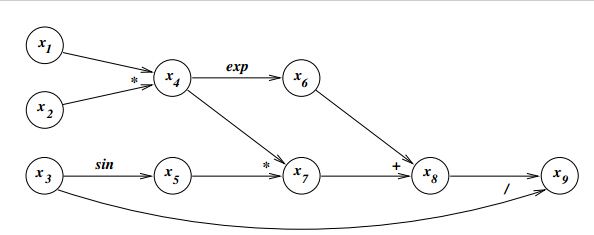
在实际应用中不需要人工构建该图。

前向模式

从前向后依次计算各个节点对目标节点的导数，思路是链式规则。
例如

∇x7=∂x7∂x4∇x4+∂x7∂x5∇x5

如果计算了所有的 ∇xi 则最终的结果 ∇x9

后向模式

和前向模式相反，根据节点的孩子节点计算得到该节点的导数，BP算法和图置信传播都是利用该思想。

∂f∂xi=∑j a child ofi∂f∂xj∂xj∂xi

对比

1. 对于结果是实数的函数，即 f:Rn→R ，此时后向方式效率更高，对于函数向量，即 f:Rn→Rm ，两者效率差不多
2. 对于存储空间，后向模式需要保存所有的中间导数结果，可以通过一些优化算法进行优化，例如check pointing

总结

通过该小结的学习，可以了解到
1. 常见计算导数的方法
2. 有限微分原理和可选方法
3. 自动微分原理和可选方法
4. 应用到计算梯度、雅克比矩阵或者Hessian矩阵，以及稀疏情况下如何优化。