【啃书】《深度学习入门 基于Python的理论与实现》第3章 神经网络

神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。

3.1 从感知机到神经网络

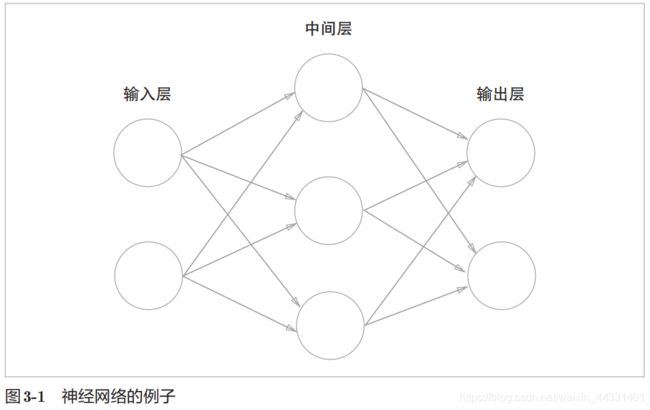
激活函数（activation function）的作用在于决定如何来激活输入信号的总和。

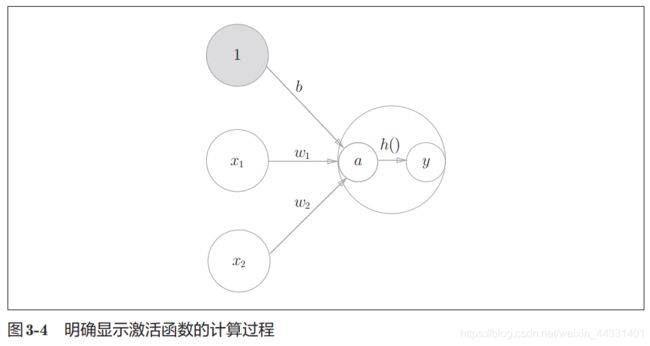
3.2 激活函数

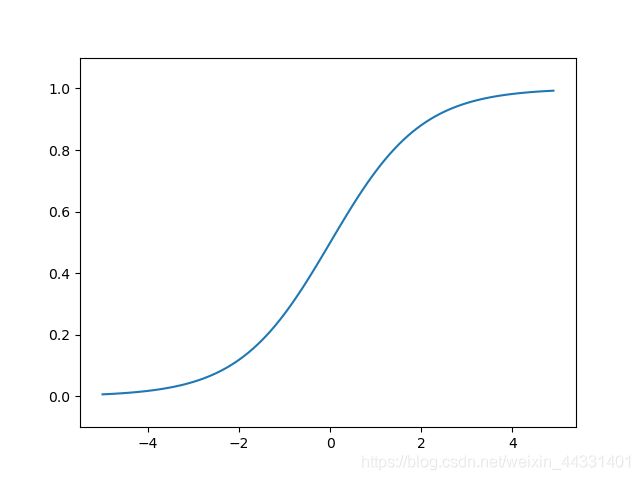
神经网络中经常使用的一个激活函数就是式（3.6）表示的sigmoid函数（sigmoid function）

import numpy as np
import matplotlib.pylab as plt
def step_function(x):
    return np.array(x > 0, dtype=np.int)

def sigmoid(x):
    return 1 / (1 + np.exp(-x))


x = np.arange(-5.0, 5.0, 0.1)
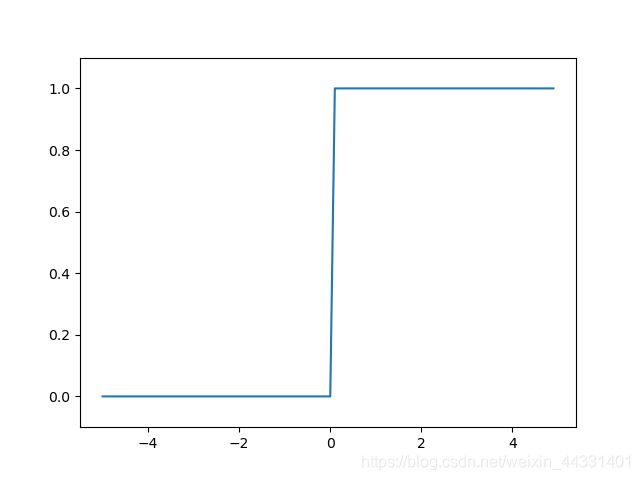
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()


x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()

阶跃函数图形

sigmoid函数图形

ReLU（Rectified Linear Unit）函数在输入大于0时，直接输出该值；在输入小于等于0时，输出0。ReLU函数可以表示为下面的式(3.7)。


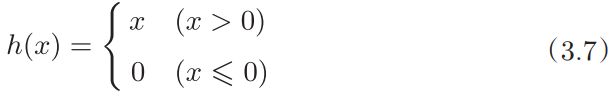
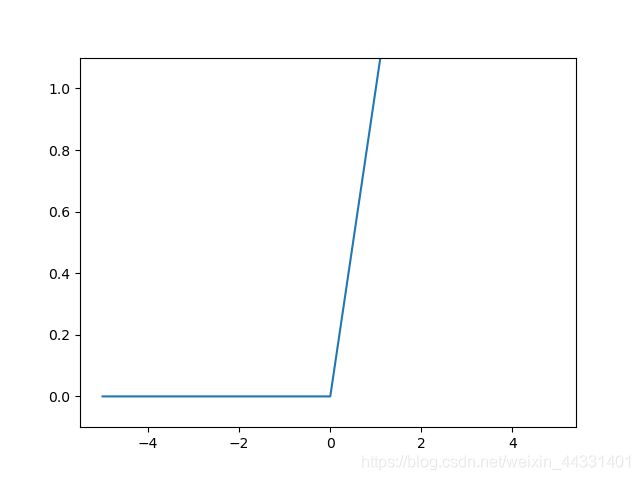
ReLU函数图形

3.4 3层神经网络的实现

# 通过巧妙地使用NumPy多维数组，我们高效地实现了神经网络。
import numpy as np
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
def identity_function(x):
    return x

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])    
    network['b3'] = np.array([0.1, 0.2])
    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)
    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [ 0.31682708 0.69627909]

3.5 输出层的设计

神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出层的激活函数。一般而言，回归问题用恒等函数，分类问题用softmax函数。
分类问题中使用的softmax函数可以用下面的式（3.10）表示。

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c) # 溢出对策
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

本章所学的内容

• 神经网络中的激活函数使用平滑变化的sigmoid函数或ReLU函数。
• 通过巧妙地使用NumPy多维数组，可以高效地实现神经网络。
• 机器学习的问题大体上可以分为回归问题和分类问题。
• 关于输出层的激活函数，回归问题中一般用恒等函数，分类问题中一般用softmax函数。
• 分类问题中，输出层的神经元的数量设置为要分类的类别数。
• 输入数据的集合称为批。通过以批为单位进行推理处理，能够实现高速的运算。

系列文章：
【啃书】《深度学习入门 基于Python的理论与实现》第1章 Python入门
【啃书】《深度学习入门 基于Python的理论与实现》第2章 感知机

中 深度学习入门 基于Python的理论与实现 原作名- Deep Learning from Scratch[文字版][[日]斋藤康毅[译] 陆宇杰][人民邮电出版社][2018-7][9787115485588]