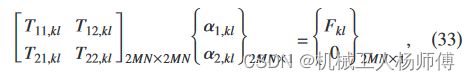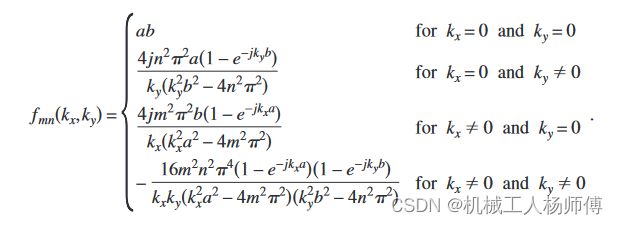固支双层板隔声量Matlab实现(Xin Fengxian老师论文复现)
1.复现文献
[1] Xin FX, Lu TJ. Analytical and experimental investigation on transmission loss of clamped double panels: Implication of boundary effects. Journal of the Acoustical Society of America, 2009, 125 (3): 1506-1517.
[2] Xin, F. X., Lu, T. J., & Chen, C. Q. (2008). Vibroacoustic behavior of clamp mounted double-panel partition with enclosure air cavity. The Journal of the Acoustical Society of America, 124(6), 3604–3612. doi:10.1121/1.3006956
整个Matlab复现过程需要对两篇文献的理论内容结合,求解模态位移系数矩阵![]() 主要参考文章[1],通过模态位移系数矩阵
主要参考文章[1],通过模态位移系数矩阵![]() 求解隔声量主要参考文章[2]。
求解隔声量主要参考文章[2]。
2.复现思路
(1) 核心公式为[1]中的式(33)
式中T矩阵和F矩阵为已知矩阵,通过F矩阵左乘T矩阵的逆可以求解![]() 矩阵
矩阵
![]()
(2) 通过模态位移系数矩阵![]() ,根据文章[2]中
,根据文章[2]中![]() 和
和![]() 的详细定义,求解隔声量;
的详细定义,求解隔声量;
3.Matlab实现
3.1计算分析及子函数划分
T矩阵的计算需要delta11、delta12、delta13、delta21、delta22、delta23、delta24;且delta算子是和频率无关的量;可以放在循环外面进行预处理,而T矩阵的计算则是与频率相关,需放在频率循环遍历里面;
[delta11,delta12,delta13,delta21,delta22,delta23,delta24] = GetDelta(a,b,M,N)[T11,T12,T21,T22] = GetT(D1,D2,a,b,m1,m2,H,w,j,kz,rho0,delta11,delta12,delta13,delta21,delta22,delta23,delta24) F矩阵需要计算出![]() 同时需要对应分类,所以构建两个子函数;
同时需要对应分类,所以构建两个子函数;
[Fkl,F] = GetFkl(kx,ky,a,b,j,w,rho0,I,M,N)fx = GetFx(kx,ky,a,b,j,m,n)TL隔声量计算[2]
3.2 delta算子子函数
function [delta11,delta12,delta13,delta21,delta22,delta23,delta24] = GetDelta(a,b,M,N)
%% delta11,delta12求解
delta11 = [];
delta12 = [];
diagone = ones(M,N)-diag(ones(M,1),0);
for n = 1:1:N
for m = 1:1:M
lamdars1 = 3*((m/a)^4)+3*((n/b)^4)+2*((m/a)^2)*((n/b)^2); %lamdars1计算出来是数值
delta11 = [delta11,lamdars1];
end
lamdars2 = (2*(n^4)/(b^4)).*diagone; %lamdars2计算出来是一个M*N的矩阵
delta12 = blkdiag(delta12,lamdars2);
end
delta11 = diag(delta11,0);
%% delta13求解
lamda13 = (zeros(M,N)+diag(ones(M,1),0));
for i = 1:1:M
lamda13(i,i) = (2/(a^4))*(i^4);
end
delta13 = GenerateDiag(lamda13,M,N,1);
%% delta21求解
delta21 = (9*a*b/4)*diag(ones(M*N,1),0);
%% delta22求解
lamda22 = (3*a*b/2).*diagone;
delta22 = GenerateDiag(lamda22,M,N,2);
%% delta23求解
lamda23 = (3*a*b/2).*diag(ones(M,1),0);
delta23 = GenerateDiag(lamda23,M,N,1);
%% delta24求解
lamda24 = (a*b).*diagone;
delta24 = GenerateDiag(lamda24,M,N,1);
end在计算delta过程中常需要用矩阵生成对角阵,此功能写成子函数
function delta = GenerateDiag(lamda,M,N,flag)
%% 构建以为同维度0矩阵对角元素、以目标矩阵为其他元素的对角阵
if flag==1
tempx = [];
tempy = [];
tempz = [];
%构建出全为lamda的矩阵
for i = 1:1:M
tempx = [tempx lamda];
end
for j = 1:1:N
tempy = [tempy;tempx];
end
%构建出以lamda为对角的矩阵
for i = 1:1:M
tempz = blkdiag(tempz,lamda);
end
%做差得到结果
delta = tempy-tempz;
%% 构建以相同目标矩阵为对角元素、以同维度0矩阵为其他元素的对角阵(其中输入lamda为目标矩阵).0
elseif flag==2
delta = [];
for i = 1:1:M
delta = blkdiag(delta,lamda);
end
%% flag标志位异常,抛出错误
else
error('flag标志位异常!')
end
end3.3 T矩阵子函数
function [T11,T12,T21,T22] = GetT(D1,D2,a,b,m1,m2,H,w,j,kz,rho0,delta11,delta12,delta13,delta21,delta22,delta23,delta24)
delta1 = delta11+delta12+delta13;
delta2 = delta21+delta22+delta23+delta24;
fe = exp(j*kz*H);
f2e = exp(2*j*kz*H);
T11 = 4*D1*pi^4*a*b*delta1-(m1*w^2+j*w*rho0*2*w*f2e/(kz*(1-f2e)))*delta2;
T12 = (j*w*rho0*2*w*fe/(kz*(1-f2e)))*delta2;
T21 = (j*w*rho0*2*w*fe/(kz*(1-f2e)))*delta2;
T22 = 4*D2*pi^4*a*b*delta1-(m2*w^2+j*w*rho0*2*w*f2e/(kz*(1-f2e)))*delta2;
end3.4 F矩阵
function [Fkl,F] = GetFkl(kx,ky,a,b,j,w,rho0,I,M,N)
Fkl = zeros(M*N,1);
i = 1;
for n = 1:1:N
for m = 1:1:M
Fkl(i,1) = 2*j*w*rho0*I*GetFx(kx,ky,a,b,j,m,n);
i = i+1;
end
end
F = [Fkl;zeros(M*N,1)];
end其中Fx分类讨论情况写成子函数
function fx = GetFx(kx,ky,a,b,j,m,n)
if kx==0&&ky==0
fx = a*b;
elseif kx==0&&ky~=0
fx = (4*j*n^2*pi^2*a*(1-exp(-j*ky*b)))/(ky*(ky^2*b^2-4*n^2*pi^2));
elseif kx~=0&&ky==0
fx = (4*j*m^2*pi^2*b*(1-exp(-j*kx*a)))/(kx*(kx^2*a^2-4*m^2*pi^2));
elseif kx~=0&&ky~=0
fx = -(16*m^2*n^2*pi^4*(1-exp(-j*ky*b))*(1-exp(-j*kx*a)))/(kx*ky*(ky^2*b^2-4*n^2*pi^2)*(kx^2*a^2-4*m^2*pi^2));
else
error('kx、ky错误');
end3.5 TL隔声量计算
function TL = GetTL(alpha1,alpha2,rho0,w,c0,I,kx,ky,kz,a,b,M,N,j)
%alpha由MN*1重排为M*N;为了(m,n)能直接取到对应元素
alpha1 = reshape(alpha1,[M,N]);
alpha2 = reshape(alpha2,[M,N]);
K = M;
L = N;
Sum11 = 0;%算子11
Sum12 = 0;%算子12
Sum13 = 0;%算子13
Sum22 = 0;%算子22
for m = 1:1:M
for n = 1:1:N
if kx==0&&ky==0
Sum11 = a*b;
Sum12 = Sum12+alpha1(m,n)*a*b;
elseif kx==0&&ky~=0
Sum11 = j*a*(-1+exp(-2*j*ky*b))/(2*ky);
Sum12 = Sum12+alpha1(m,n)*4*j*n^2*pi^2*a*(1-exp(-j*ky*b))/(ky*(ky^2*b^2-4*n^2*pi^2));
elseif kx~=0&&ky==0
Sum11 = j*b*(-1+exp(-2*j*kx*a))/(2*kx);
Sum12 = Sum12+alpha1(m,n)*4*j*m^2*pi^2*b*(1-exp(-j*kx*a))/(kx*(kx^2*a^2-4*m^2*pi^2));
elseif kx~=0&&ky~=0
Sum11 = -(1-exp(-2*j*kx*a)-exp(-2*j*ky*b)+exp(-2*j*(kx*a+ky*b)))/(4*kx*ky);
Sum12 = Sum12+alpha1(m,n)*16*(-1)*m^2*n^2*pi^4*(1-exp(-j*ky*b)*(1-exp(-j*kx*a)))/(kx*ky*(kx^2*a^2-4*m^2*pi^2)*(ky^2*b^2-4*n^2*pi^2));
end
for k = 1:1:K
for i = 1:1:L
if m==k&&n==i
Sum13 = Sum13+alpha1(m,n)*alpha1(k,i)*(9*a*b/4);
Sum22 = Sum22+alpha2(m,n)*alpha2(k,i)*(9*a*b/4);
elseif m==k&&n~=i
Sum13 = Sum13+alpha1(m,n)*alpha1(k,i)*(3*a*b/2);
Sum22 = Sum22+alpha2(m,n)*alpha2(k,i)*(3*a*b/2);
elseif m~=k&&n==i
Sum13 = Sum13+alpha1(m,n)*alpha1(k,i)*(3*a*b/2);
Sum22 = Sum22+alpha2(m,n)*alpha2(k,i)*(3*a*b/2);
elseif m~=k&&n~=i
Sum13 = Sum13+alpha1(m,n)*alpha1(k,i)*(a*b);
Sum22= Sum22+alpha2(m,n)*alpha2(k,i)*(a*b);
end
end
end
end
end
Win =(rho0*w^2/(2*c0))*abs(4*I^2*Sum11-(4*I*w/kz)*Sum12+(w/kz)^2*Sum13);
Wr = (rho0*w^2/(2*c0))*abs((w/kz)^2*Sum22);
TL = 10*log10(Win/Wr);
end3.6 主函数及主要参数的定义
function Xin20082009DoublePlate()
j = sqrt(-1);
Freq=zeros(10000,1); %预分配内存
TL=zeros(10000,1); %预分配内存
bar= waitbar(0,'Simulation inprocess');%利用waitbar函数显示循环进度
%% 空气参数定义
rho0 = 1.21;%空气密度
c0 = 343;%空气声速
I0 = 1;%入射声波幅值Pa
H = 0.08;%空气层厚度
phi = 0;%入射角
theta = 0;%方位角
%% 平板参数定义
a = 1;%x方向板长
b = 1;%y方向板长
h1 = 0.005;%入射侧板厚
h2 = 0.005;%透射侧板厚
rho = 2700;%板密度
E = 70e9;%板杨氏模量
v = 0.33;%板泊松比
eta = 0.01;%板耗散系数
m1 = rho*h1;%入射侧板面密度
m2 = rho*h2;%透射侧板面密度
D1 = E*(1+j*eta)*h1^3/(12*(1-v^2));%入射侧板弯曲刚度
D2 = E*(1+j*eta)*h2^3/(12*(1-v^2));%透射侧板弯曲刚度
%% 模态截断阶数
M = 10;
N = 10;
%% 求解delta算子
[delta11,delta12,delta13,delta21,delta22,delta23,delta24] = GetDelta(a,b,M,N);
%% 隔声系数计算
fmin = 1;%计算下限
fmax = 10000;%计算上限
df = 1;%循环步进长度
for f = fmin:df:fmax
s=['Simulation in process:' num2str(ceil((f-fmin)*100/(fmax-fmin))) '%'];%进度显示框中的字符串
waitbar((f-fmin)/(fmax-fmin),bar,s);%进度显示
w = 2*pi*f;%角频率
k0 = w/c0;
kx = k0*sin(phi)*cos(theta);
ky = k0*sin(phi)*sin(theta);
kz = k0*cos(phi);
%% 求解T矩阵
[T11,T12,T21,T22] = GetT(D1,D2,a,b,m1,m2,H,w,j,kz,rho0,delta11,delta12,delta13,delta21,delta22,delta23,delta24);
T = [T11 T12;T21 T22];
%% 求解F、alpha(alpha1、alpha2)
[Fkl,F] = GetFkl(kx,ky,a,b,j,w,rho0,I0,M,N);
alpha = T\F;
alpha1 = alpha(1:M*N,:);
alpha2 = alpha(M*N+1:end,:);
%% 求解隔声量TL
TL(f) = GetTL(alpha1,alpha2,rho0,w,c0,I0,kx,ky,kz,a,b,M,N,j);
Freq(f) = f;
end
semilogx(Freq,TL);
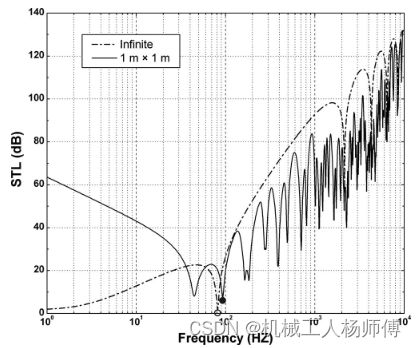
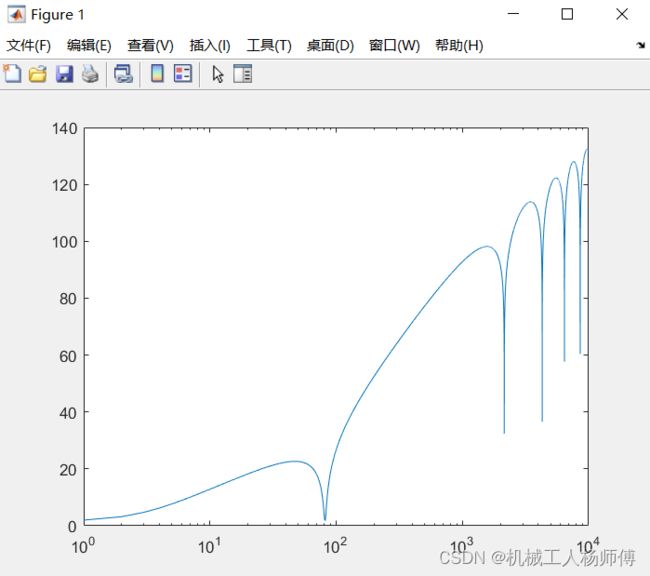
end4.仿真结果
将各子函数构建好,调用主子函数即可。
Xin20082009DoublePlate();(左图:a=1,b=1)(右图:a=1e8,b=1e8)