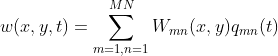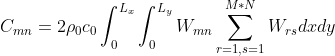薄膜声学超材料模态叠加法Matlab实现(Zhang Yuguang论文复现)

1.理论分析

        设超材料的一个周期单元的长度为Lx、Ly；薄膜密度为，薄膜张紧力为T；振子尺寸为lx、ly，振子密度为，振子位置为；板的横向位移为w

        定义m、n分别为x、y方向的模态数，模态型函数为：

        列出声波入射在板上引起的振动微分方程

其中为空气密度，为入射声波幅值；

        根据振动微分方程求解得到以下等式

各矩阵的求解方式如下：

 

 

 

        求解得模态位移系数

         透射系数

        隔声量

---

2.Matlab实现

        2.1构建M、C矩阵

        M、C矩阵形式类似，故采用同一个子函数计算

function [Mmn,Cmn] = GenerateMC(M,N,Lx,Ly,rhos,rho0,c0)
Mmn = [];
Cmn = [];
TempM = 0;    
TempC = 0;
for m = 1:M
    for n = 1:N
        for r = 1:M
            for s = 1:N
                 fun = @(x,y) sin(m.*pi.*x./Lx).*sin(n.*pi.*y./Ly).*sin(r.*pi.*x./Lx).*sin(s.*pi.*y./Ly);
                 Temp = integral2(fun,0,Lx,0,Ly);
                 TempM = TempM+rhos*Temp;
                 TempC = TempC+2*rho0*c0*Temp;
            end
        end
        Mmn = blkdiag(Mmn,TempM);
        Cmn = blkdiag(Cmn,TempC);
        TempM = 0;    
        TempC = 0;
    end
end
end

        2.2构建K矩阵

function Kmn = GenerateK(M,N,Lx,Ly,T)
Kmn = [];
TempK = 0;
for m = 1:M
    for n = 1:N
        for r = 1:M
            for s = 1:N
                 fun = @(x,y) T*((r*pi/Lx)^2+(s*pi/Ly)^2)*sin(m.*pi.*x./Lx).*sin(n.*pi.*y./Ly).*sin(r.*pi.*x./Lx).*sin(s.*pi.*y./Ly);
                 Temp = integral2(fun,0,Lx,0,Ly);
                 TempK = TempK+Temp;
            end
        end
        Kmn = blkdiag(Kmn,TempK);
        TempK = 0;
    end
end
end

        2.3构建H矩阵

function Hmn = GenerateH(M,N,Lx,Ly)
Hmn = zeros(M*N,1);
k = 1;
for m = 1:M
    for n = 1:N
        fun = @(x,y) sin(m.*pi.*x./Lx).*sin(n.*pi.*y./Ly);
        Hmn(k,1) = integral2(fun,0,Lx,0,Ly);
        k = k+1;
    end
end
end

        2.4构建Q矩阵

function Qmn = GenerateQ(M,N,Lx,Ly,rhomass,x0,y0,lx,ly)
k = 1;
Qmn = zeros(M*N,M*N);
for m = 1:M
    for n = 1:N
        for r = 1:M
            for s = 1:N
                fun = @(x,y) sin(m.*pi.*x./Lx).*sin(n.*pi.*y./Ly).*sin(r.*pi.*x./Lx).*sin(s.*pi.*y./Ly);
                if mod(k,M*N)==0
                    Qmn(floor(k/(M*N)),9) = rhomass*integral2(fun,x0,x0+lx,y0,y0+ly);
                else
                    Qmn(floor(k/(M*N))+1,mod(k,M*N)) = rhomass*integral2(fun,x0,x0+lx,y0,y0+ly);
                end
                k = k+1;
            end
        end
    end
end
end

        2.5主子函数

function MembraneMetamaterialPlate()
STL = zeros(10000,1);
F = zeros(10000,1);
%% 参数定义
j = sqrt(-1);
rho0 = 1.21;%空气密度
c0 = 343;%空气声速
rhos = 0.0912;%薄膜面密度
T = 487.4;%薄膜张力
Lx = 0.0274;%薄膜x方向尺寸
Ly = 0.0274;%薄膜y方向尺寸
m = 0.00032;%质量块质量，单位是kg
r = 0.00193;%质量块半径
lx = sqrt(pi*r^2);%质量块x方向尺寸
ly = sqrt(pi*r^2);%质量块y方向尺寸
x0 = (Lx-lx)/2;%质量块左下角位置x方向
y0 = (Ly-ly)/2;%质量块左下角位置y方向
rhomass = m/(lx*ly);%质量块面密度
M = 3;%x方向模态数
N = 3;%y方向模态数
%% 生成M、I、C、K、H矩阵
[Mmn,Cmn] = GenerateMC(M,N,Lx,Ly,rhos,rho0,c0);
Kmn = GenerateK(M,N,Lx,Ly,T);
Hmn = GenerateH(M,N,Lx,Ly);
Qmn = GenerateQ(M,N,Lx,Ly,rhomass,x0,y0,lx,ly);
for f = 1:10000
    w = 2*pi*f;
    tp = abs((2*rho0*c0*w/(Lx*Ly))*Hmn'*(((j*w^2*(Mmn+Qmn))+w*Cmn-j*Kmn)\(Hmn)));
    STL(f) = 20*log10(1/tp);
    F(f) = f;
end
semilogx(F,STL);
xlim([100,7000]);
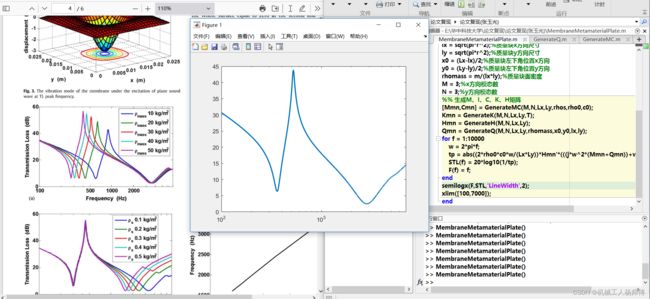
end

        2.6仿真结果

---

3.论文中需要注意的地方

         其博士论文中这个地方的表达式存在错误，二重积分式只有子啊r==n且s==m时才有值，其他情况下均约等于0；

4.复现文献

[1]张玉光. 薄膜型声学超材料隔声特性研究[D].国防科学技术大学,2014.

[1]Yuguang, Zhang, and, et al. Theoretical investigation of the sound attenuation of membrane-type acoustic metamaterials[J]. Physics Letters A, 2012.