深度学习基础——week4
更好的阅读体验!!
序列模型
例子
音乐、语言、文本、视频、股价…
统计方法
方案A:马尔科夫假设
假设当前当前数据只跟 τ \tau τ 个过去数据点相关
p ( x t ∣ x 1 , … x t − 1 ) = p ( x t ∣ x t − τ , … x t − 1 ) = p ( x t ∣ f ( x t − τ , … x t − 1 ) ) p\left(x_{t} \mid x_{1}, \ldots x_{t-1}\right)=p\left(x_{t} \mid x_{t-\tau}, \ldots x_{t-1}\right)=p\left(x_{t} \mid f\left(x_{t-\tau}, \ldots x_{t-1}\right)\right) p(xt∣x1,…xt−1)=p(xt∣xt−τ,…xt−1)=p(xt∣f(xt−τ,…xt−1))
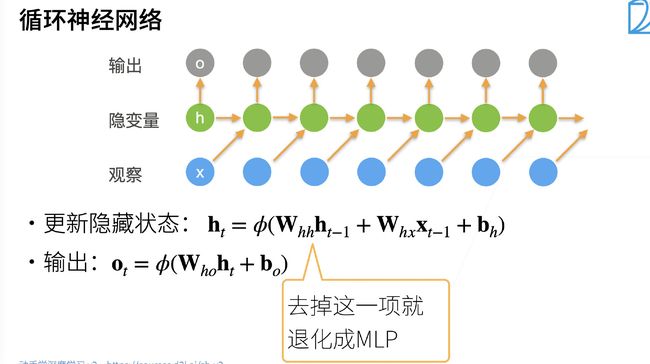
方案B:潜变量模型
- 引人潜变量 h t h_{t} ht 来表示过去信息 h t = f ( x 1 , … x t − 1 ) h_{t}=f\left(x_{1}, \ldots x_{t-1}\right) ht=f(x1,…xt−1)
- 这样 x t = p ( x t ∣ h t ) x_{t}=p\left(x_{t} \mid h_{t}\right) xt=p(xt∣ht)
文本预处理
- 序列数据往往存在多种形式,文本是其中常见的形式之一,例如一篇文章可以被简单地看作是一串单词序列,甚至是一串字符序列
- 将文本当做时序序列,将文本中的字或者字符、词当成样本,样本之间是存在时序信息的,因此文本是一个很长的时序序列
- 文本预处理的核心思想是如何将文本中的词转化成能够训练的样本
常见的文本预处理步骤
1、读取数据集:将文本作为字符串加载到内存中
- 将数据集读取到由多条文本行组成的列表中,其中每一条文本行都是一个字符串
- 将非大小写字符全部变成空格(这虽然是一种有损的操作,但是能够使后续的操作变得更加简单)
- 去掉回车
- 将所有字母全部变成小写
2、词元化:将字符串拆分为词元(如单词和字符)
- tokenize 是 NLP 中一个比较常见的操作:将一个句子或者是一段文字转化成 token(字符串、字符或者是词)
- 将文本行列表( lines )作为输入,列表中的每个元素都是一个文本序列(比如一条文本行)
- 将每个文本序列拆分成一个词元列表,词元( token,英文中 token 一般有两种表示单元:一种是一个词作为一个基本单元,词相对来说,会让机器学习的模型更简单一点;一种是一个字符串作为一个基本单元,好处是样本数量比较少,坏处是还需要学习字符串的构成,字符串是如何由词构成的)是文本的基本单位
- 中文的话会有所不同,因为在中文的段落中,词与词之间的间隔不是使用空格来进行间隔的,所以在中文中如果想使用词来表示 token 的话,还需要对其进行分词,分词相对来讲不是很容易
- 通过拆分,文本序列就被拆分成了许多 token 列表,这些列表要么是空,要么是有许多 token 在其中
- 最后返回一个由词元列表组成的列表,其中每个词元都是一个字符串( string )
3、建立词表,将拆分的词元映射到数字索引:将文本转换为数字索引序列,方便模型操作
- 词元的类型是字符串,而模型需要的输入是数字(模型训练使用的都是 tensor ,而 tensor 都是基于下标的),因此这种类型不方便模型使用,所以需要构建一个字典,通常也叫做词汇表(vocabulary),用来将字符串类型的 token (要么是 word ,要么是 char )映射到从 0 开始的数字索引中
- 首先将训练集中所有的文档合并到一起,然后对它们的唯一词元进行统计,得到最终的统计结果 – 语料( corpus )
然后根据每个唯一词元的出现频率,为其分配一个数字索引,对于出现次数较少的词元,通常会被移除,以降低复杂性(min_freq:在 NLP 中,有很多词是不出现的,如果使用词的话,这些词可能在文本中就出现了几次,在这种情况下如果要进行训练的话可能比较困难,这里的 min_freq 指的是一个 token 在文本序列中出现的最少次数,如果少于这个数字的话,会将这些出现频率较低的 token 全部视为 “unknown”) - 语料库中不存在或者是已删除的任何词元都将映射到一个特定的未知词元 “”
- 还可以选择增加一个列表,用于保存保留下来的词元,比如填充词元( “” );序列开始词元( “” );序列结束词元( “” )
小结
- 将文本作为字符串加载到内存中
- 将字符串拆分为词元(如单词和字符)
- 建立一个词表,将拆分的词元映射到数字索引
- 将文本转换为数字索引序列,方便模型操作
语言模型
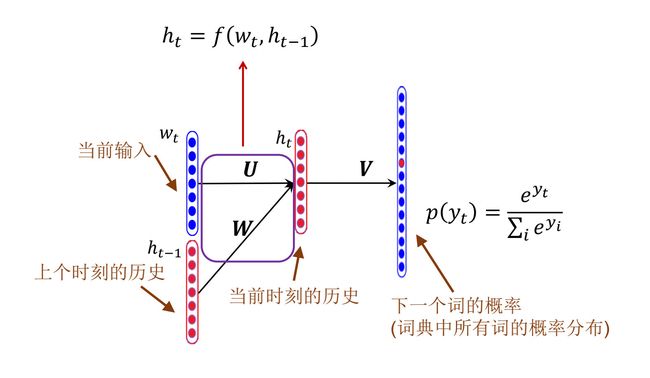
定义
给定文本序列 x 1 , … , x T x_{1}, \ldots, x_{T} x1,…,xT, 语言模型的目标是估计联合概率 p ( x 1 , … , x T ) p\left(x_{1}, \ldots, x_{T}\right) p(x1,…,xT)
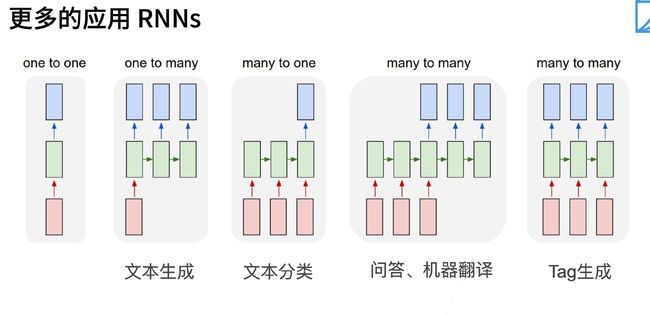
应用
- 做预训练模型 (eg BERT, GPT-3)
- 生成本文, 给定前面几个词, 不断的使用 x t ∼ p ( x t ∣ x 1 , … , x t − 1 ) x_{t} \sim p\left(x_{t} \mid x_{1}, \ldots, x_{t-1}\right) xt∼p(xt∣x1,…,xt−1) 来 生成后续文本
马尔可夫模型与 n n n元语法
如果 P ( x t + 1 ∣ x t , … , x 1 ) = P ( x t + 1 ∣ x t ) P(x_{t+1} \mid x_t, \ldots, x_1) = P(x_{t+1} \mid x_t) P(xt+1∣xt,…,x1)=P(xt+1∣xt),
则序列上的分布满足一阶马尔可夫性质。
阶数越高,对应的依赖关系就越长。
这种性质推导出了许多可以应用于序列建模的近似公式:
$$
\begin{aligned}
P(x_1, x_2, x_3, x_4) &= P(x_1) P(x_2) P(x_3) P(x_4),\
P(x_1, x_2, x_3, x_4) &= P(x_1) P(x_2 \mid x_1) P(x_3 \mid x_2) P(x_4 \mid x_3),\
P(x_1, x_2, x_3, x_4) &= P(x_1) P(x_2 \mid x_1) P(x_3 \mid x_1, x_2) P(x_4 \mid x_2, x_3).
\end{aligned}
$$
通常,涉及一个、两个和三个变量的概率公式分别被称为
“一元语法”(unigram)、“二元语法”(bigram)和“三元语法”(trigram)模型。