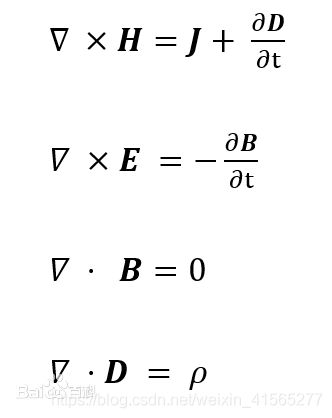电磁场与电磁波第二章笔记——静场 麦克斯韦方程组
- 电流密度
微观上,![]() v :带电粒子漂移速度。
v :带电粒子漂移速度。
- 电荷守恒定律:
单位时间内流入孤立系统边界的电荷量等于该孤立系统单位时间的电荷增量。
又称电流连续性方程。
- 静电场性质
(1)库仑定律
满足线性叠加定理
- 电场和电场强度
- 静电场的特性
①有散场。散度源是电荷——静电场高斯定理;
高斯定理积分形式:闭合面的电场通量等于此闭合面内包围的电荷量的和(常数因子)
表明静电场的力线发源于正电荷,终止于负电荷,没有电荷的位置力线连续。
②无旋场
③力和能量属性
- 一些典型的电场
点电荷的:与距离平方反比,球面等电位。
无限大均匀带电平面:与带电平面垂直,是匀强场,即与到该面的距离无关。
无限长均匀带电线:垂直电线指向(或远离)场点,与距离反比。
静电场是电荷之间,静磁场是电流元之间。
- 磁场基本性质
- 无散。磁通连续性定理/磁场高斯定理
- 有旋。安培环路定理
表述:磁感应强度沿任何闭合环路L的线积分,等于穿过这环路所有电流强度的代数和的![]() 倍。(真空)
倍。(真空)
典型磁场——无限长圆柱线电流:圆柱电流内部,随半径增加,磁场线性增强;外部则反比。
- 位移电流:电位移矢量的变化率,和传导电流一起构成全电流。位移电流的引入解决了时变电磁场中电流的连续性问题。
- 安培定律(磁场对其中的电流的作用力)和毕奥-萨法尔定律(两电流回路之间的作用力)
- 法拉第电磁感应定律——动磁生电
感应电流激发的磁场总是阻抗原磁通量的改变。(楞次定律)
- 真空中的麦克斯韦方程组
1)电场高斯定律(直接推广):电场(强度)的散度等于该处电荷体密度/电场的通量等于包围的电荷数(忽略常数因子)
2)磁场高斯定律(直接推广):磁场的散度/通量等于0,无散场
3)电磁感应定律(直接推广):感生电场的环量等于穿过这个环路包围面的磁通量的变化率(负值)
4)安培环路定理。 增加了一个位移电流。全电流等于磁场强度的旋度
- 电场和磁场的统一➪电磁场:电场与磁场可以脱离最初产生它们的电荷和电流而相互激发,时间上周而复始,空间上交链重复。电磁场的基本运动形态是波动——电磁波。
- 磁场对电流的作用力实质是对运动带电粒子的作用力。
电磁场对带电粒子的作用——洛伦兹力,是电场力与磁场力的和qE+qv×B。有时洛伦兹力也代指磁场力。
- 介质的分类:
☛线性介质:介质的极化、磁化和传导受到外加电磁场的影响,这种影响是线性的。
☛均匀介质:在空间中的分布是均匀的,即各点的电磁特性参数是常数。
均匀介质的一个特点是,极化电荷和磁化电流只存在于边界(表面),不存在于空间。
☛各向同性:电磁特性参数受外加电磁场的影响与外界电磁场的方向无关
☛色散介质:电磁特性参数随时间和/或空间变化的介质。这与另一种说法,即随频率变化,是一致的。
有些介质是空间色散,有些是时间色散。
- 极化和磁化
引入电位移矢![]() .只是一个辅助量,无物理意义。类似的也定义磁场强度H。
.只是一个辅助量,无物理意义。类似的也定义磁场强度H。![]()
束缚电荷(极化电荷)的和等于极化强度的相反数。如果引入P线,则其起始于极化负电荷,终止于极化正电荷。
变化的外加电磁场产生变化的极化强度,极化电流是极化强度的时间变化率。
类似有磁化强度(M)和磁化电流。
空间中任一点的电场是自由电荷和感应电荷共同的贡献。
- 介质中的麦克斯韦方程组:
先从方程本身进行描述:
介质中的高斯定理:对电位移矢量求散度就等于自由电荷体密度。
介质中的磁通连续定理和真空中一样:磁感应强度的散度等于零。
介质中的法拉第电磁感应定律:电场强度的旋度等于磁场时间变化率的负值。
介质中的安培环路定理:磁场强度的旋度等于电位移矢量的时间变化率与自由电流体密度的和。
再加上介质的3个本构方程,才是完备方程组。分别是电位移矢量与电场强度、电流密度与电场强度、磁感应强度与磁场强度。
总结一下,麦克斯韦方程组就是:电场有源、磁场无源;动电生磁、动磁生电。即:
电荷是电场通量源(电场高斯定理),
磁荷不存在(磁通连续定理)。
动磁生电(法拉第电磁感应)。
动电生磁(安培环路定理/全电流定律),表明位移电流和传导电流都可以产生磁场。
且这两个感应产生的场都是涡旋场。
如果把本构方程代入麦克斯韦方程组,则得到麦克斯韦方程组的限定形式。
- 边界条件
电场切向连续,磁场法向连续.电场法向的不连续度等于边界的(自由)面电荷密度,磁场切向的不连续度等于(自由)面电流密度。
边界处参数有突变,麦克斯韦的微分方程不适用,要用积分式。
- 理想介质:σ=0,无欧姆损耗的简单媒质。其自由电荷面密度与面电流密度都是0。
- 理想导体:δ=0,内部电场和磁场都为0,电荷和电流都只能在表面。
下面把第四章的内容直接合进来,因为第四章以计算为主,除此之外东西不多。而我这里主要总结思想和概念。
§4
- 静电场的唯一性定理保证了:解存在则正确,且唯一。
- 求解的三个方法:分离变量、格林函数、镜像法
格林函数前提是线性系统,思想是把电荷产生电位这件事等效成激励与响应的关系,并且是多个单位激励响应的线性叠加。格林函数可用于有源(Poisson方程)或无源区,分离变量只能用于无源区(Laplace方程)。镜像法是通过假想的点电荷等效感应电荷产生的贡献。
分离变量把偏微分方程拆成常微分(本征)方程。求解得到本征值和本征解系,含有的待定参数通过边界条件求出。
镜像法确定像电荷的思路:满足方程和边界条件、对称性、感应原理(与源电荷极性相反)
补充第一章一个恒等式:两次取旋等于求散后的梯度与拉普拉斯运算的差